2.6
1.蓝桥公园
2.路径
3.打印路径
4.【模板】Floyd
Floyd算法:
是一种多源的最短路径算法,经过一次计算可以得到任意两个点之间的最短路径。
这种算法是基于动态规划的思想:
m[i][j]表示从i到j这条边的距离,dp[k][i][j]表示从i到j且经过{0,1,...,k-1}中若干点的最短路径。
那么转移方程就就是dp[k][i][j]=min(dp[k−1][i][j],dp[k−1][i][k]+dp[k−1][k][j])这表示了比较经过k和不经过k两种的情况的路径,找到较小值

例如,在k=1的时候,
d p [ 1 ] [ i ] [ j ] = m i n ( d p [ 0 ] [ i ] [ j ] , d p [ 0 ] [ i ] [ 1 ] + d p [ 0 ] [ 1 ] [ j ] ) = m i n ( m [ i ] [ j ] , m [ i ] [ 1 ] + m [ 1 ] [ j ] ) 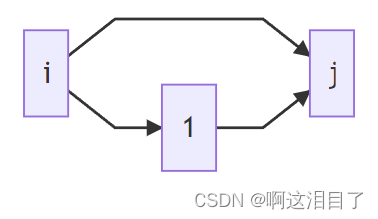
通过滚动数组,我们可以优化dp数组的空间,将他从三维的数组变成二维的
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])
与其他最短路径相比Floyd算法有以下几点特点:
1.可以找到所有节点之间的最短距离
2.代码简单,就三重循环
3.效率比较低,是O(n^3)的时间复杂度
这是算法的模版:
void floyd(){
for (int k=1;k<=n;++k){
for (int i=1;i<=n;++i){
for (int j=1;j<=n;++j){
if(i!=j)dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
else dp[i][j]=dp[j][i]=0;
}
}
}
}蓝桥公园:https://www.lanqiao.cn/problems/1121/learning/?page=1&first_category_id=1&status=2
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
const int INF=0x3f3f3f3f3f3f3f3fll;
const int N=405;
int dp[N][N];
int n,m,q;
void input(){
memset(dp,0x3f,sizeof(dp));
for (int i=1;i<=m;++i){
int u,v,w;
cin>>u>>v>>w;
dp[u][v]=dp[v][u]=min(dp[u][v],w);
}
}
void fioyd(){
for (int k=1;k<=n;++k){
for (int i=1;i<=n;++i){
for (int j=1;j<=n;++j){
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
}
}
}
}
void output(){
while (q--){
int s,t; cin>>s>>t;
if (s==t) cout<<0<<endl;
else if (dp[s][t]==INF) cout<<-1<<endl;
else cout<<dp[s][t]<<endl;
}
}
signed main(){
cin>>n>>m>>q;
input(); fioyd(); output();
return 0;
}
路径:https://www.lanqiao.cn/problems/1460/learning/?page=1&first_category_id=1&problem_id=1460
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
const int INF=0x3f3f3f3f;
const int N=2050;
int dp[N][N];
int gcd(int a,int b){
if (b==0) return a;
return gcd(b,a%b);
}
void floyd(){
for (int k=1;k<=2021;++k){
for (int i=1;i<=2021;++i){
for (int j=1;j<=2021;++j){
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
}
}
}
}
signed main(){
for (int i=1;i<2021;++i){
for (int j=i+1;j<=2021;++j){
if (abs(i-j)>21){
dp[i][j]=dp[j][i]=INF;
}else if (abs(i-j)<=21){
dp[i][j]=dp[j][i]=(i*j)/gcd(i,j);
}
}
}
floyd();
cout<<dp[1][2021];
}
打印路径:https://www.lanqiao.cn/problems/1656/learning/?page=1&first_category_id=1&problem_id=1656
这道题需要的点比较多,需要记录最短路径,还有每个 城市都会收税,记录最短路径的话,就再建一个二维数组,记录每个点之间的关系
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
const int INF=0x3f3f3f3f;
const int N=505;
int n;
int dp[N][N],shui[N],path[N][N];
void input(){
cin>>n;
for (int i=1;i<=n;++i){
for (int j=1;j<=n;++j){
int x; cin>>x;
if (x==-1) dp[i][j]=dp[j][i]=INF;
else{
dp[i][j]=dp[j][i]=x;
}
path[i][j]=j;
}
}
for (int i=1;i<=n;++i) cin>>shui[i];
}
void floyd(){
for (int k=1;k<=n;++k){
for (int i=1;i<=n;++i){
for (int j=1;j<=n;++j){
if (dp[i][j]>dp[i][k]+dp[k][j]+shui[k]){
dp[i][j]=dp[i][k]+dp[k][j]+shui[k];
path[i][j]=path[i][k];
}else if (dp[i][k]+dp[k][j]+shui[k]==dp[i][j] && path[i][k]<path[i][j]){
dp[i][j]=dp[i][k]+dp[k][j]+shui[k];
path[i][j]=path[i][k];
}
}
}
}
}
void output(){
int s,t;
while (cin>>s>>t){
if (s==-1 && t==-1)break;
cout<<"From "<<s<<" to "<<t<<" :"<<endl;
cout<<"Path: "<<s;
int idx=s;
while (idx!=t){
idx=path[idx][t];
cout<<"-->"<<idx;
}
cout<<endl;
cout<<"Total cost : "<<dp[s][t]<<endl<<endl;
}
}
signed main(){
input(); floyd(); output();
return 0;
}
【模板】Floydhttps://www.luogu.com.cn/problem/B3647
题目描述
给出一张由 �n 个点 �m 条边组成的无向图。
求出所有点对 (�,�)(i,j) 之间的最短路径。
输入格式
第一行为两个整数 �,�n,m,分别代表点的个数和边的条数。
接下来 �m 行,每行三个整数 �,�,�u,v,w,代表 �,�u,v 之间存在一条边权为 �w 的边。
输出格式
输出 �n 行每行 �n 个整数。
第 �i 行的第 �j 个整数代表从 �i 到 �j 的最短路径。
输入输出样例
输入 #1复制
4 4 1 2 1 2 3 1 3 4 1 4 1 1
输出 #1复制
0 1 2 1 1 0 1 2 2 1 0 1 1 2 1 0
说明/提示
对于 100%100% 的数据,�≤100n≤100,�≤4500m≤4500,任意一条边的权值 �w 是正整数且 1⩽�⩽10001⩽w⩽1000。
数据中可能存在重边。
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
const int INF=0x3f3f3f3f;
const int N=505;
int n,m;
int dp[N][N];
void floyd(){
for (int k=1;k<=n;++k){
for (int i=1;i<=n;++i){
for (int j=1;j<=n;++j){
if(i!=j)dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
else dp[i][j]=dp[j][i]=0;
}
}
}
}
signed main(){
cin>>n>>m;
memset(dp,INF,sizeof(dp));
for (int i=1;i<=m;++i){
int a,b,c;
cin>>a>>b>>c;
dp[a][b]=dp[b][a]=min(dp[a][b],c); //防止重边
}
floyd();
for (int i=1;i<=n;++i){
for (int j=1;j<=n;++j){
cout<<dp[i][j]<<" ";
}
cout<<endl;
}
return 0;
}