概念

搜索二叉树是一种特殊的二叉树，其具有以下特点：

1.对于每个结点，它的左子树中的所有节点的值都小于该节点的值，而右子树中的所有节点的值都大于该节点的值。
2.左子树和右子树都是搜索二叉树。

这个 特性使得搜索二叉树可以用于高效地进行查找、插入和删除操作。通过利用节点之间的大小关系，我们可以快速定位到目标值所在的位置，避免不必要的比较操作。

在数据结构专栏已经讲解过了二叉树了：

二叉树1
二叉树2

下面直接讲解对搜索二叉树的实现。

实现搜索二叉树

二叉树结点模板

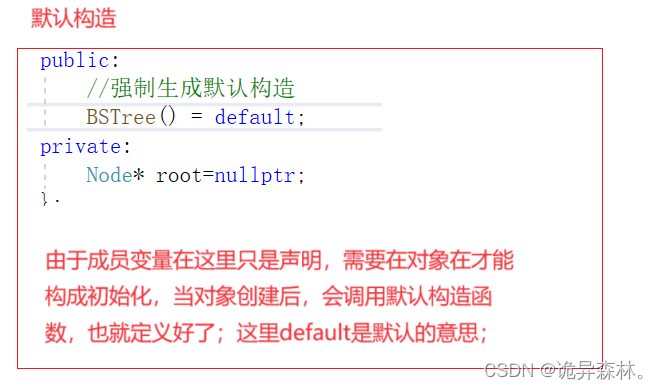
默认构造

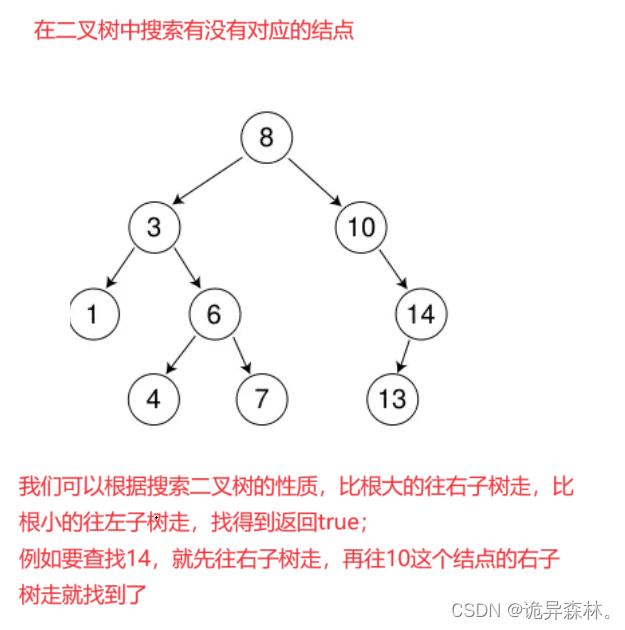
查找

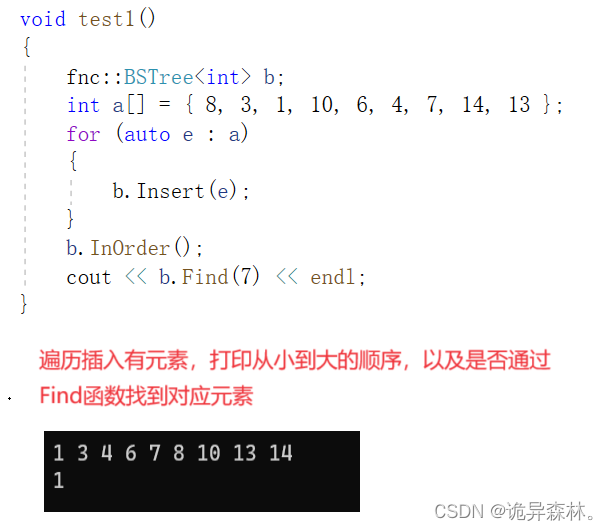
插入

bool Insert(const K& key)
		{
			if (_root == nullptr)
			{
				_root = new Node(key);
				return true;
			}

			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (key > cur->_key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}

			cur = new Node(key);
			if (key > parent->_key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}

			return true;
		}

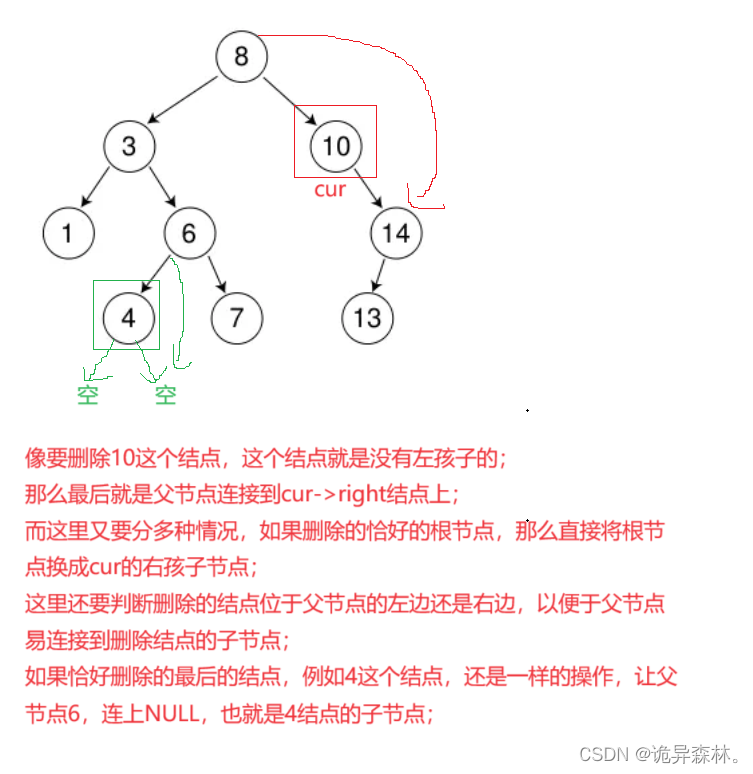
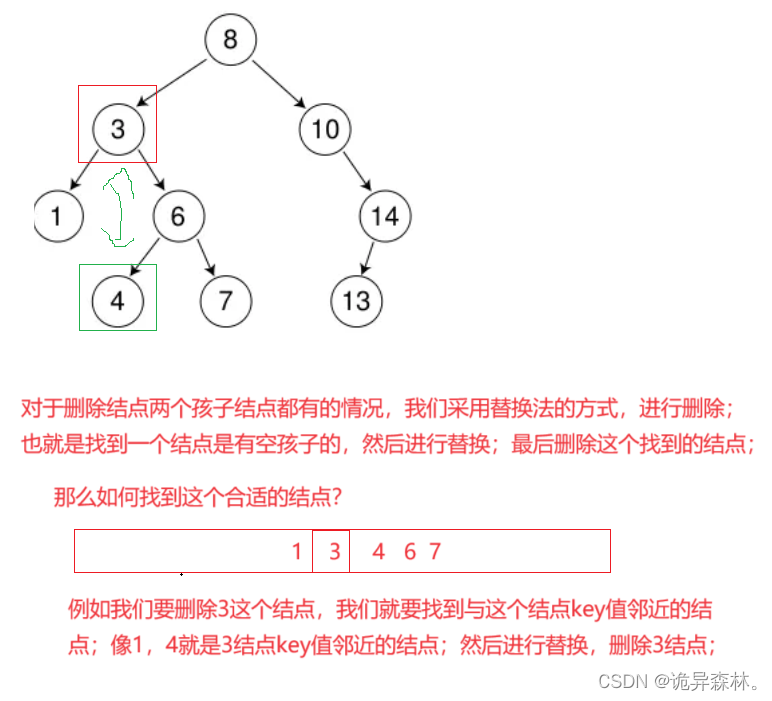
删除

bool Erase(const K& key)
		{
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (key > cur->_key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					if (cur->_left == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (cur == parent->_right)
							{
								parent->_right = cur->_right;
							}
							else
							{
								parent->_left = cur->_right;
							}
						}
						delete cur;
						return true;
					}
					else if (cur->_right == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_left;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
						return true;

					}
					else
					{
						Node* rightMinParent = cur;
						Node* rightMin = cur->_right;
						while (rightMin->_left)
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}

						cur->_key = rightMin->_key;
						if (rightMin == rightMinParent->_left)
						{
							rightMinParent->_left = rightMin->_right;
						}
						else
						{
							rightMinParent->_right = rightMin->_right;
						}
						delete rightMin;
						return true;
					}
				}
			}
			return false;
		}

拷贝、赋值、析构

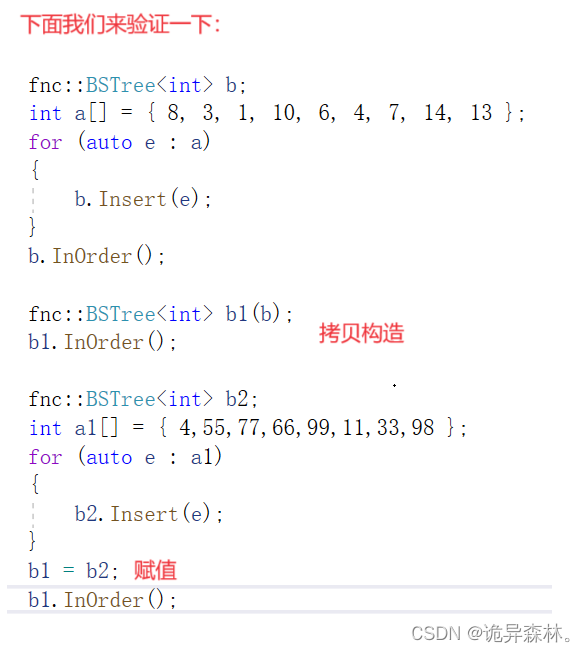
递归版本的增删查

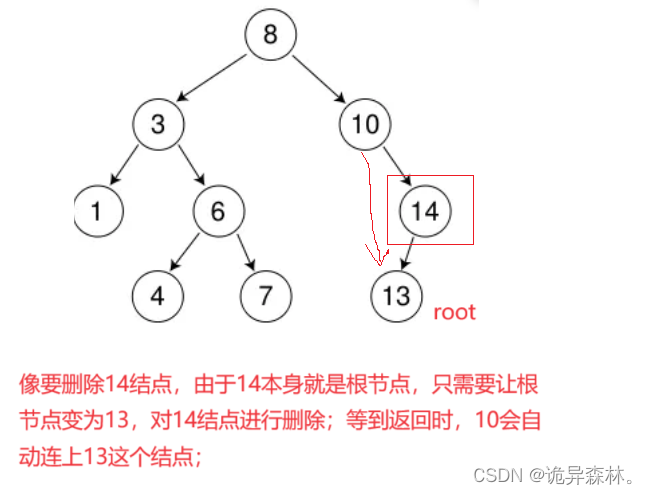
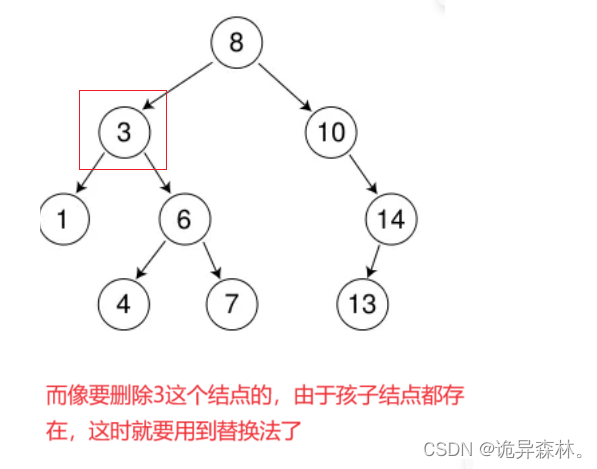
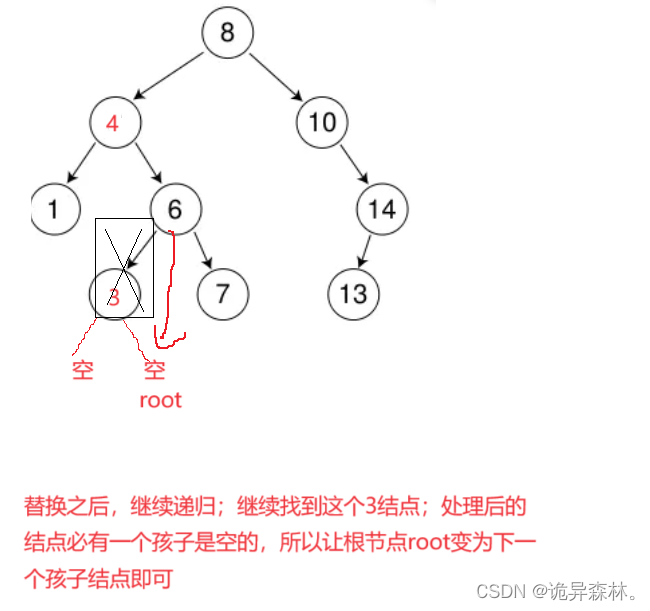
删除：

bool _EraseR(Node*& root,const K& key)
		{
			if (root == nullptr)
				return false;

			if (root->_key < key)
				return _EraseR(root->_right, key);
			else if (root->_key > key)
				return _EraseR(root->_left, key);
			else
			{
				Node* del = root;
				if (root->_right == nullptr)
					root = root->_left;
				else if (root->_left == nullptr)
					root = root->_right;
				else
				{
					Node* rightMin = root->_right;
					while (rightMin->_left)
						rightMin = rightMin->_left;
					swap(root->_key, rightMin->_key);
					return _EraseR(root->_right, key);
				}
				delete del;
				return true;
			}
		}

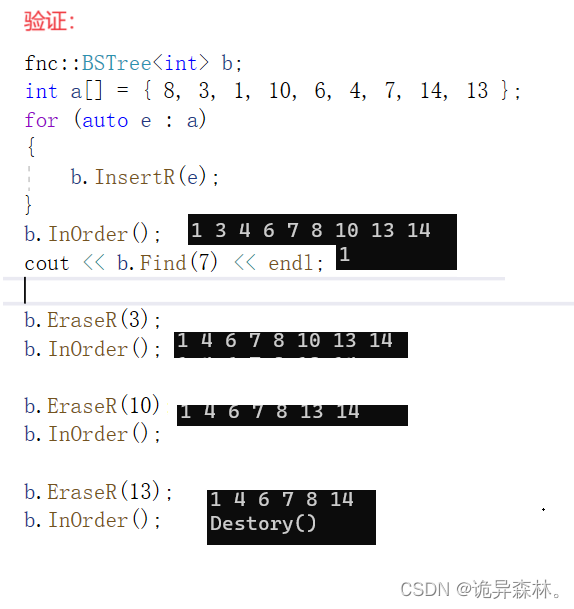
实现源码

#pragma once

namespace fnc
{
	template<class K>
	struct BSTreeNode
	{
		typedef BSTreeNode<K> Node;

		Node* _left;
		Node* _right;
		K _key;

		BSTreeNode(const K& key)
			:_left(nullptr),
			_right(nullptr),
			_key(key)
		{}
	};

	template<class K>
	class BSTree
	{
		typedef BSTreeNode<K> Node;
	public:
		//强制生成默认构造
		BSTree() = default;
		//拷贝构造
		BSTree(const BSTree<K>& t)
		{
			_root = Copy(t._root);
		}
		//赋值
		BSTree<K>& operator=(BSTree<K> t)
		{
			swap(_root, t._root);
			return *this;
		}
		//析构
		~BSTree()
		{
			Destory(_root);
			cout << "Destory()" << endl;
		}
		//查找
		bool Find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else
				{
					return true;
				}
			}
			return false;
		}

		//插入
		bool Insert(const K& key)
		{
			if (_root == nullptr)
			{
				_root = new Node(key);
				return true;
			}

			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (key > cur->_key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}

			cur = new Node(key);
			if (key > parent->_key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}

			return true;
		}
		bool Erase(const K& key)
		{
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (key > cur->_key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					if (cur->_left == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (cur == parent->_right)
							{
								parent->_right = cur->_right;
							}
							else
							{
								parent->_left = cur->_right;
							}
						}
						delete cur;
						return true;
					}
					else if (cur->_right == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_left;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
						return true;

					}
					else
					{
						Node* rightMinParent = cur;
						Node* rightMin = cur->_right;
						while (rightMin->_left)
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}

						cur->_key = rightMin->_key;
						if (rightMin == rightMinParent->_left)
						{
							rightMinParent->_left = rightMin->_right;
						}
						else
						{
							rightMinParent->_right = rightMin->_right;
						}
						delete rightMin;
						return true;
					}
				}
			}
			return false;
		}
		//打印
		void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}


		

		bool FindR(const K& key)
		{
			return _FindR(_root, key);
		}
		bool InsertR(const K& key)
		{
			return _InsertR(_root, key);
		}
		bool EraseR(const K& key)
		{
			return _EraseR(_root, key);
		}

	private:
		bool _EraseR(Node*& root,const K& key)
		{
			if (root == nullptr)
				return false;

			if (root->_key < key)
				return _EraseR(root->_right, key);
			else if (root->_key > key)
				return _EraseR(root->_left, key);
			else
			{
				Node* del = root;
				if (root->_right == nullptr)
					root = root->_left;
				else if (root->_left == nullptr)
					root = root->_right;
				else
				{
					Node* rightMin = root->_right;
					while (rightMin->_left)
						rightMin = rightMin->_left;
					swap(root->_key, rightMin->_key);
					return _EraseR(root->_right, key);
				}
				delete del;
				return true;
			}
		}
		bool _InsertR(Node*& root, const K& key)
		{
			if (root == nullptr)
			{
				root = new Node(key);
				return true;
			}
			if (key > root->_key)
			{
				return _InsertR(root->_right, key);
			}
			else if (key < root->_key)
			{
				return _InsertR(root->_left, key);
			}
			else
			{
				return false;
			}
		}
		bool _FindR(Node* root, const K& key)
		{
			if (root == nullptr)
			{
				return false;
			}
			if (root->_key < key)
			{
				return _FindR(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _FindR(root->_left, key);
			}
			else
			{
				return true;
			}
		
		}

		void Destory(Node* root)
		{
			if (root == nullptr)
				return;

			Destory(root->_left);
			Destory(root->_right);
			delete root;
		}
		Node* Copy(Node* root)
		{
			if (root == nullptr)
			{
				return nullptr;
			}
			Node* newRoot = new Node(root->_key);
			newRoot->_left = Copy(root->_left);
			newRoot->_right = Copy(root->_right);
			return newRoot;
		}
		void _InOrder(Node* root)
		{
			if (root == nullptr)
			{
				return;
			}
			_InOrder(root->_left);
			cout << root->_key << " ";
			_InOrder(root->_right);
		}
	private:
		Node* _root=nullptr;
	};
}