Manacher算法

https://github.com/SongJianHIT/DataStructurs-Algorithm/tree/main/src/algorithms/manacher

基本介绍

Manacher 算法常用于 求一个字符串中的最长回文子串。如：abc123321def 的最长回文子串为 123321。

计算字符串的最长回文字串最简单的算法就是枚举该字符串的每一个子串，并且判断这个子串是否为回文串，这个算法的时间复杂度为 $O(N^3)$ 的。Manacher 算法可以在 线性时间复杂度 $O(N)$ 内求出一个字符串的最长回文字串，达到了理论上的下界。

Manacher 算法原理与实现

首先，Manacher 算法提供了一种巧妙的办法，将长度为奇数的回文串和长度为偶数的回文串一起考虑，具体做法是，在原字符串的每个相邻两个字符中间插入一个分隔符，同时在首尾也要添加一个分隔符，分隔符的要求是不在原串中出现，一般情况下可以用 # 号。如：

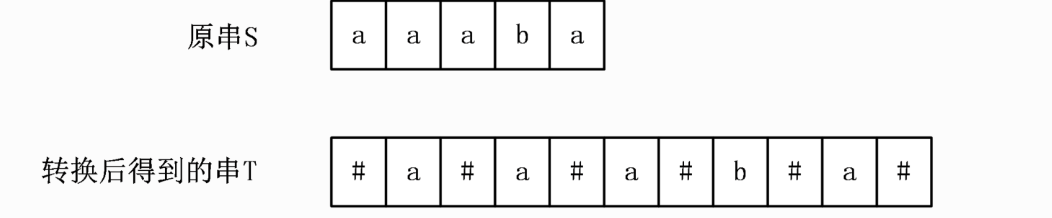
概念：回文直径与回文半径

举个例子，如字符串 abc12321def 的回文子串为 12321，因此回文直径为 5，回文半径为 3；又如字符串 1221，回文直径为 4，回文半径为 2。

概念：回文半径数组 pArr

原始串再添加了特殊字符 # 后，得到处理串。

我们在处理串上，对每个字符 T[i]，记录以 T[i] 为中心的最长回文字串的最右字符到 T[i] 的长度**（回文半径）**。比如以 T[i] 为中心的最长回文字串是 T[l,r]，那么 Len[i]=r-i+1。

概念：最右回文边界 R

最右回文边界是一个 int 类型整数。初始值 int R = -1;。他的含义是，不管是从哪个位置 i 作为中心点向左右两边扩，只要扩出来的回文区域的右边界更靠右了，就更新 R。

概念：取得最右回文右边界的中心 C

取得最右回文右边界的中心是一个 int 类型整数。初始值 int C = -1;。R 只要更新，C 就负责记录是哪个中心点扩的时候让 R 更新了。

对上述概念举个例子：

算法流程

Manacher 算法从 index=0 开始，以 str'[index] 为中心，向左右两边扩，找最长回文子串。

当 index=i 时，有如下几种情况：

1. i 没有被 R 扩住，即 i > R

   此时，无法优化，暴力扩就行了。

2. i 被 R 扩住，即 i <= R

   此时存在这种拓扑关系 [L i' C i R]，i' 是 i 关于 C 的对称点。比较特殊的是 i 与 R 重叠，但讨论一样。

   接下来，分类讨论：

   • 情况 1：i' 扩出来的区域彻底在 [L, R] 内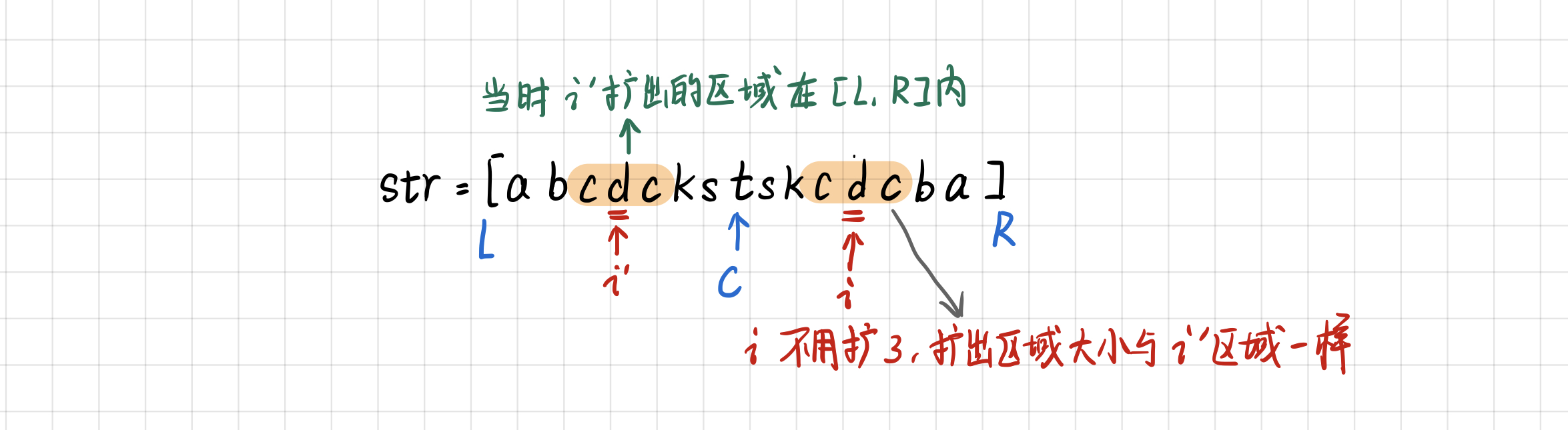

     

     此时，i 不用扩了，i 的回文区域大小与 i' 一样大。

   • 情况 2：i' 扩出来的区域跑到 [L, R] 外面了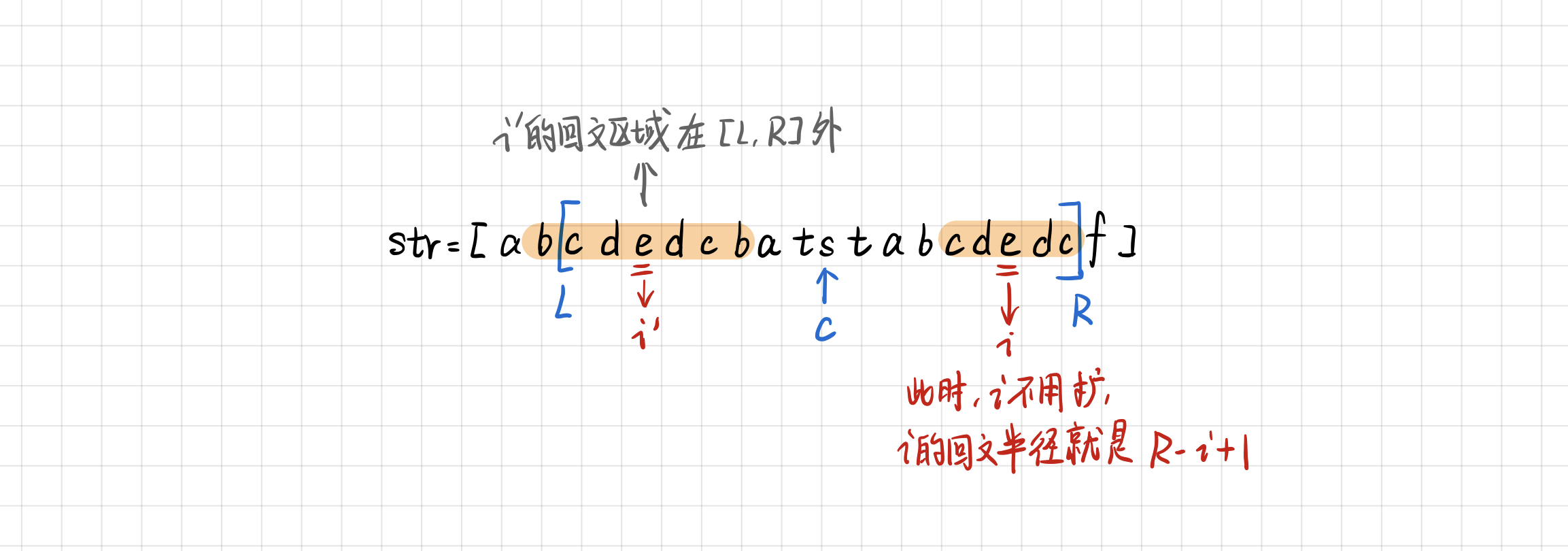

     

     此时，i 不用扩了，i 的回文区域只会到 R，回文半径可计算为 R - i + 1。

   • 情况 3：i' 的左边界与回文区域重合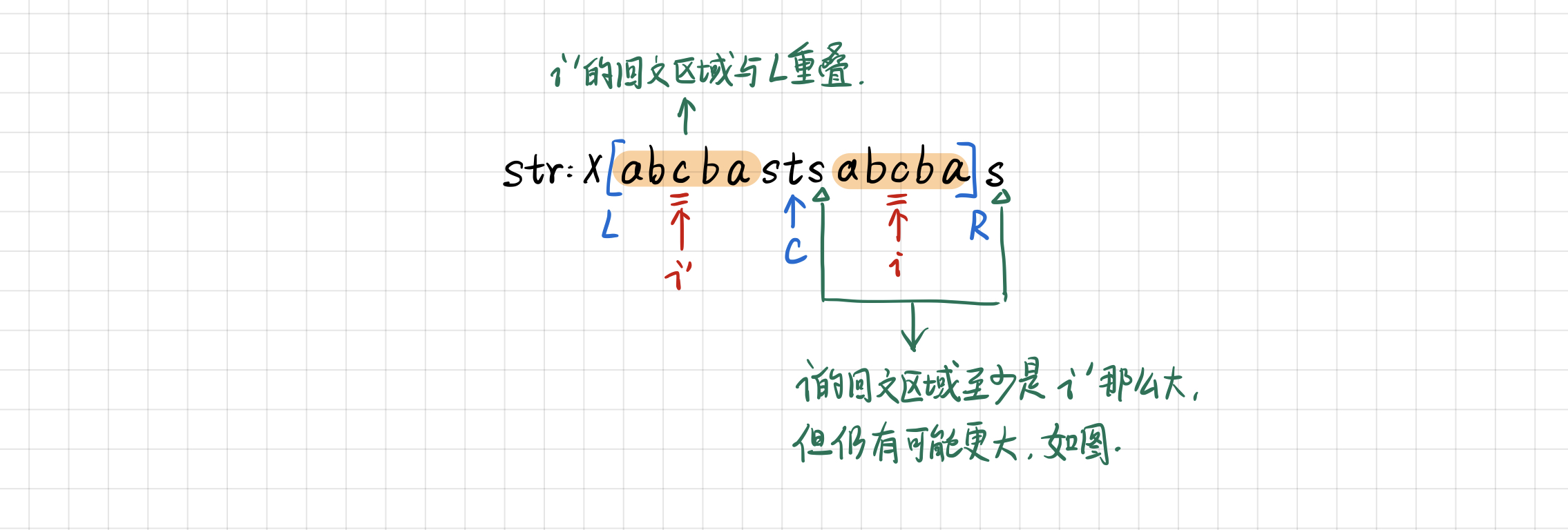

     

     此时，i 的回文区域至少是 i' 那么大，但还有可能更大！

经典题目

题目一：最少添加多少字符变成回文串

在一个字符串中，只能够在字符串的后面添加字符，最少需要添加多少个字符，使其能够变成回文串。

如：str=[abc12321]，要使其变成回文串，最少需要 3 个字符 [cba]。

解决方法

这道题实际上是在求，必须包括最后一个字符的情况下，最长回文子串是多长，长度记为 x。字符串总长度为 len，要使其变为回文串，则最少需要 len - x 个字符即可。

只要找到 必须包括最后一个字符的情况下，最长回文子串是多长 后，把前面的字符串逆序即可。

怎么找呢？

• 每个 index 都推出一个右边界，当右边界到达最后一个字符串时，停！就找到此时的中心 C，这就是最长回文串的中心。