目录

💥1 概述

📚2 运行结果

🎉3 参考文献

👨‍💻4 Matlab代码

---

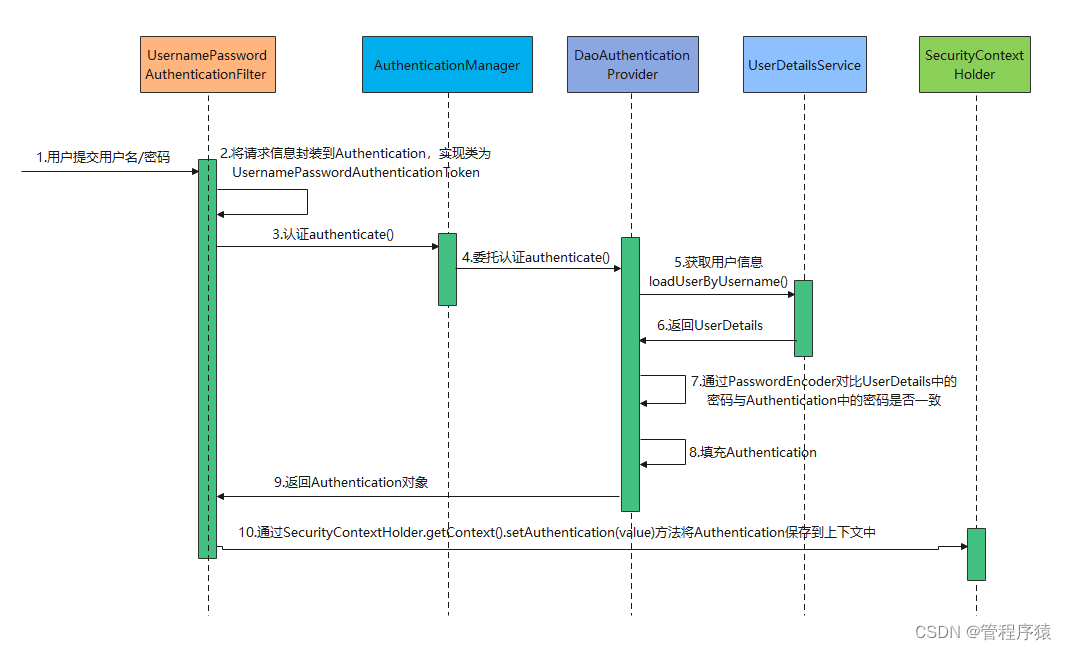
💥1 概述

灵敏度分析分为局部灵敏度分析和全局灵敏度分析；局部灵敏度分析包括：直接求导法、有限差分法、格林函数法。全局灵敏度分析算法有筛选法、蒙特卡洛方法、基于方差的方法。筛选法主要有IFFD、MOAT、COTTER法等，一般用于分析包含大量输入变量的系统模型、计算量相对较小。蒙塔卡罗方法是一种主要基于统计学理论的方法，包括散点图法、相关系数法、回归分析法等，对于线性单调模型分析具有较强的适用性。基于方差的方法是近年来研究较多且应用最广的一类方法，主要有重要性估计法、傅里叶幅值灵敏度测试法（FAST）、以及拓展傅里叶幅值灵敏度检验方法（EFAST）等。SOBOL全局灵敏度分析法同时具备了蒙塔卡罗法和方差法的特点。

📚2 运行结果

🎉3 参考文献

[1]吴庶宸,戚宗锋,李建勋.基于深度学习的智能全局灵敏度分析[J].上海交通大学学报,2022,56(07):840-849.DOI:10.16183/j.cnki.jsjtu.2021.191.

👨‍💻4 Matlab代码

主函数部分代码：

clear;

% Ishigami-Homma function
f = @(x,p) sin(x(1)) + p.a * sin(x(2)^2) + p.b * x(3)^4 * sin(x(1));
p.a = 2; p.b = 1;
ih = @(x) f(x, p);

% Bounds
lb = ones(1,3) * -pi; ub = ones(1,3) * pi;

% Parameters from Figure 4's caption
n=15;
Nu = 100;
Nc = 100; % Is actually 50 in the paper

% Other parameters
npts = 100; seed = 4;

[KS,xvals,y_u, y_c, par_u, par_c, ft] = PAWN(f, p, lb, ub, Nu, n, Nc, npts, seed);

m1 = min([y_c, y_u']);
m2 = max([y_c, y_u']);
[f,ci] = ksdensity(y_u, linspace(m1,m2,npts), 'Function', 'cdf');

% Begin Plotting
subplot(331); ylabel('y'); hold on;box on;
subplot(334); ylabel('CDF'); hold on;  box on;
subplot(337); ylabel('KS'); hold on; xlabel('x_1'); box on;
subplot(338); xlabel('x_2'); hold on;box on;
subplot(339); xlabel('x_3'); hold on;box on;
for ind=1:length(lb)
    subplot(330+ind)
    plot(par_c(:,ind),y_c, 'xk', 'markersize', 2);
end

crit_c = [1.22,1.36,1.48,1.63,1.73,1.95]; % 0.1, 0.05, 0.025, 0.010, 0.005, 0.001
critval = crit_c(2) * sqrt((Nu+Nc)/(Nu*Nc));

for ind=1:length(lb)
    subplot(333+ind)
    plot([-100, 100], [1, 1], 'k--'); hold on
    plot(ci,ft((ind-1)*n+1:ind*n,:), 'color', [0.8,0.8,0.8]); ylim([0,1]);
    plot(ci,f, 'r:','linewidth',4); ylim([0,1.2])
    hold off
end

colData = linspace(0,n,n)'/n; colData = [colData colData colData];

for ind=1:length(lb)
    subplot(336+ind)
    [xtoplot, indices] = sort(xvals(ind,:));
    ytoplot = KS(ind, :); ytoplot = ytoplot(indices);
    plot([min(xvals(:)), max(xvals(:))], [critval,critval], 'k--'); hold on;
    plot(xtoplot, ytoplot, 'k');
    scatter(xtoplot, ytoplot, [],  colData, 'filled', 'markeredgecolor', 'k'); 
    ylim([0,1])
    hold off
end