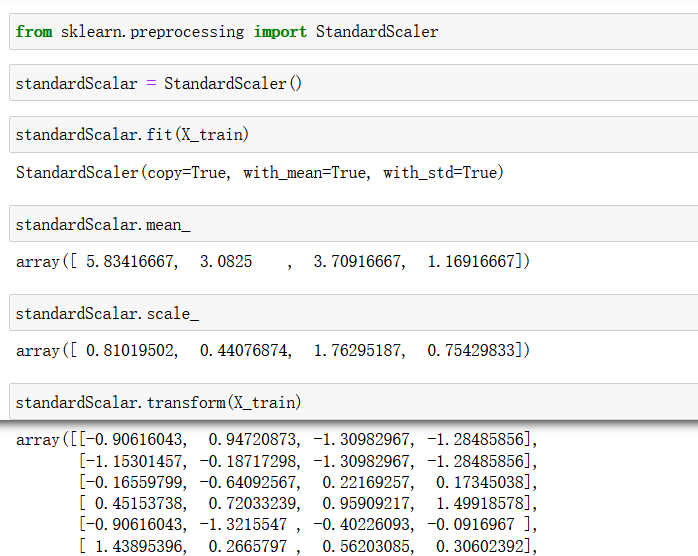
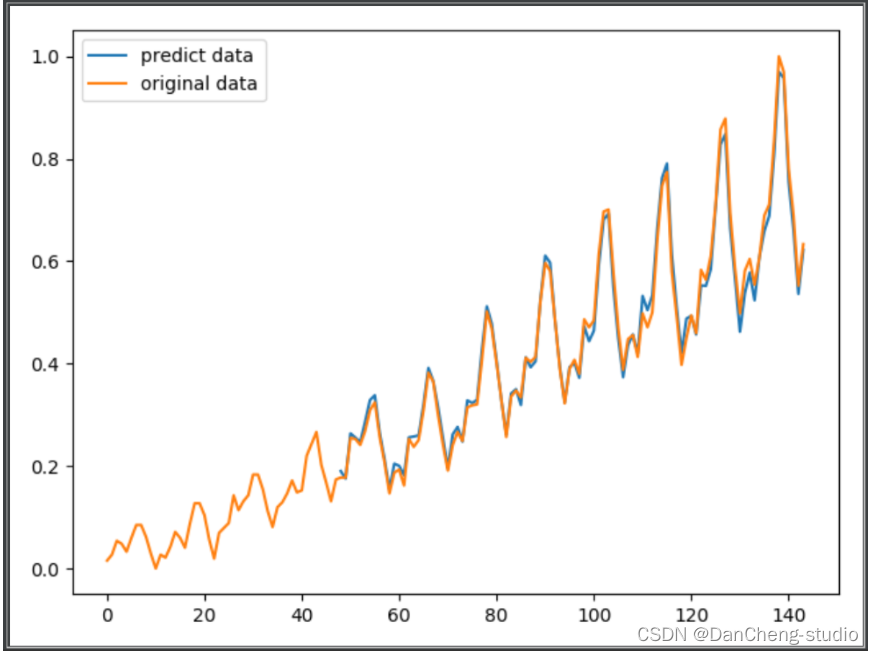
假设表达式中允许包含两种括号：圆括号和方括号，嵌套顺序要求：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

考虑下列括号序列：

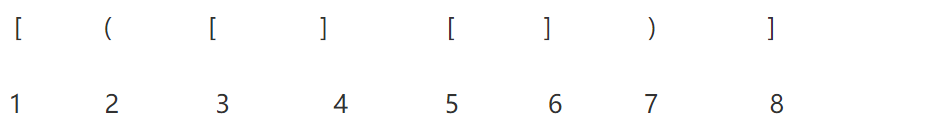
分析如下：

1. 计算机接收到第一个‘[’后，期待与之匹配的第八个‘]’的出现
2. 获得了第二个‘(’，此时第一个‘[’暂时先放到一边，并期待着与之匹配的第七个‘)’出现
3. 获得了第三个‘[’后，此时第二个先暂时放到一边，并期待与之匹配的第四个‘]’出现
4. 第四个出现后，第三个的期待得到满足，消解之后，第二个‘(’的期待又称为当前的当务之急
5. 以此类推……

思想如下：

1. 创建一个空栈，顺序读入括号
2. 如果是左括号，则作为一个新的更急迫的期待压入栈中，自然使得原有的栈中所有未消解的期待的急迫性降了一级
3. 如果是右括号，则要么使置于栈顶的最急迫的期待得到满足，要么是不合法的情况（括号序列不匹配，退出程序）
4. 算法结束时，栈为空；否则括号序列不匹配

bool bracketCheck(char str[],int length){
	SqStack S;
	InitStack(S);

	for(int i=0;i<length;i++){
		if(str[i]=='('||str[i]=='['||str[i]=='{'){
			Push(S,str[i]);//扫描到左括号，入栈
		}else{
			if(isEmpty(S)){
				return false;//如果此时栈空了，却匹配到了右括号
			}
			//如果栈非空
			char topElem;//栈顶元素
			Pop(S,topElem);//获取栈顶元素
			if(str[i]==')'&&topElem!='('){
				return false;
			}
			if(str[i]=='['&&topElem!=']'){
				return false;
			}
			if(str[i]=='{'&&topElem!='}'){
				return false;
			}
		}
	}
	return isEmpty(S);//如果最后栈中非空，说明还有左括号没有得到匹配
}