创建时间：2024-02-02
最后编辑时间：2024-02-03
作者：Geeker_LStar

你好呀~这里是 Geeker_LStar 的人工智能学习专栏，很高兴遇见你~
我是 Geeker_LStar，一名初三学生，热爱计算机和数学，我们一起加油~！
⭐(●’◡’●) ⭐
那就让我们开始吧！

上一篇【初中生讲机器学习】3. 支持向量机（SVM）一万字详解！超全超详细超易懂！当中，我们已经详细了解了支持向量机算法以及它背后的数学原理，但是上一篇文章中没有给出实例代码，so 这一篇主要就通过一个实例来看看支持向量机算法应该怎么实现，有哪些要点~

完整代码见文末~

实例：利用支持向量机对鸢尾花进行分类。
（神奇，我这学期的作文里貌似三次写到鸢尾花诶）

话不多说，首先，我们导入各种需要的库（or 需要的函数方法 or 数据集）。

'''第一步，导入各种需要的库'''
import matplotlib.pyplot as plt    # 用于数据可视化
import matplotlib as mpl
from sklearn import svm    # 引入封装好的 SVM 算法
from sklearn.datasets import load_iris    # 引入鸢尾花数据集，共 150 组数据
from sklearn.model_selection import train_test_split    # 划分训练集和测试集的函数方法
from sklearn.metrics import accuracy_score    # 评判测试准确度的函数方法
import numpy as np    # 进行科学计算

matplotlib，进行数据可视化的库。
numpy 用于进行科学计算。
scikit learn，即 sklearn 库，是机器学习中非常重要的一个库，它封装了大量常用算法，如分类、回归、降维、聚类等，并且提供一些常用数据集，其中就包括本例中用到的鸢尾花数据集。

接着，我们需要对鸢尾花数据集有一个了解，先加载它，然后输出一些它的特征。

iris = load_iris()    # 加载数据集
print(iris.target)    # 数据标签（分类结果标签）
print(iris.target_names)    # 三种鸢尾花的名字
print(iris.feature_names)    # 四个分类特征的名字

这是输出结果，可以看到，数据集中的鸢尾花一共有三类 150 个，每一类有 50 个。分类标准是【萼片长度】【萼片宽度】【花瓣长度】【花瓣宽度】。

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
['setosa' 'versicolor' 'virginica']
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

再来看一下每一个鸢尾花数据是怎么表示的（没错其实就是四维向量，因为四个特征嘛），以及它们对应的数据标签。

X = iris.data    # 输入数据（150 个四维向量），样本特征，[n_samples * n_features] 的二维数组
print(X.shape, X)    # X.shape，输出 X 数组的行数和列数
y = iris.target    # 数据标签 or 分类结果（共三种每种 50 个数据）
print(y.shape, y)

输出如下（一部分），大意是：输入数据一共 150 个，每个都是一个四维向量，对应的数据标签是 0 或 1 或 2。

(150, 4) [[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]

(150,) [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

哦？这样不够直观？看不出这 150 组数据在分布上有什么特点？没事，咱有 matplotlib，画个图嘛！
errr，我们分别以前两个特征（萼片长宽）和后两个特征（花瓣长宽）为特征画图。画完图其实可以看出一些东西，不过这里先不透露。

# 以前两个特征（花萼长度、花萼宽度）绘图
X = iris.data[:, :2]    # 切片操作，选取前两个特征
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "red", marker = "o")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "green", marker = "+")
plt.scatter(X[y == 2, 0], X[y == 2, 1], color = "blue", marker = "x")
plt.xlabel('sepal length', fontsize=20)
plt.ylabel('sepal width', fontsize=20)
plt.title('Iris names', fontsize=30)
plt.show()

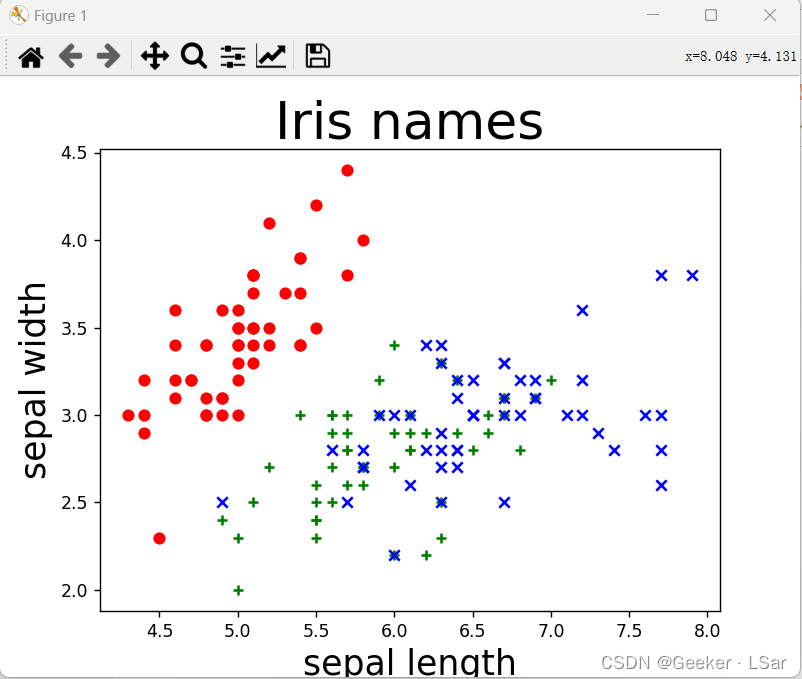
这是这些鸢尾花的萼片长宽的分布图，不难发现，通过萼片长宽可以比较好的将第一种鸢尾花（红色）和第二三种（绿/蓝色）区分开，但是第二种和第三种之间却不太好区分。

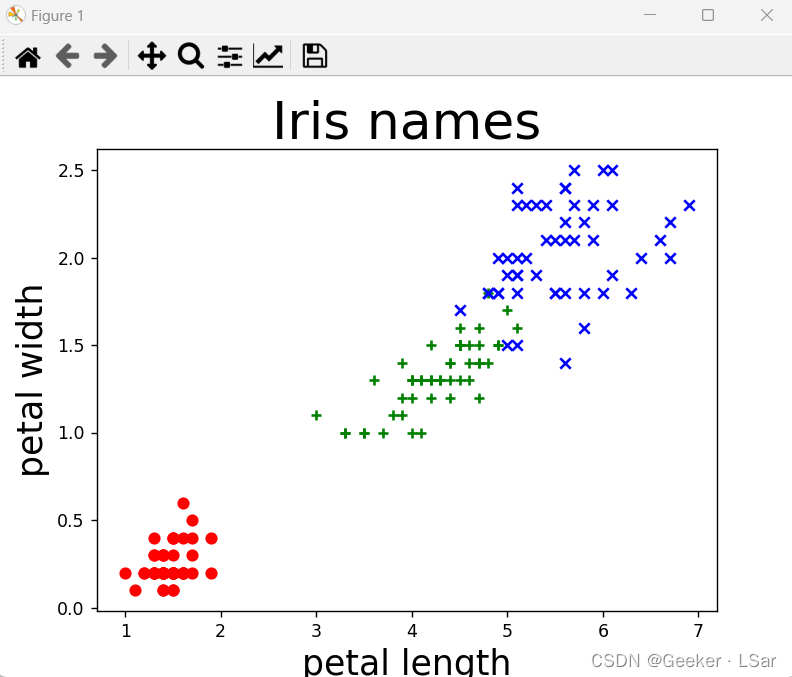
再来看看花瓣长宽的情况。

# 以后两个特征（花瓣长度、花瓣宽度）绘图（发现后两个特征能够更好地区分三类鸢尾花）
X = iris.data[:, 2:]
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "red", marker = "o")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "green", marker = "+")
plt.scatter(X[y == 2, 0], X[y == 2, 1], color = "blue", marker = "x")
plt.xlabel('petal length', fontsize=20)
plt.ylabel('petal width', fontsize=20)
plt.title('Iris names', fontsize=30)
plt.show()

分布图长这样，不难看出，可以通过花瓣长宽特征将三种鸢尾花大致分开，【只按照花瓣特征分】比【只按照萼片特征分】的效果更好（为什么提到这个，因为后面要写相关代码~）。

ok，现在我们对整个数据集已经有了大致的了解，可以利用支持向量机来分类啦！

通常来讲，用 SVM 分类可以按照这个顺序进行，其中 2、3 可以反过来：

1. 获取所需数据集（全部特征 or 某个或某几个特征（切片））
2. 定义支持向量机（svm.SVC()）
3. 划分训练集和测试集（train_test_split()）
4. 利用训练集进行训练（fit()）
5. 测试，预测测试集的输出结果（predict()）
6. 计算测试准确率并输出，模型评价（accuracy_score()）
7. 绘制结果（如果需要）

那我们就按照这个步骤来吧！先来最简单的，用全部特征进行分类，先训练再测试。

第一步，获取所需数据集，这两行代码的意思上面已经解释过：

X = iris.data
y = iris.target

第二步，定义支持向量机，解释一下其中的一些参数，这些参数的详细讲解都在上一篇：

• kernel：核函数类型，“linear” 表示线性核函数，“poly” 表示多项式核函数，“rbf” 表示高斯核函数（径向基函数）。
• C：惩罚项，默认值为 1。C 的值很关键，过小会导致模型的泛化能力弱（过拟合），过大又会导致欠拟合。
• gamma：核函数的核系数，一般情况下默认为 1/n_features。
• probability：是否支持输出样本属于不同类的概率，True 表示支持。

svm1 = svm.SVC(kernel="rbf", C=1, gamma="auto", probability=True)

第三步，划分训练集和测试集：
train_test_split() 用于划分训练集和测试集，其中，test_size 指测试集数据量占数据总量的百分比，0.3 即有 30% 的数据用于测试，其余数据用于训练；random_state 是随机数种子，改变它可以获得不同的数据划分，通常在交叉验证中使用。

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=218)

第四步，利用训练集进行训练：
fit() 方法，用于训练支持向量机，也就是拟合。

svm2.fit(X_train, y_train)

第五步，测试，预测测试集的输出结果：
训练完 SVM，就让它去预测一下测试集的数据吧。
predict() 函数用于预测。

y_predict = svm2.predict(X_test)

第六步，计算测试准确率并输出，也就是模型评价：
accuracy_score() 函数计算模型预测的准确率，是评价模型性能的一项参考指标，与之类似的参考指标还有召回率、ROC 曲线、AUC 值等，这些在第二篇中讲过~（sklearn 库也提供其他参考指标的函数方法，但是本例中用不到）。

print("准确率：", accuracy_score(y_test, y_predict))

ok！此时一个 SVM 的训练+测试就完成了！我这里的准确率是 95.6%。

如果对准确率不满意，可以尝试调整惩罚系数 C，也可以尝试换一种核函数，或者提高训练集的占比使模型得到更充分的训练，等等。

ok，走了一遍基础流程，其实 SVM 的训练并不难的（）下面我们来看看如果我们想按照某些特征进行分类（比如之前提到的按照萼片长宽分类），并且想更直观地看到这个超平面是怎么划分的，我们应该怎么做。

其实大体上没什么变化，只不过在获取数据的时候需要做一个切片处理，语法和 Python 当中的列表切片是一样的。

X2 = iris.data[:, :2]    # :2 表示取前两个特征，即萼片长和萼片宽

别的代码和上面完全一样，为了和上面进行区分，把 svm 和 X 的角标改了一下：

X2 = iris.data[:, :2]    # :2 表示取前两个特征，即萼片长和萼片宽
svm3 = svm.SVC(kernel="rbf", C=3, gamma="auto")
X2_train, X2_test, y2_train, y2_test = train_test_split(X2, y, test_size=0.3, random_state=218)
svm3.fit(X2_train, y2_train)
y2_predict = svm3.predict(X2_test)
print("准确率：", accuracy_score(y2_test, y2_predict))
draw1(svm3, X2)    # 绘图

你可能发现了，这段代码里定义了一个用于绘图的 draw 函数，这个函数蛮关键的，我们拆解着来写。

first，明确需求，我们希望通过前两个特征（萼片长宽）进行分类，并将结果可视化，也就是要画出决策超平面，直观地看出萼片长宽在哪一部分的花会被分到哪一类。

先把最终结果放在这，这样后面拆解每一步就会变得好理解~

下图中，背景色块相交的地方就是决策超平面（其实就是一条线），不同的色块代表花萼长宽在不同范围的鸢尾花会被分到不同的类（一个色块就是一类）。

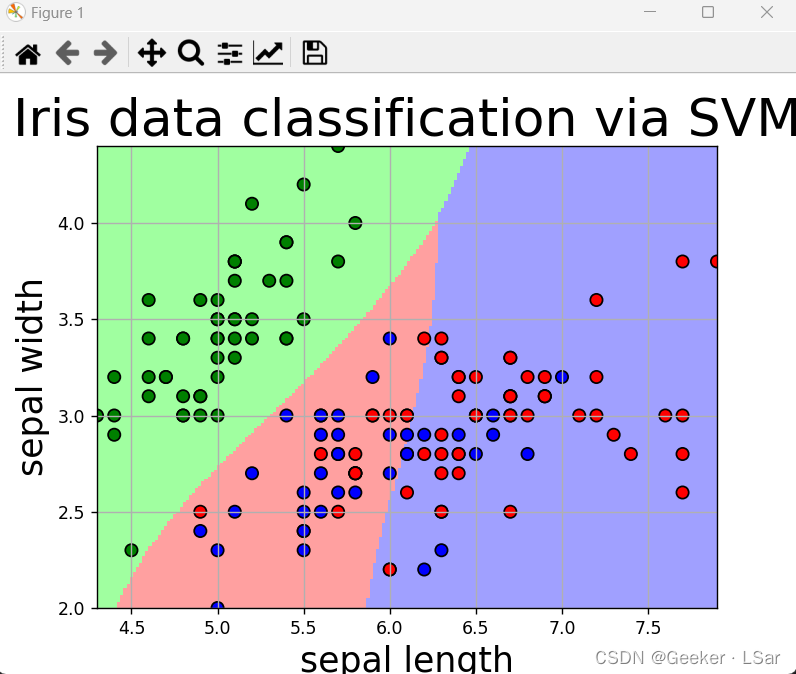
其实这块主要是数据处理 and 可视化，并且这种可视化套路其实是通用的，后面的文章中会讲 KNN（K 最近邻）算法，它的实例也可以用这一套可视化流程。

首先，花萼长宽的分布都在一定范围内，我们可以用它们的最小值和最大值作为 xy 轴的起止点，如下。

# 获取坐标值的范围
x1_min, x1_max = X[:, 0].min(), X[:, 0].max()
x2_min, x2_max = X[:, 1].min(), X[:, 1].max()
# 坐标轴范围
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)

接着，问题来了，怎么找到决策线？上图中那些表示分类的背景色块是怎么画出来的？

这个思路很好：色块其实就是一个个点密集分布组成的，我们可以在坐标系中取很多很多点（为了保证精确度，这些点之间的间隔应该相等且足够小），用已经训练好的模型预测这些点会被分到哪一类。对于分到不同类的点，用不同的颜色在坐标系中画出它们。这样这些密集的点就会形成一个“色块”，不同颜色的色块也就代表了不同的类。
（对之所以高亮这一部分就是我觉得这个思路真的太棒了！）

来写写。

first，我们要取一堆间隔足够小的点，比如在横纵坐标最小值和最大值之间都均等取 200 个值，这样一共就选取了 200*200 = 40000 个点，这么多点足以让坐标系看起来被填满了。

# 生成坐标系中的网格点（2D）
# 200j，复数，即在这个范围中取 200 个点
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]

second，目前的 x1、x2 都还只是单独的横坐标和单独的纵坐标，用 stack() 函数把它们重新组合一下，新的数组是 40000 个点的坐标。

# 构造测试点（坐标点）并输出其坐标
# stack() 方法，将两个二维数组合并成一个新的二维数组
grid_test = np.stack((x1.flat, x2.flat), axis=1)
print('坐标点的坐标数据：\n', grid_test)

输出是这样的，可以看到和图中的坐标范围是一致的。

坐标点的坐标数据:
 [[1.        0.1      ]
 [1.        0.1120603]
 [1.        0.1241206]
 ...
 [6.9       2.4758794]
 [6.9       2.4879397]
 [6.9       2.5      ]]

上一篇中提到了函数间隔，它反映点到决策超平面的距离，函数间隔大于等于 1 说明分类正确，越大说明越可能是这一类。

这里获得输出构造的坐标点的函数间隔（可以看出它们应该分到哪一类），用 decision_function() 函数，然后输出坐标点预测结果。

and then 输出一下原始数据集中的数据被分到每一类的概率，用 predict_proba() 函数。

其实这些可以不用输出，但是为了更详细地知道每个函数都干了什么，我把输出结果放在代码后面了。

# decision_function 多分类情况
# 输出样本到决策超平面的距离（函数间隔），反映属于每个分类的可能性
# 第 n 个数是属于第 n 类的可能性
# 数越大，说明越有可能属于这个分类
z = svm.decision_function(grid_test)
print('坐标点到超平面的距离（函数间隔）：\n', z)
# 预测并输出分类结果，得到 [0, 0, ..., 2, 2]
grid_hat = svm.predict(grid_test)
print('坐标点预测结果：\n', grid_hat)
# 预测并输出测试集中的数据属于每个类别的概率
probably = svm.predict_proba(X)
print('测试数据的预测概率：\n', probably)

输出结果：

坐标点到超平面的距离（函数间隔）：
 [[ 2.21808359 -0.18477028  0.86886414]
 [ 2.21824232 -0.18491925  0.86865134]
 [ 2.21838742 -0.18505706  0.86845955]
 ...
 [-0.18169166  0.85623648  2.22058861]
 [-0.18145152  0.85663691  2.22031407]
 [-0.18120477  0.85704722  2.22003204]]
 坐标点预测结果：
 [0 0 0 ... 2 2 2]
测试数据的预测概率：
 [[0.95790549 0.0183466  0.02374791]
 [0.95790549 0.0183466  0.02374791]
 [0.95498744 0.01979717 0.02521539]
 [0.95897025 0.01779033 0.02323941]（这里省略了后面的）

重要的逻辑都说完了，剩下就是画图的事情了，画图部分的代码的功能注释里都写了~

# 使得 grid_hat 和 x1 的数组形式一致
grid_hat = grid_hat.reshape(x1.shape)
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])
# pcolormesh 绘制背景颜色块（前面取坐标点并获得它们的分类结果就是为了这个）
# 用于区分坐标系中的哪一部分会被分到哪一类
# cmap 自定义颜色（用亮色绘制背景，用暗色绘制测试集中的数据点）
# 绘制测试集中的点
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)
plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark)
plt.scatter(X_test[:, 0], X_test[:, 1], s=120, facecolor='none', zorder=10)
# 坐标轴标签
plt.xlabel(iris_feature[0], fontsize=20)
plt.ylabel(iris_feature[1], fontsize=20)
# 坐标轴范围
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
# 坐标轴标题
plt.title('Iris classification based on SVM', fontsize=30)
# 绘图
plt.grid()
plt.show()

ok！画图函数已经完成，完整代码：

# 定义绘图函数（以前两个特征作为分类依据）
def draw1(svm, X):
    iris_feature = 'sepal length', 'sepal width', 'petal length', 'petal width'    # 四个特征
    # 获取坐标值的范围
    x1_min, x1_max = X[:, 0].min(), X[:, 0].max()
    x2_min, x2_max = X[:, 1].min(), X[:, 1].max()
    # 生成坐标系中的网格点（2D）
    # 200j，复数，即在这个范围中取 200 个点
    x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]
    # 构造测试点（坐标点）
    # stack() 方法，将两个二维数组合并成一个新的二维数组，并且数组 1 中的第 i 项和数组 2 中的第 i 项合并为新数组的第 i 项
    # 输出构造的点的坐标
    grid_test = np.stack((x1.flat, x2.flat), axis=1)
    print('坐标点的坐标数据：\n', grid_test)
    # decision_function 多分类情况
    # 输出样本到决策超平面的距离（函数间隔），反映属于每个分类的可能性
    # 第 n 个数是属于第 n 类的可能性
    # 数越大，说明越有可能属于这个分类
    z = svm.decision_function(grid_test)
    print('坐标点到超平面的距离（函数间隔）：\n', z)
    # 预测并输出分类结果，得到 [0, 0, ..., 2, 2]
    grid_hat = svm.predict(grid_test)
    print('坐标点预测结果：\n', grid_hat)
    # 预测并输出测试集中的数据属于每个类别的概率
    probably = svm.predict_proba(X)
    print('测试数据的预测概率：\n', probably)
    # 使得 grid_hat 和 x1 的数组形式一致
    grid_hat = grid_hat.reshape(x1.shape)
    cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
    cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])
    # pcolormesh 绘制背景颜色块（前面取坐标点并获得它们的分类结果就是为了这个）
    # 用于区分坐标系中的哪一部分会被分到哪一类
    # cmap 自定义颜色（用亮色绘制背景，用暗色绘制测试集中的数据点）
    # 绘制测试集中的点
    plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)
    plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark)
    plt.scatter(X_test[:, 0], X_test[:, 1], s=120, facecolor='none', zorder=10)
    # 坐标轴标签
    plt.xlabel(iris_feature[0], fontsize=20)
    plt.ylabel(iris_feature[1], fontsize=20)
    # 坐标轴范围
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    # 坐标轴标题
    plt.title('Iris classification based on SVM', fontsize=30)
    # 绘图
    plt.grid()
    plt.show()

最后得到的准确率是 73% 左右，和我们从图中直观看出来的是差不多的，即只按照花萼长宽进行分类的结果并不很好。

按照花瓣长宽分类和按照花萼长宽分类完全是一个道理，最后画出的图长这样，准确率在 97% 左右，说明对于鸢尾花，花瓣的特征更加鲜明，作为分类依据会更好。

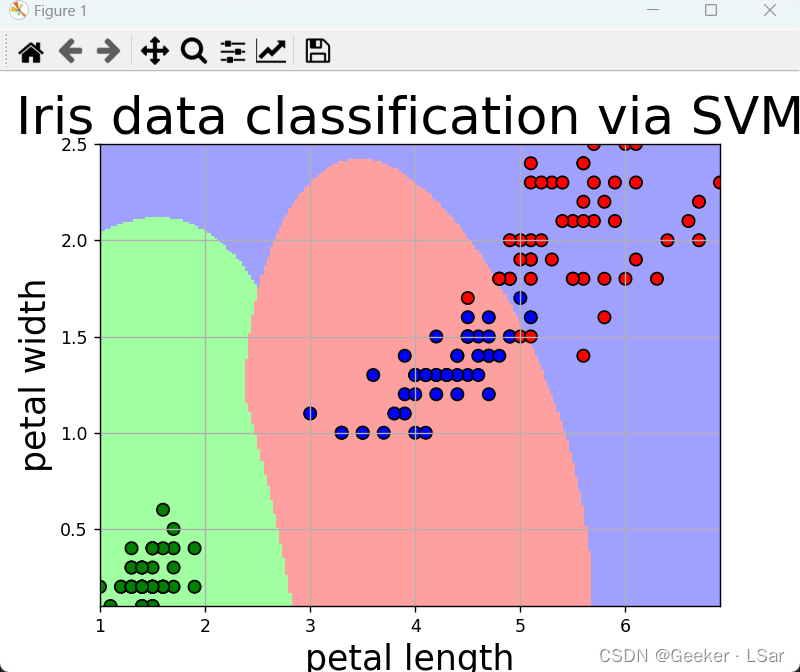
还有一个有趣的结果——按照四个特征分类的准确率居然比只按照花瓣长宽两个特征分类的准确率低（至少在本文的 “实验条件” 下是这样的），可能是因为花萼长宽中的部分数据特征不够鲜明或者有噪声数据（比如某朵花变异了之类的）。

这也说明在训练模型的时候，特征的选取有时并不是越多越好，选取特征的时候需要考虑特征是否鲜明、区分度高。如果特征选取不当，可能会对模型的性能造成负面影响。

ok！以上就是本文的全部内容啦！完整代码：

# 利用支持向量机（SVM）对鸢尾花进行分类，一共分成三类
# Scikit learn 是机器学习中常见的第三方模块，封装了常用算法，包括回归、降维、分类、聚类等
# 鸢尾花数据集：共 150 组数据，每组数据 4 个特征（四维向量）
# matplotlib 用于数据可视化
# numpy 用于科学计算

'''第一步，导入各种需要的库'''
import matplotlib.pyplot as plt    # 用于数据可视化
import matplotlib as mpl
from sklearn import svm    # 引入封装好的 SVM 算法
from sklearn.datasets import load_iris    # 引入鸢尾花数据集，共 150 组数据
from sklearn.model_selection import train_test_split    # 分割训练集和测试集的函数方法
from sklearn.metrics import accuracy_score    # 评判测试准确度的函数方法
import numpy as np    # 进行科学计算

'''第二步，输出数据集的各种信息并绘制散点图（直观分类）'''
iris = load_iris()    # 加载数据集
print(iris.target)    # 数据标签（分类结果标签）
print(iris.target_names)    # 三种鸢尾花的名字
print(iris.feature_names)    # 四个分类特征的名字
X = iris.data    # 输入数据（150 个四维向量），样本特征，[n_samples * n_features] 的二维数组
print(X.shape, X)    # X.shape，输出 X 数组的行数和列数
y = iris.target    # 数据标签 or 分类结果（共三种每种 50 个数据）
print(y.shape, y)
# 以前两个特征（花萼长度、花萼宽度）绘图
X = iris.data[:, :2]    # 切片操作，选取前两个特征
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "red", marker = "o")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "green", marker = "+")
plt.scatter(X[y == 2, 0], X[y == 2, 1], color = "blue", marker = "x")
plt.xlabel('sepal length', fontsize=20)
plt.ylabel('sepal width', fontsize=20)
plt.title('Iris names', fontsize=30)
plt.show()
# 以后两个特征（花瓣长度、花瓣宽度）绘图（发现后两个特征能够更好地区分三类鸢尾花）
X = iris.data[:, 2:]
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "red", marker = "o")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "green", marker = "+")
plt.scatter(X[y == 2, 0], X[y == 2, 1], color = "blue", marker = "x")
plt.xlabel('petal length', fontsize=20)
plt.ylabel('petal width', fontsize=20)
plt.title('Iris names', fontsize=30)
plt.show()

'''第三步，尝试用不同的方式进行训练'''
# 步骤：
# 1. 获取所需数据集（全部特征 or 某个或某几个特征（切片））
# 2. 定义支持向量机（svm.SVC()）
# 3. 划分训练集和测试集（train_test_split()）
# 4. 利用训练集进行训练（fit()）
# 5. 测试，预测测试集的输出结果（predict()）
# 6. 计算测试准确率并输出（accuracy_score()）

# svm.SVC() 函数是实现 SVM 算法的封装方法之一
# kernel：核函数类型，linear 代表线性，poly 代表多项式，rbf 代表径向基
# C：惩罚系数
# gamma：核函数中的核系数，默认为 1/n_features（特征数的倒数）

'''第一类：不分训练集和测试集，用全部特征进行分类'''
X = iris.data
svm1 = svm.SVC(kernel="rbf", C=1, gamma="auto", probability=True)
svm1.fit(X, y)    # 用全部特征进行训练
print("训练得分：", svm1.score(X, y))
print("预测：", svm1.predict([[7, 5, 2, 0.5], [7.5, 4, 7, 2]]))
print('\n')

'''第二类：分训练集和测试集，训练集训练完后用测试集测试，用全部特征进行分类'''
# test_size 表示训练数据在数据集中的占比，0.2 表示 20%
# random_state 表示随机数种子，改变该值可获得不同的分割方法
svm2 = svm.SVC(kernel="rbf", C=3, gamma="auto", probability=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=218)
svm2.fit(X_train, y_train)    # 用训练集进行训练
y_predict = svm2.predict(X_test)    # 用测试集进行测试
print("准确率：", accuracy_score(y_test, y_predict))    # 计算准确率（正确的所占百分比）
print('\n')

'''第三类：分训练集和测试集，用不同特征进行分类'''
# 定义绘图函数（以前两个特征作为分类依据）
def draw1(svm, X):
    iris_feature = 'sepal length', 'sepal width', 'petal length', 'petal width'    # 四个特征
    # 获取坐标值的范围
    x1_min, x1_max = X[:, 0].min(), X[:, 0].max()
    x2_min, x2_max = X[:, 1].min(), X[:, 1].max()
    # 生成坐标系中的网格点（2D）
    # 200j，复数，即在这个范围中取 200 个点
    x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]
    # 构造测试点（坐标点）
    # stack() 方法，将两个二维数组合并成一个新的二维数组，并且数组 1 中的第 i 项和数组 2 中的第 i 项合并为新数组的第 i 项
    # 输出构造的点的坐标
    grid_test = np.stack((x1.flat, x2.flat), axis=1)
    print('坐标点的坐标数据：\n', grid_test)
    # decision_function 多分类情况
    # 输出样本到决策超平面的距离（函数间隔），反映属于每个分类的可能性
    # 第 n 个数是属于第 n 类的可能性
    # 数越大，说明越有可能属于这个分类
    z = svm.decision_function(grid_test)
    print('坐标点到超平面的距离（函数间隔）：\n', z)
    # 预测并输出分类结果，得到 [0, 0, ..., 2, 2]
    grid_hat = svm.predict(grid_test)
    print('坐标点预测结果：\n', grid_hat)
    # 预测并输出测试集中的数据属于每个类别的概率
    probably = svm.predict_proba(X)
    print('测试数据的预测概率：\n', probably)
    # 使得 grid_hat 和 x1 的数组形式一致
    grid_hat = grid_hat.reshape(x1.shape)
    cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
    cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])
    # pcolormesh 绘制背景颜色块（前面取坐标点并获得它们的分类结果就是为了这个）
    # 用于区分坐标系中的哪一部分会被分到哪一类
    # cmap 自定义颜色（用亮色绘制背景，用暗色绘制测试集中的数据点）
    # 绘制测试集中的点
    plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)
    plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark)
    plt.scatter(X_test[:, 0], X_test[:, 1], s=120, facecolor='none', zorder=10)
    # 坐标轴标签
    plt.xlabel(iris_feature[0], fontsize=20)
    plt.ylabel(iris_feature[1], fontsize=20)
    # 坐标轴范围
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    # 坐标轴标题
    plt.title('Iris classification based on SVM', fontsize=30)
    # 绘图
    plt.grid()
    plt.show()

# 用前两个特征进行分类
X2 = iris.data[:, :2]    # :2 表示取前两个特征，即萼片长和萼片宽
svm3 = svm.SVC(kernel="rbf", C=3, gamma="auto", probability=True)
X2_train, X2_test, y2_train, y2_test = train_test_split(X2, y, test_size=0.3, random_state=218)
svm3.fit(X2_train, y2_train)
y2_predict = svm3.predict(X2_test)
print("准确率：", accuracy_score(y2_test, y2_predict))
draw1(svm3, X2)    # 绘图

print('\n')
# 定义绘图函数（以后两个特征作为分类依据）
def draw2(svm, X):
    iris_feature = 'sepal length', 'sepal width', 'petal length', 'petal width'    # 四个特征
    # 获取坐标值的范围
    x1_min, x1_max = X[:, 0].min(), X[:, 0].max()
    x2_min, x2_max = X[:, 1].min(), X[:, 1].max()
    # 生成坐标系中的网格点（2D）
    # 200j，复数，即在这个范围中取 200 个点
    x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]
    # 构造测试点（坐标点）
    # stack() 方法，将两个二维数组合并成一个新的二维数组，并且数组 1 中的第 i 项和数组 2 中的第 i 项合并为新数组的第 i 项
    # 输出构造的点的坐标
    grid_test = np.stack((x1.flat, x2.flat), axis=1)
    print('坐标点的坐标数据:\n', grid_test)
    z = svm.decision_function(grid_test)
    print('坐标点到超平面的距离（函数间隔）：\n', z)
    # 预测并输出分类结果，得到 [0, 0, ..., 2, 2]
    grid_hat = svm.predict(grid_test)
    print('坐标点预测结果：\n', grid_hat)
    # 预测并输出测试集中的数据属于每个类别的概率
    probably = svm.predict_proba(X)
    print('测试数据的预测概率：\n', probably)
    # 使得 grid_hat 和 x1 的数组形式一致
    grid_hat = grid_hat.reshape(x1.shape)
    cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
    cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])
    # pcolormesh 绘制背景颜色块（前面取坐标点并获得它们的分类结果就是为了这个）
    # 用于区分坐标系中的哪一部分会被分到哪一类
    # cmap 自定义颜色（用亮色绘制背景，用暗色绘制测试集中的数据点）
    # 绘制测试集中的点
    plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)
    plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark)
    plt.scatter(X_test[:, 0], X_test[:, 1], s=120, facecolor='none', zorder=10)
    # 坐标轴标签
    plt.xlabel(iris_feature[2], fontsize=20)
    plt.ylabel(iris_feature[3], fontsize=20)
    # 坐标轴范围
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    # 坐标轴标题
    plt.title('Iris classification based on SVM', fontsize=30)
    # 绘图
    plt.grid()
    plt.show()

# 用后两个特征进行分类
X3 = iris.data[:, 2:]    # 分割出后两个特征
svm4 = svm.SVC(kernel="rbf", C=3, gamma="auto", probability=True)
X3_train, X3_test, y3_train, y3_test = train_test_split(X3, y, test_size=0.3, random_state=218)
svm4.fit(X3_train, y3_train)    # 进行拟合（训练）
y3_predict = svm4.predict(X3_test)    # 预测（测试）
print("准确率：", accuracy_score(y3_test, y3_predict))    # 输出测试准确率
draw2(svm4, X3)

---

ok！！！！！以上就是支持向量机算法的实例！！

嘿嘿真的非常开心你能够看到这里！！一起加油！

如果有任何 bug 欢迎评论区拷打我！！

本文中所有的代码我都做了认真的分析（and 注释），希望对你有所帮助！我们下篇再见！⭐
——Geeker_LStar