目录
线性回归代码
线性回归理论
SGD算法
手撕线性回归算法
模型初始化
定义模型主体部分
定义线性回归模型训练过程
数据demo准备
模型训练与权重参数
定义线性回归预测函数
定义R2系数计算
可视化展示
预测结果
训练过程
sklearn进行机器学习
线性回归代码
class My_Model(nn.Module):
def __init__(self, input_dim):
super(My_Model, self).__init__()
# 矩阵的维度(dimensions)
self.layers = nn.Sequential(
nn.Linear(input_dim, 16),
nn.ReLU(),
nn.Linear(16, 8),
nn.ReLU(),
nn.Linear(8, 1)
)
def forward(self, x):
x = self.layers(x)
x = x.squeeze(1) # (B, 1) -> (B)
return x线性回归理论
回归算法是相对分类算法而言的,与我们想要预测的目标变量y的值类型有关。
如果目标变量y是分类型变量,如预测用户的性别(男、女),预测月季花的颜色(红、白、黄……),那我们就需要用分类算法去拟合训练数据并做出预测;
如果y是连续型变量,如预测用户的收入(4千,2万,10万……),预测患肺癌的概率(1%,50%,99%……),我们则需要用回归模型。
有时分类问题也可以转化为回归问题。可以用回归模型先预测出患肺癌的概率,然后再给定一个阈值,例如50%,概率值在50%以下为A类,50%以上为B类。
一元线性回归公式:

具象化含义:

SGD算法

手撕线性回归算法
模型初始化
### 初始化模型参数
def initialize_params(dims):
'''
输入:
dims:训练数据变量维度
输出:
w:初始化权重参数值
b:初始化偏差参数值
'''
# 初始化权重参数为零矩阵
w = np.zeros((dims, 1))
# 初始化偏差参数为零
b = 0
return w, b
w,b=initialize_params(3)#用于测试
print("w初始化是",w)
print("b初始化是",b)运行结果:
定义模型主体部分
包括线性回归公式、均方损失和参数偏导三部分
def linear_loss(X, y, w, b):
'''
输入:
X:输入变量矩阵
y:输出标签向量
w:变量参数权重矩阵
b:偏差项
输出:
y_hat:线性模型预测输出
loss:均方损失值
dw:权重参数一阶偏导
db:偏差项一阶偏导
'''
# 训练样本数量
num_train = X.shape[0]
# 训练特征数量
num_feature = X.shape[1]
# 线性回归预测输出
y_hat = np.dot(X, w) + b
# 计算预测输出与实际标签之间的均方损失
loss = np.sum((y_hat-y)**2)/num_train
# 基于均方损失对权重参数的一阶偏导数
dw = np.dot(X.T, (y_hat-y)) /num_train
# 基于均方损失对偏差项的一阶偏导数
db = np.sum((y_hat-y)) /num_train
return y_hat, loss, dw, db定义线性回归模型训练过程
### 定义线性回归模型训练过程
def linear_train(X, y, learning_rate=0.01, epochs=10000):
'''
输入:
X:输入变量矩阵
y:输出标签向量
learning_rate:学习率
epochs:训练迭代次数
输出:
loss_his:每次迭代的均方损失
params:优化后的参数字典
grads:优化后的参数梯度字典
'''
# 记录训练损失的空列表
loss_his = []
# 初始化模型参数
w, b = initialize_params(X.shape[1])
# 迭代训练
for i in range(1, epochs):
# 计算当前迭代的预测值、损失和梯度
y_hat, loss, dw, db = linear_loss(X, y, w, b)
#y_hat是预测值,loss是损失,dw是权重参数一阶偏导,db是偏差项一阶偏导
# 基于梯度下降的参数更新
w += -learning_rate * dw
b += -learning_rate * db
# 记录当前迭代的损失
loss_his.append(loss)
# 每1000次迭代打印当前损失信息
if i % 10000 == 0:
print('epoch %d loss %f' % (i, loss))
# 将当前迭代步优化后的参数保存到字典
params = {
'w': w,
'b': b
}
# 将当前迭代步的梯度保存到字典
grads = {
'dw': dw,
'db': db
}
return loss_his, params, grads其中的shape操作说明:
import numpy as np
# 创建一个示例的训练数据集 X
X = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12],
[13, 14, 15]])
# 计算训练样本数量
shape0 = X.shape[0]
shape1 = X.shape[1]
print("shape0是",shape0)
print("shape1是",shape1)运行结果:
数据demo准备
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
data = diabetes.data
target = diabetes.target
print(data.shape)
print(target.shape)
print(data[:5])
print(target[:5])
###########################################
# 导入sklearn diabetes数据接口
from sklearn.datasets import load_diabetes
# 导入sklearn打乱数据函数
from sklearn.utils import shuffle
# 获取diabetes数据集
diabetes = load_diabetes()
# 获取输入和标签
data, target = diabetes.data, diabetes.target
# 打乱数据集
X, y = shuffle(data, target, random_state=13)
# 按照8/2划分训练集和测试集
offset = int(X.shape[0] * 0.8)
# 训练集
X_train, y_train = X[:offset], y[:offset]
# 测试集
X_test, y_test = X[offset:], y[offset:]
# 将训练集改为列向量的形式
y_train = y_train.reshape((-1,1))
# 将验证集改为列向量的形式
y_test = y_test.reshape((-1,1))
# 打印训练集和测试集维度
print("X_train's shape: ", X_train.shape)
print("X_test's shape: ", X_test.shape)
print("y_train's shape: ", y_train.shape)
print("y_test's shape: ", y_test.shape)模型训练与权重参数
# 线性回归模型训练
loss_his, params, grads = linear_train(X_train, y_train, 0.01, 200000)
# 打印训练后得到模型参数
print(params)定义线性回归预测函数
### 定义线性回归预测函数
def predict(X, params):
'''
输入:
X:测试数据集
params:模型训练参数
输出:
y_pred:模型预测结果
'''
# 获取模型参数
w = params['w']
b = params['b']
# 预测
y_pred = np.dot(X, w) + b
return y_pred
# 基于测试集的预测
y_pred = predict(X_test, params)
# 打印前五个预测值
y_pred[:5]定义R2系数计算
R2系数,也称为决定系数(Coefficient of Determination),是一种用于评估回归模型拟合优度的统计指标。它表示模型对观测数据的方差解释比例,通常用于衡量回归模型的拟合程度。
R2系数的取值范围在0到1之间,具体含义如下:
- 如果R2等于0,表示模型未能解释目标变量的任何方差,即模型无法拟合数据。
- 如果R2等于1,表示模型完美拟合了数据,能够解释目标变量的所有方差。
- 如果R2在0和1之间,表示模型能够解释一部分目标变量的方差,数值越接近1,说明模型的拟合程度越好。
计算公式如下:

其中:
- SSR(Sum of Squares of Residuals)表示模型的残差平方和,即实际观测值与模型预测值之间的差异的平方和。
- SST(Total Sum of Squares)表示总平方和,即实际观测值与观测值的均值之间的差异的平方和。
R2系数越接近1,说明模型对数据的拟合越好,而越接近0则表示模型的拟合效果较差。这个指标对于评估回归模型的性能非常有用,帮助我们了解模型解释数据方差的程度。
### 定义R2系数函数
def r2_score(y_test, y_pred):
'''
输入:
y_test:测试集标签值
y_pred:测试集预测值
输出:
r2:R2系数
'''
# 测试标签均值
y_avg = np.mean(y_test)
# 总离差平方和
ss_tot = np.sum((y_test - y_avg)**2)
# 残差平方和
ss_res = np.sum((y_test - y_pred)**2)
# R2计算
r2 = 1 - (ss_res/ss_tot)
return r2可视化展示
预测结果
import matplotlib.pyplot as plt
f = X_test.dot(params['w']) + params['b']
plt.scatter(range(X_test.shape[0]), y_test)
plt.plot(f, color = 'darkorange')
plt.xlabel('X_test')
plt.ylabel('y_test')
plt.show();运行结果:

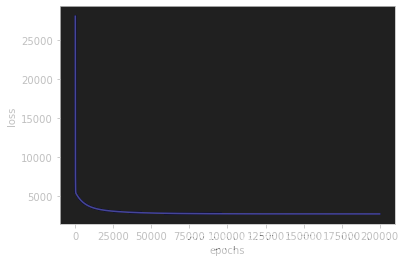
训练过程
plt.plot(loss_his, color='blue')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()运行结果:
sklearn进行机器学习
和torch.nn类似:封装好了linear函数,直接掉包
### sklearn版本为1.0.2
# 导入线性回归模块
from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score
# 创建模型实例
regr = linear_model.LinearRegression()
# 模型拟合
regr.fit(X_train, y_train)
# 模型预测
y_pred = regr.predict(X_test)
# 打印模型均方误差
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
# 打印R2
print('R2 score: %.2f' % r2_score(y_test, y_pred))