文章目录
- 算法介绍
- 实验分析
算法介绍
主成分分析(Principal Component Analysis,PCA)是一种常用的降维技术,用于在高维数据中发现最重要的特征或主成分。PCA的目标是通过线性变换将原始数据转换成一组新的特征,这些新特征被称为主成分,它们是原始特征的线性组合。
对于一个正交属性空间(各个属性之间是线性无关的)中的样本点,存在以下两个性质的超平面可对所有样本点进行恰当的表达:
- 最近重构性:样本点到这个超平面的距离足够的近。
- 最大可分性:样本点在这个超平面上的投影尽可能分开。
我们先从最近重构性的角度来进行推导:
- 假定数据样本已进行中心化,即 ∑ i x i = 0 \sum_{i}x_i=0 ∑ixi=0;
- 假定投影变换后得到的新坐标系为
{
w
1
,
2
2
,
.
.
.
,
w
d
}
\{w_1,2_2,...,w_d\}
{w1,22,...,wd},其中
w
i
w_i
wi是标准正交基。
- ∣ ∣ w i ∣ ∣ 2 = 1 ||w_i||_2=1 ∣∣wi∣∣2=1
- w i T w j = 0 ( i ≠ j ) w_i^Tw_j=0(i \ne j) wiTwj=0(i=j)
若丢弃新坐标系中的部分坐标,即将维度降低到 d ′ < d d^\prime<d d′<d,则样本点 x i x_i xi在低维坐标系下的投影是 z i = ( z i 1 ; z i 2 ; . . . ; z i d ′ ) z_i=(z_{i1};z_{i2};...;z_{id^\prime}) zi=(zi1;zi2;...;zid′),其中 z i j = w j T x i z_{ij}=w_j^Tx_i zij=wjTxi是 x i x_i xi在低维坐标系下第 j j j维的坐标。若基于 z i z_i zi来重构 x i x_i xi,则会得到 x ^ i = ∑ j = 1 d ′ z i j w j \hat x_i=\sum_{j=1}^{d^\prime}z_{ij}w_j x^i=∑j=1d′zijwj。
考虑到整个训练集,原样本点
x
i
x_i
xi与基于投影重构的样本点
x
^
i
\hat x_i
x^i之间的距离为:
∑
i
=
1
m
∣
∣
∑
j
=
1
d
′
z
i
j
w
j
−
x
i
∣
∣
2
2
=
∑
i
=
1
m
∑
j
=
1
d
′
(
z
i
j
w
j
−
x
i
)
T
(
z
i
j
w
j
−
x
i
)
=
∑
i
=
1
m
∑
j
=
1
d
′
(
z
i
j
w
j
T
−
x
i
T
)
(
z
i
j
w
j
−
x
i
)
=
∑
i
=
1
m
(
(
∑
j
=
1
d
′
z
i
j
w
j
T
)
(
∑
j
=
1
d
′
z
i
j
w
j
)
−
2
∑
j
=
1
d
′
z
i
j
w
j
T
x
i
+
x
i
T
x
i
)
(1)
\begin{aligned} \sum_{i=1}^m||\sum_{j=1}^{d^\prime}z_{ij}w_j-x_i||_2^2&=\sum_{i=1}^m\sum_{j=1}^{d^\prime}(z_{ij}w_j-x_i)^T(z_{ij}w_j-x_i)\\ &=\sum_{i=1}^m\sum_{j=1}^{d^\prime}(z_{ij}w_j^T-x_i^T)(z_{ij}w_j-x_i)\\ &=\sum_{i=1}^m\bigg((\sum_{j=1}^{d^\prime}z_{ij}w_j^T)(\sum_{j=1}^{d^\prime}z_{ij}w_j)-2\sum_{j=1}^{d^\prime}z_{ij}w_j^Tx_i+x_i^Tx_i\bigg) \end{aligned}\tag{1}
i=1∑m∣∣j=1∑d′zijwj−xi∣∣22=i=1∑mj=1∑d′(zijwj−xi)T(zijwj−xi)=i=1∑mj=1∑d′(zijwjT−xiT)(zijwj−xi)=i=1∑m((j=1∑d′zijwjT)(j=1∑d′zijwj)−2j=1∑d′zijwjTxi+xiTxi)(1)
其中
w
w
w是标准正交基,故有
∣
∣
w
i
∣
∣
2
=
1
||w_i||_2=1
∣∣wi∣∣2=1和
w
i
T
w
j
=
0
(
i
≠
j
)
w_i^Tw_j=0(i \ne j)
wiTwj=0(i=j),且
x
i
T
x
i
x_i^Tx_i
xiTxi是一个常数,令
x
i
T
x
i
=
const
x_i^Tx_i=\text{const}
xiTxi=const,所以(1)式可以简化为:
∑
i
=
1
m
∣
∣
∑
j
=
1
d
′
z
i
j
w
j
−
x
i
∣
∣
2
2
=
∑
i
=
1
m
(
(
z
i
1
w
1
T
+
z
i
2
w
2
T
+
.
.
.
+
z
i
d
′
w
d
′
T
)
(
z
i
1
w
1
+
z
i
2
w
2
+
.
.
.
+
z
i
d
′
w
d
′
)
−
2
z
i
T
[
w
1
T
w
2
T
.
.
.
w
d
′
T
]
x
i
)
+
const
=
∑
i
=
1
m
(
∑
j
=
1
d
′
z
i
j
T
z
i
j
−
2
z
i
T
w
T
x
i
)
+
const
=
∑
i
=
1
m
(
z
i
T
z
i
−
2
z
i
T
z
i
)
+
const
=
−
∑
i
=
1
m
z
i
T
z
i
+
const
=
−
(
z
1
T
z
1
+
z
2
T
z
2
+
.
.
.
+
z
m
T
z
m
)
+
const
=
−
∑
i
=
1
m
t
r
(
z
i
T
z
i
)
+
const
(2)
\begin{aligned} \sum_{i=1}^m||\sum_{j=1}^{d^\prime}z_{ij}w_j-x_i||_2^2&=\sum_{i=1}^m\bigg((z_{i1}w_1^T+z_{i2}w_2^T+...+z_{id^\prime}w_{d^\prime}^T)(z_{i1}w_1+z_{i2}w_2+...+z_{id^\prime}w_{d^\prime})-2z_i^T\begin{bmatrix} w_1^T \\ w_2^T \\ ...\\ w_{d^\prime}^T \\ \end{bmatrix}x_i\bigg)+\text{const}\\ &=\sum_{i=1}^m\bigg(\sum_{j=1}^{d^\prime}z_{ij}^Tz_{ij}-2z_i^Tw^Tx_i\bigg)+\text{const}\\ &=\sum_{i=1}^m\bigg(z_i^Tz_i-2z_i^Tz_i\bigg)+\text{const}\\ &=-\sum_{i=1}^m z_i^Tz_i+\text{const}\\ &=-(z_1^Tz_1+z_2^Tz_2+...+z_m^Tz_m)+\text{const}\\ &=-\sum_{i=1}^mtr(z_i^Tz_i)+\text{const} \end{aligned}\tag{2}
i=1∑m∣∣j=1∑d′zijwj−xi∣∣22=i=1∑m((zi1w1T+zi2w2T+...+zid′wd′T)(zi1w1+zi2w2+...+zid′wd′)−2ziT
w1Tw2T...wd′T
xi)+const=i=1∑m(j=1∑d′zijTzij−2ziTwTxi)+const=i=1∑m(ziTzi−2ziTzi)+const=−i=1∑mziTzi+const=−(z1Tz1+z2Tz2+...+zmTzm)+const=−i=1∑mtr(ziTzi)+const(2)
又因为
t
r
(
A
B
)
=
t
r
(
B
A
)
tr(AB)=tr(BA)
tr(AB)=tr(BA)故(2)式可变为:
∑
i
=
1
m
∣
∣
∑
j
=
1
d
′
z
i
j
w
j
−
x
i
∣
∣
2
2
=
−
∑
i
=
1
m
t
r
(
z
i
z
i
T
)
+
const
=
−
t
r
(
∑
i
=
1
m
z
i
z
i
T
)
+
const
=
−
t
r
(
∑
i
=
1
m
w
T
x
i
x
i
T
w
)
+
const
=
−
t
r
(
w
T
(
∑
i
=
1
m
x
i
x
i
T
)
w
)
+
const
∝
−
t
r
(
w
T
(
∑
i
=
1
m
x
i
x
i
T
)
w
)
(3)
\begin{aligned} \sum_{i=1}^m||\sum_{j=1}^{d^\prime}z_{ij}w_j-x_i||_2^2&=-\sum_{i=1}^mtr(z_iz_i^T)+\text{const}\\ &=-tr\bigg(\sum_{i=1}^m z_iz_i^T\bigg)+\text{const}\\ &=-tr\bigg(\sum_{i=1}^mw^Tx_ix_i^Tw\bigg)+\text{const}\\ &=-tr\bigg(w^T(\sum_{i=1}^mx_ix_i^T)w\bigg)+\text{const}\\ &\propto-tr\bigg(w^T(\sum_{i=1}^mx_ix_i^T)w\bigg) \end{aligned}\tag{3}
i=1∑m∣∣j=1∑d′zijwj−xi∣∣22=−i=1∑mtr(ziziT)+const=−tr(i=1∑mziziT)+const=−tr(i=1∑mwTxixiTw)+const=−tr(wT(i=1∑mxixiT)w)+const∝−tr(wT(i=1∑mxixiT)w)(3)
根据最近重构性,式(3)应该被最小化,有:
min W − tr ( W T X X T W ) s.t. W T W = E . (4) \begin{aligned} & \min _{\mathbf{W}}-\operatorname{tr}\left(\mathbf{W}^{\mathrm{T}} \mathbf{X} \mathbf{X}^{\mathrm{T}} \mathbf{W}\right) \\ & \text { s.t. } \mathbf{W}^{\mathrm{T}} \mathbf{W}=\mathbf{E} . \end{aligned} \tag{4} Wmin−tr(WTXXTW) s.t. WTW=E.(4)
这就是PCA的最终优化目标。
接着我们从最大可分性出发,我们知道样本点 x i x_i xi在新空间中的超平面上的投影是 W T x i W^Tx_i WTxi,若所有的样本点的投影能尽可能的分开,则应该使投影后样本点的方差最大化。
在降维和投影中,我们通常不使用传统的方差定义,因为这里我们不涉及到随机变量和随机过程。相反,我们使用方差的术语来描述投影后样本点在新空间中的变异性,这更多地是一种几何上的直觉而非统计学中方差的定义。
方差的形式为 x i T W W T x i x_i^T W W^T x_i xiTWWTxi,可以从以下几何角度解释:
-
投影方向: 投影矩阵 W W W 确定了投影的方向,每一列表示新空间的基向量。
-
样本点变异性: x i x_i xi 是原始空间中的样本点, W T x i W^Tx_i WTxi 是投影到新空间后的样本点。 x i x_i xi 和 W T x i W^Tx_i WTxi 之间的差异,即 x i − W T x i x_i - W^Tx_i xi−WTxi,表示样本点在投影方向上的变异性。
-
方差形式: 方差的形式 x i T W W T x i x_i^T W W^T x_i xiTWWTxi 表示了在投影方向上的样本点变异性的量度。这个形式的计算实际上考虑了样本点在投影方向上的平方和,类似于方差的直觉。
-
最大化分离性: 当我们尝试最大化这个“方差”时,我们实际上是在尝试选择一个投影方向,使得在新空间中的样本点在投影方向上的变异性最大化。这有助于确保在新空间中,样本点能够尽可能地分开,提高了样本点在新空间中的可分性。
请注意,这种形式的“方差”并不是统计学中方差的定义,而更多是一种在降维和投影问题中用于描述样本点分布情况的术语。这种定义的目标是为了在新空间中找到一个有利于分离的方向,以便更好地实现降维和分类等任务。
故投影后样本点的方差是
V a r ( W T x i ) = V a r ( x i T W ) = ∑ i W T x i x i T W = W T ( ∑ i x i x i T ) W = W T ( x 1 x 1 T + x 2 x 2 T + . . . + x m x m T ) W = W T ( ∑ i t r ( x i x i T ) ) W = t r ( W T X X T W ) (5) \begin{aligned} Var(W^Tx_i)&=Var(x_i^TW)\\ &=\sum_iW^Tx_ix_i^TW\\ &=W^T(\sum_ix_ix_i^T)W\\ &=W^T\bigg( x_1x_1^T+x_2x_2^T+...+x_mx_m^T\bigg)W\\ &=W^T\bigg( \sum_itr(x_ix_i^T)\bigg)W\\ &=tr(W^TXX^TW) \end{aligned}\tag{5} Var(WTxi)=Var(xiTW)=i∑WTxixiTW=WT(i∑xixiT)W=WT(x1x1T+x2x2T+...+xmxmT)W=WT(i∑tr(xixiT))W=tr(WTXXTW)(5)
于是优化目标可写成:
max
W
tr
(
W
T
X
X
T
W
)
s.t.
W
T
W
=
E
,
(6)
\begin{aligned} \max _{\mathbf{W}} & \operatorname{tr}\left(\mathbf{W}^{\mathrm{T}} \mathbf{X} \mathbf{X}^{\mathrm{T}} \mathbf{W}\right) \\ \text { s.t. } & \mathbf{W}^{\mathrm{T}} \mathbf{W}=\mathbf{E}, \end{aligned} \tag{6}
Wmax s.t. tr(WTXXTW)WTW=E,(6)
显然式(4)和式(6)等价,故对式(4)或(6)使用拉格朗日乘子法,引入拉格朗日乘子矩阵
Λ
\Lambda
Λ,我们的目标是 :
L
(
W
,
Λ
)
=
t
r
(
W
T
X
X
T
W
)
−
t
r
(
Λ
(
W
T
W
−
E
)
)
(7)
\mathcal{L}(\mathbf{W,\Lambda)}=tr(\mathbf{W^TXX^TW)}-tr(\mathbf{\Lambda(W^TW-E))} \tag{7}
L(W,Λ)=tr(WTXXTW)−tr(Λ(WTW−E))(7)
现在我们分别对 W W W和 Λ \Lambda Λ求偏导,并令其为零有:
∂ L ∂ W = 2 X X T W − 2 Λ T W = 0 (8) \frac{\partial \mathcal{L}}{\partial \mathbf{W}}=2 \mathbf{X} \mathbf{X}^{\mathrm{T}} \mathbf{W}-2 \Lambda^{\mathrm{T}} \mathbf{W}=0 \tag{8} ∂W∂L=2XXTW−2ΛTW=0(8)
∂ L ∂ Λ = − ( W T W − E ) = 0 (9) \frac{\partial \mathcal{L}}{\partial \boldsymbol{\Lambda}}=-\left(\mathbf{W}^{\mathrm{T}} \mathbf{W}-\mathbf{E}\right)=0 \tag{9} ∂Λ∂L=−(WTW−E)=0(9)
最终得到:
X X T W = Λ T W (10) \mathbf{XX^TW}=\mathbf{\Lambda^TW} \tag{10} XXTW=ΛTW(10)
W T W = E (11) \mathbf{W^TW=E} \tag{11} WTW=E(11)
其中 Λ = d i a g ( λ 1 , λ 2 , . . . , λ d ′ ) ∈ R d ′ × d ′ \Lambda=diag(\lambda_1,\lambda_2,...,\lambda_d^\prime) \in \mathbb{R}^{d^\prime\times d^\prime} Λ=diag(λ1,λ2,...,λd′)∈Rd′×d′。
将(10)式展开有:
X X T w i = λ i w i (12) \mathbf{XX^T}w_i=\lambda_iw_i\tag{12} XXTwi=λiwi(12)
最后我们只需要对 X X T \mathbf{XX^T} XXT进行特征值分解,其中 λ i \lambda_i λi是矩阵 X X T \mathbf{XX^T} XXT的特征值, w i w_i wi是 λ i \lambda_i λi所对应的单位特征向量。
最终我们选取前 d ′ d^\prime d′个特征值所对应的特征向量构成的 W = ( w 1 , w 2 , . . . , w d ′ ) \mathbf{W}=(w_1,w_2,...,w_{d^\prime}) W=(w1,w2,...,wd′),这就是我们所求的最终解。
其PCA算法流程图如下图所示:

这就出现了一个新的问题,低维空间维数 d ′ d^\prime d′是由用户事先决定的,那么该如何确定 d ′ d^\prime d′?
我们可以从重构的角度来设置一个重构阈值,例如 t = 95 % t=95\% t=95%,然后选取使得下式成立的最小 d ′ d^\prime d′值:
∑ i = 1 d ′ λ i ∑ i = 1 d λ i ⩾ t \frac{\sum_{i=1}^{d^{\prime}} \lambda_i}{\sum_{i=1}^d \lambda_i} \geqslant t ∑i=1dλi∑i=1d′λi⩾t
对于式(8)和(9)求偏导过程如下:
∂ L ∂ W = ∂ ( t r ( W T X X T W ) − t r ( Λ ( W T W − E ) ) ) ∂ W = ∂ t r ( W T X X T W ) ∂ W − ∂ t r ( Λ ( W T W − E ) ) ∂ W (13) \begin{aligned} \frac{\partial \mathcal{L}}{\partial \mathbf{W}}&=\frac{\partial\bigg( \ tr(\mathbf{W^TXX^TW})-tr(\mathbf{\Lambda(W^TW-E))}\bigg)}{\partial \mathbf{W}}\\ &=\frac{\partial \ tr(\mathbf{W^TXX^TW})}{\partial \mathbf{W}}-\frac{\partial \ tr(\mathbf{\Lambda(W^TW-E))}}{\partial \mathbf{W}} \end{aligned} \tag{13} ∂W∂L=∂W∂( tr(WTXXTW)−tr(Λ(WTW−E)))=∂W∂ tr(WTXXTW)−∂W∂ tr(Λ(WTW−E))(13)
对式(13)我们可以用迹的性质, t r ( A B ) = t r ( B A ) tr(AB)=tr(BA) tr(AB)=tr(BA),故我们可将 W T X X T W \mathbf{W^TXX^TW} WTXXTW和 Λ ( W T W − E ) \mathbf{\Lambda(W^TW-E)} Λ(WTW−E)重新排列成 W W T X T X \mathbf{WW^TX^TX} WWTXTX和 Λ ( W W T − E ) \mathbf{\Lambda(WW^T-E)} Λ(WWT−E),即:
∂ L ∂ W = ∂ t r ( W W T X T X ) ∂ W − ∂ t r ( Λ ( W W T − E ) ) ∂ W = ∂ t r ( W W T X T X ) ∂ ( W W T ) ⋅ ∂ ( W W T ) ∂ W − 2 Λ W = X T X ⋅ 2 W − 2 Λ W = 2 X X T W − 2 Λ T W (14) \begin{aligned} \frac{\partial \mathcal{L}}{\partial \mathbf{W}}&=\frac{\partial \ tr(\mathbf{WW^TX^TX})}{\partial \mathbf{W}}-\frac{\partial \ tr(\mathbf{\Lambda(WW^T-E))}}{\partial \mathbf{W}}\\ &=\frac{\partial\ tr(\mathbf{W W^T X^T X)}}{\partial \mathbf{(W W^T)}} \cdot \frac{\partial\mathbf{(W W^T)}}{\partial \mathbf{W}}-2\mathbf{\Lambda W}\\ &=\mathbf{X^TX}\cdot 2\mathbf{W}-2\mathbf{\Lambda W}\\ &=2 \mathbf{X} \mathbf{X}^{\mathrm{T}} \mathbf{W}-2 \Lambda^{\mathrm{T}} \mathbf{W} \end{aligned}\tag{14} ∂W∂L=∂W∂ tr(WWTXTX)−∂W∂ tr(Λ(WWT−E))=∂(WWT)∂ tr(WWTXTX)⋅∂W∂(WWT)−2ΛW=XTX⋅2W−2ΛW=2XXTW−2ΛTW(14)
对于式(7)约束条件为什么可以写成迹的形式?
在这个问题中,我们要证明在优化问题中 t r ( Λ ( W T W − E ) ) tr(\mathbf{\Lambda(W^TW-E)}) tr(Λ(WTW−E))和 Λ ( W T W − E ) \mathbf{\Lambda(W^TW-E)} Λ(WTW−E)是等价的,即它们对于最优解是相同的。下面我们来给出详细的证明!
为此,我们可以比较两者的梯度。考虑对拉格朗日函数 L ( W , Λ ) \mathcal{L}(\mathbf{W,\Lambda}) L(W,Λ)是关于 W W W的偏导数。首先计算 L \mathcal{L} L对 W \mathbf{W} W的梯度得到式(10),解出最优解 W ⋆ \mathbf{W^\star} W⋆。现在我们比较两种形式对最优解的梯度。
-
对于 t r ( Λ ( W T W − E ) ) tr(\mathbf{\Lambda(W^TW-E)}) tr(Λ(WTW−E)):
∂ t r ( Λ ( W T W − E ) ) ∂ W = 2 Λ W \frac{\partial tr(\mathbf{\Lambda(W^T W-E))}}{\partial \mathbf{W}}=2 \Lambda \mathbf{W} ∂W∂tr(Λ(WTW−E))=2ΛW -
对于 Λ ( W T W − E ) \mathbf{\Lambda(W^TW-E)} Λ(WTW−E):
∂ Λ ( W T W − E ) ∂ W = 2 Λ W \frac{\partial \mathbf{\Lambda(W^T W-E)}}{\partial \mathbf{W}}=2 \Lambda \mathbf{W} ∂W∂Λ(WTW−E)=2ΛW
从上面的梯度计算中,我们可以看到,两种形式的梯度在最优解处是相同的,因此在优化问题中 t r ( Λ ( W T W − E ) ) tr(\mathbf{\Lambda(W^TW-E)}) tr(Λ(WTW−E))和 Λ ( W T W − E ) \mathbf{\Lambda(W^TW-E)} Λ(WTW−E)是等价。这意味着它们会产生相同的最优解。
我们将矩阵运算转化为迹(trace)形式在某些情况下具有优势,尤其是在涉及到矩阵的导数计算和优化问题时。以下是一些使用迹的好处:
-
简化导数计算: 迹运算的导数计算相对简单,尤其是对于迹的线性性质,这可以简化复杂矩阵函数的导数计算。这种简化对于深度学习等领域中的梯度下降等优化问题很有用。
-
矩阵的不可交换性: 在矩阵乘法中,矩阵的乘法是不可交换的,即 A B AB AB一般不等于 B A BA BA。但是,通过转化为迹形式,有时可以使计算更加简单。
-
整合约束条件: 在优化问题中,通过引入拉格朗日乘子法,迹运算可以用于整合约束条件,使得问题的形式更加一致,更容易处理。
-
向量化和矩阵形式: 将矩阵运算表示为迹形式有助于使用向量化和矩阵形式,从而更好地利用硬件加速(如GPU)来加速计算。
实验分析
数据集如下图所示:
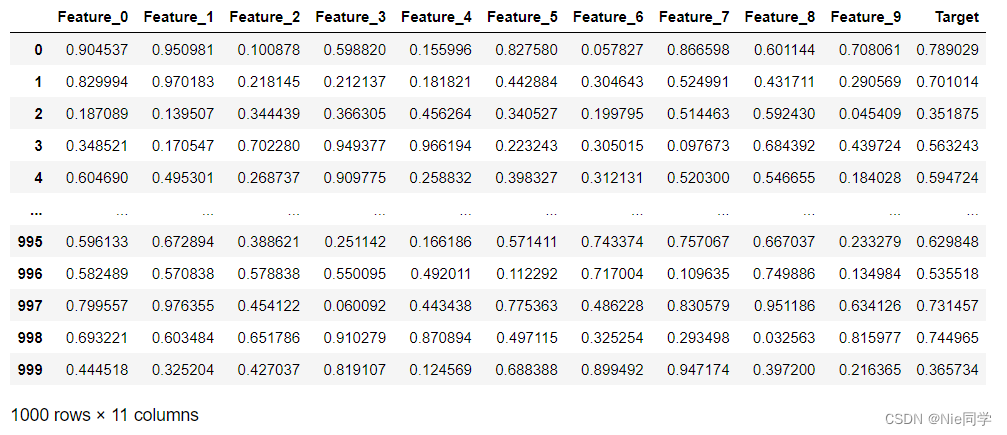
读入数据集:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 读取数据
data = pd.read_csv('data/correlated_dataset.csv')
# 提取特征列
features = data.drop('Target', axis=1)
计算协方差矩阵以及特征值分解:
# 计算协方差矩阵
cov_matrix = features.cov()
# 特征值分解
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
选择最小 d ′ d^\prime d′值:
# 选择重构阈值
reconstruction_threshold = 0.95
# 计算特征值的累积和
eigenvalue_cumsum = np.cumsum(eigenvalues) / np.sum(eigenvalues)
# 找到满足阈值条件的最小d'
selected_d_prime = np.argmax(eigenvalue_cumsum >= reconstruction_threshold) + 1
# 输出选择的最小d'
print("选择的最小降维维度 d' =", selected_d_prime)
选择的最小降维维度 d' = 7
重新计算特征值和特征向量:
# 根据选择的最小d'重新计算选取的特征值和特征向量
selected_indices_reconstructed = np.argsort(eigenvalues)[-selected_d_prime:][::-1]
selected_eigenvalues_reconstructed = eigenvalues[selected_indices_reconstructed]
selected_eigenvectors_reconstructed = eigenvectors[:, selected_indices_reconstructed]
# 投影数据到新的空间
reduced_data_reconstructed = features.dot(selected_eigenvectors_reconstructed)
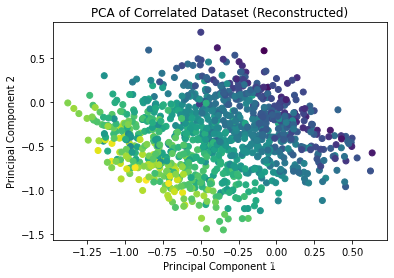
可视化数据降维后的数据:
plt.scatter(reduced_data_reconstructed.iloc[:, 0], reduced_data_reconstructed.iloc[:, 1], c=data['Target'], cmap='viridis')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA of Correlated Dataset (Reconstructed)')
plt.show()