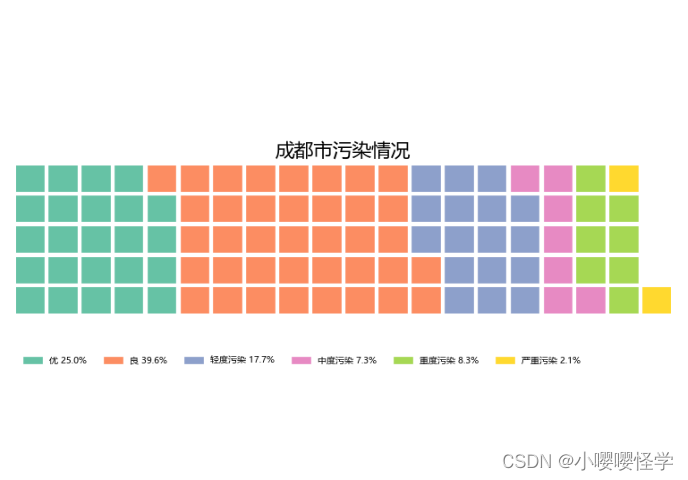
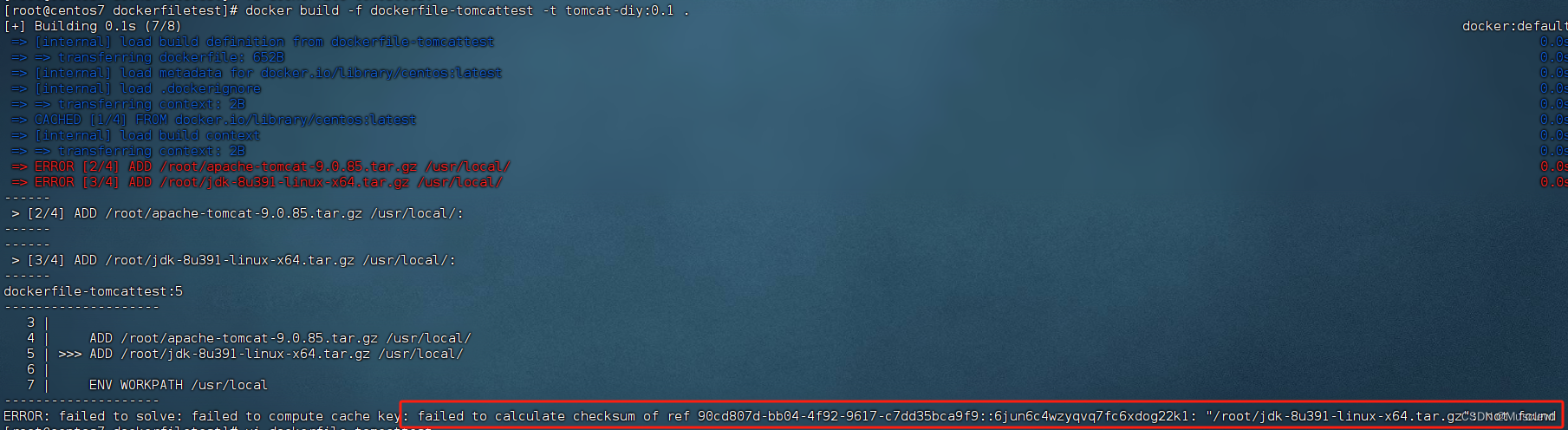
今天主要围绕并查集的一些今典题目展开：

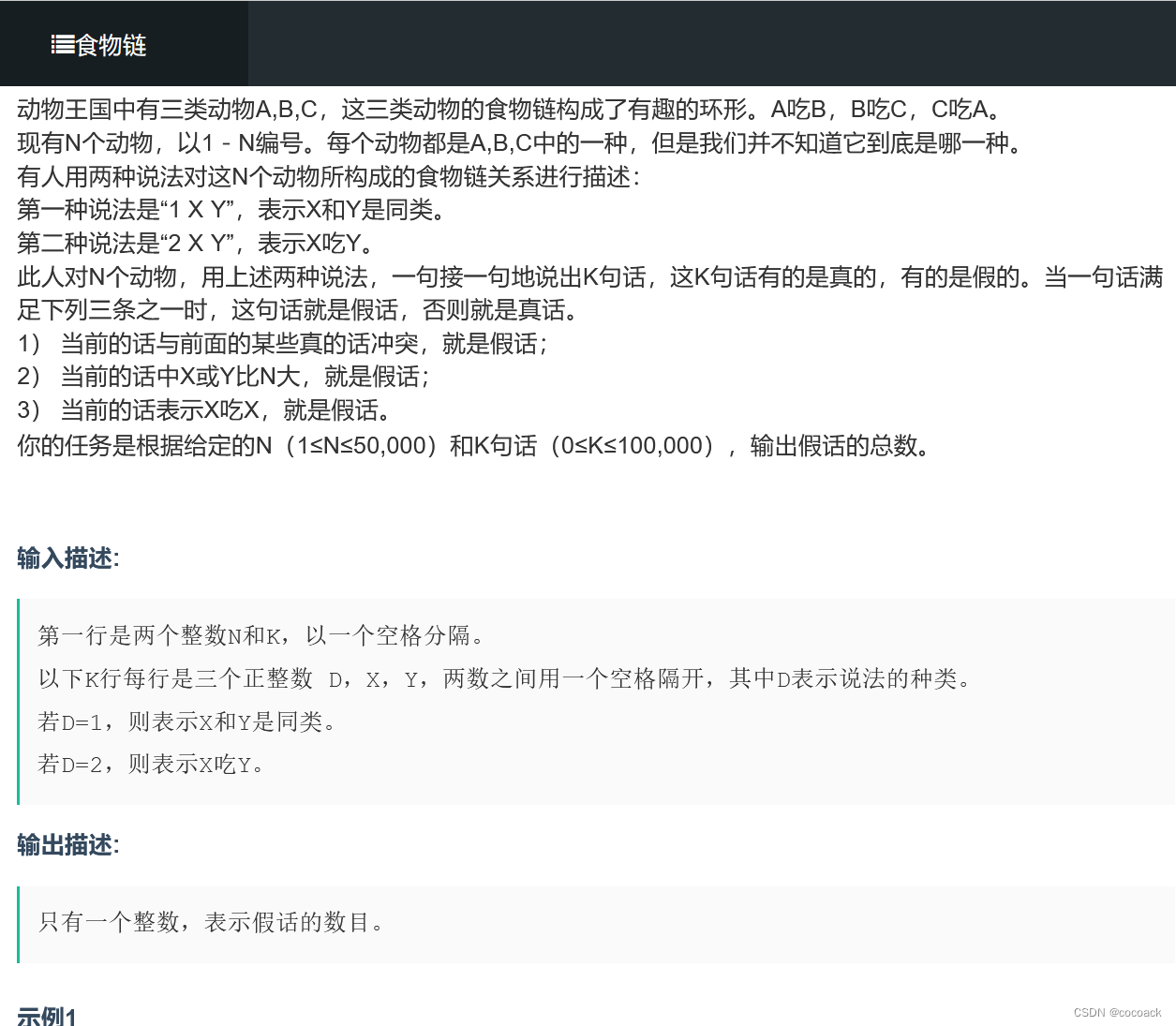
在这里，我们把逻辑真的组合，用并查集即可。一开始，我觉得把a,b,c等价，把第一个赋a,接下来推即可，但这样在判断矛盾时还需要选择合适的点find，于是我们把所有可能合并，这样find时就可以轻松一点，下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,k,fa[200000],cnt;
int find(int x){
    if(fa[x]==x) return x;
    else return fa[x]=find(fa[x]);
}
void merge(int x,int y){
    fa[find(x)]=find(y);
}
int main(){
    cin>>n>>k;
    int x,y,z;
    for(int i=1;i<=3*n;i++) fa[i]=i;
    for(int i=1;i<=k;i++){
        scanf("%d%d%d",&x,&y,&z);
        if(y>n||z>n){
            cnt++;
            continue;
        }
        if(x==1){
            if(find(y)==find(z+n)||find(y)==find(z+2*n)) cnt++;
            else{
                merge(y,z);
                merge(y+n,z+n);
                merge(y+2*n,z+2*n);
            }      
        }
        else{
             if(find(y)==find(z+2*n)||find(y)==find(z)) cnt++;
            else{
                merge(y,z+n);
                merge(y+n,z+2*n);
                merge(y+2*n,z);
            } 
        }
    }
    cout<<cnt;
}

接下来让我们看看一道有趣的“并拆集”：

首先，假如没有D，只要在根上存那集合上的最大权值，合并时维护一下即可。

那对于D ，我们只要先存D询问，事先把要删的全删，再从后往前合并即可。

接题：

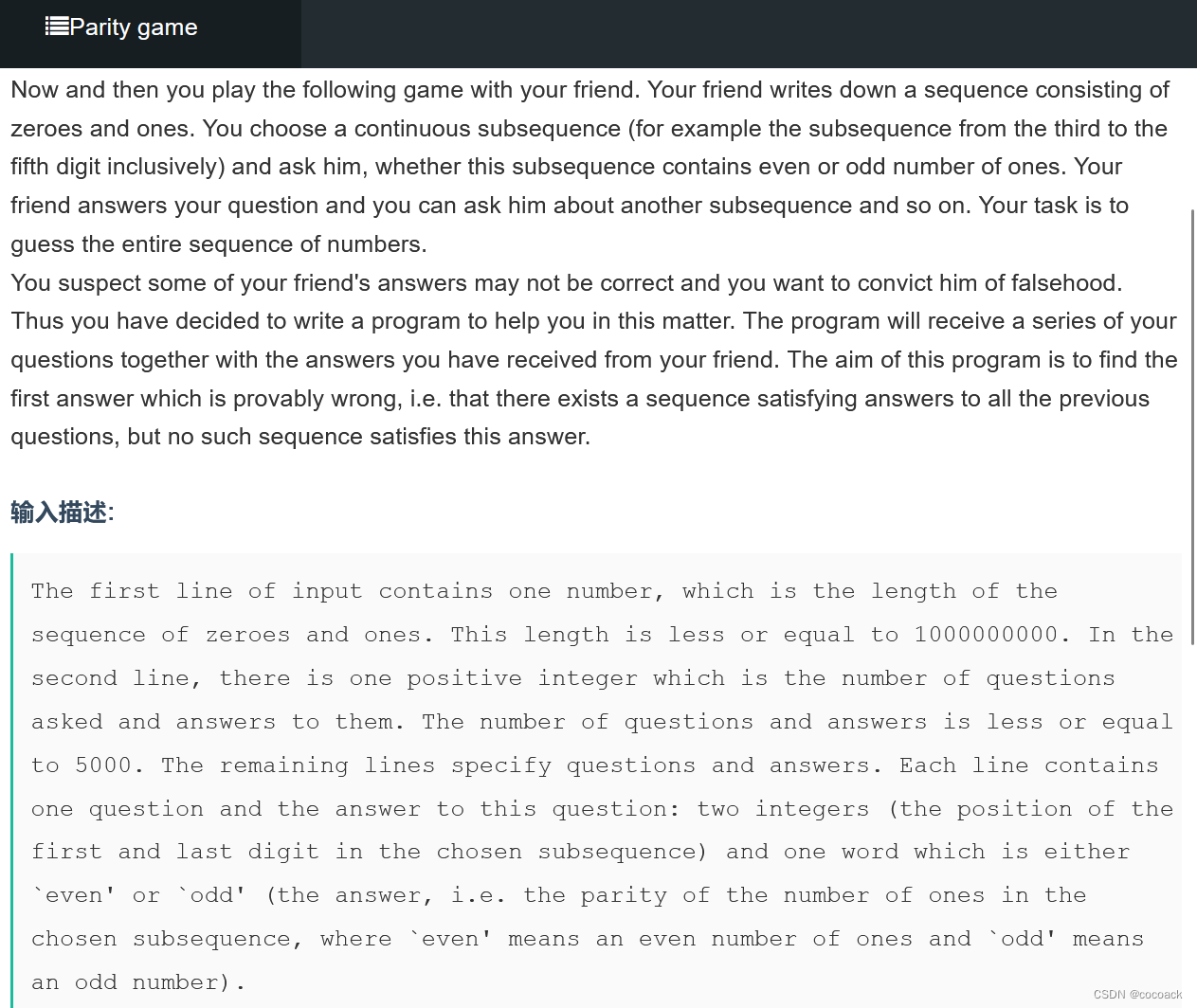
下面为分析：

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
map<int,int> mp;
int n,m;
int find(int x){
	if(mp[x]==x) return x;
	else return mp[x]=find(mp[x]);
}
void merge(int x,int y){
	mp[find(x)]=find(y);
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int x,y;
		string s;
		scanf("%d%d",&x,&y);
        if(mp.count(y)==0) mp[y]=y;
        if(mp.count(y+n+1)==0) mp[y+n+1]=y+n+1;
        if(mp.count(x-1)==0) mp[x-1]=x-1;
        if(mp.count(x+n)==0) mp[x+n]=x+n;
		cin>>s;
		if(x>n||y>n){
			cout<<i-1;
			return 0;
		}
		if(s=="even"){
			if(find(x-1)==find(y+n+1)){
				cout<<i-1;
				return 0;
			}
			else{
				merge(x-1,y);
				merge(x+n,y+n+1);
			}
		}
		else{
			if(find(x-1)==find(y)){
				cout<<i-1;
				return 0;
			}
			else{
				merge(x-1,y+n+1);
				merge(x+n,y);
			}
		}
	}
	cout<<m;
	return 0;
}

这里有几个注意的：

1.map离散化 2.注意0也要包括，因此总数为2*n+2