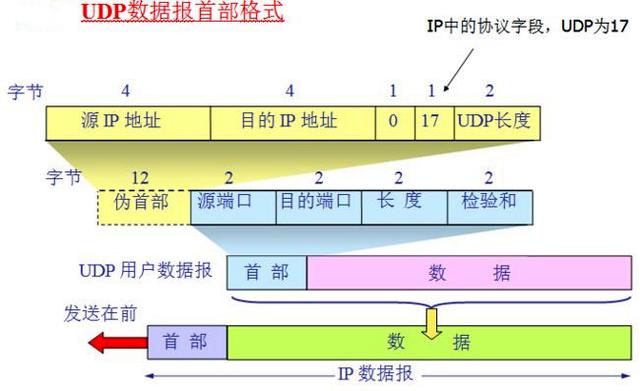
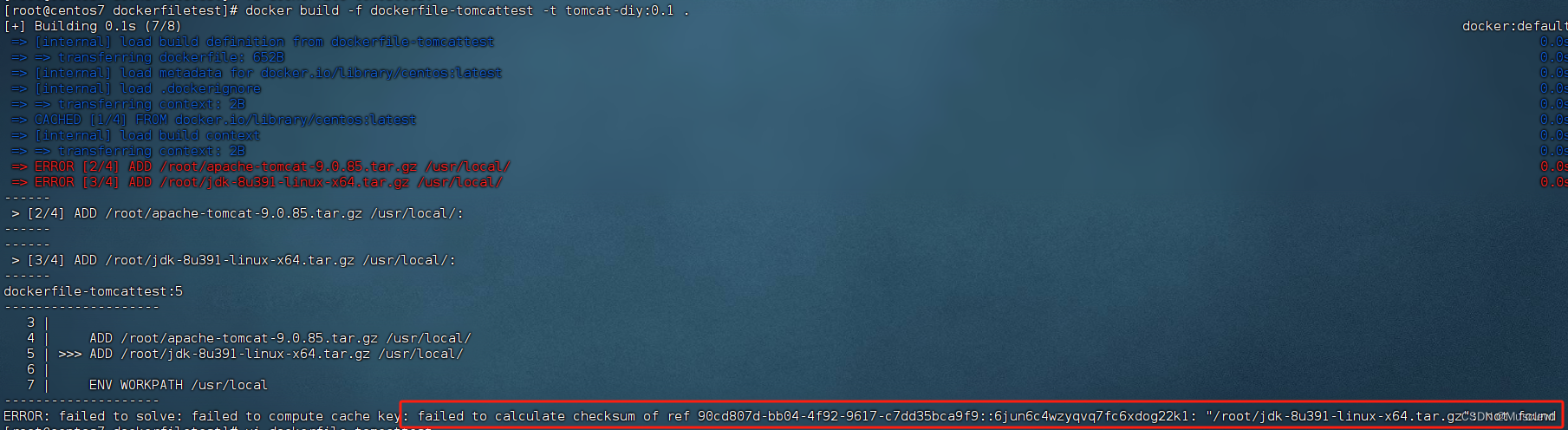
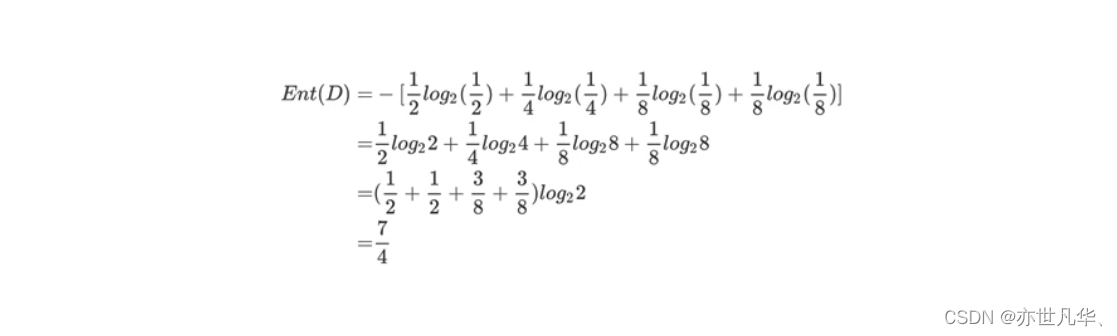决策树思想的来源非常朴素,程序设计中的条件分支结构就是if-else结构,最早的决策树就是利用这类结构分割数据的一种分类学习方法
目录
初识决策树
决策树原理
cart剪枝
特征提取
泰坦尼克号乘客生存预测(实操)
回归决策树
初识决策树
决策树是一种树形结构,其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出,最后每个叶节点代表一种分类结果,本质是一颗由多个判断节点组成的树。如何理解这段话呢?举个例子如下:
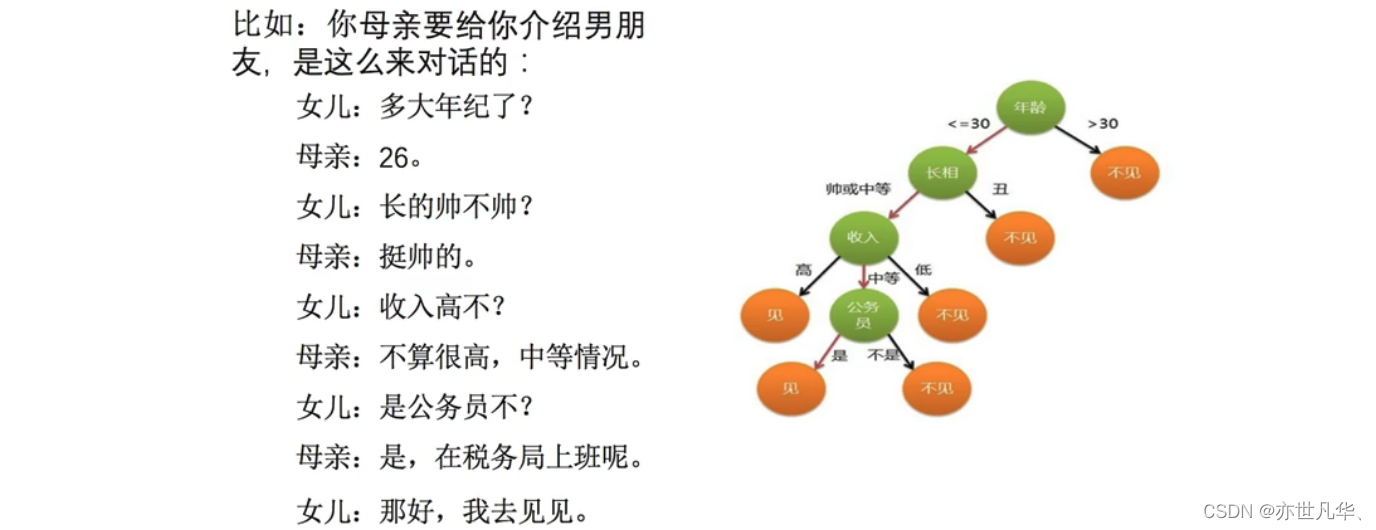
上面案例是女生通过定性的主观意识,把年龄放到最上面,那么如果需要对这一过程进行量化,该如何处理呢?此时需要用到信息论中的知识:信息熵,信息增益。
熵:物理学上,熵(Entropy)是“混乱"程度的量度。系统越有序,熵值越低;系统越混乱或者分散,熵值越高。
1948年香农提出了信息熵(Entropy)的概念:
1)从信息的完整性上进行的描述:
当系统的有序状态一致时,数据越集中的地方熵值越小,数据越分散的地方熵值越大。
2)从信息的有序性上进行的描述:
当数据量一致时,系统越有序,熵值越低;系统越混乱或者分散,熵值越高。
“信息熵”(informationentropy)是度量样本集合纯度最常用的一种指标:

根据上面的公式,我们进行如下案例的计算:
案例1:
假设我们没有看世界杯的比赛,但是想知道哪支球队会是冠军,我们只能猜测某支球队是或不是冠军,然后观众用对或不对来回答,我们想要猜测次数尽可能少,你会用什么方法?
答案:二分法:假如有16支球队,分别编号,先问是否在1-8之间,如果是就继续问是否在1-4之间,以此类推,直到最后判断出冠军球队是哪支。如果球队数量是16,我们需要问4次来得到最后的答案。那么世界冠军这条消息的信息熵就是4。
那么信息熵等于4,是如何进行计算的呢?
Ent(D)=-(p1*logp1+p2*logp2+...+p16*logp16),其中p1,·.·,p16分别是这16支球队夺冠的概率。当每支球队夺冠概率相等都是1/16的时:Ent(D)=-(16*1/16*log1/16))=4每个事件概率相同时,熵最大,这件事越不确定。
案例2:
篮球比赛里,有4个球队{A,B,C,D},获胜概率分别为{1/2,1/4,1/8,1/8}求Ent(D)
决策树原理
决策树的原理基于对特征值的分裂和判断,通过构建一个由节点和分支组成的树结构来进行决策。根据不同的问题类型和相关准则,决策树算法可以灵活地适应各种分类和回归任务。决策树算法的原理可以简述如下:
特征选择:决策树的构建从根节点开始,每次选择一个最优的特征作为当前节点的分裂条件。常用的特征选择准则有信息增益、信息增益率、基尼系数等,这些准则衡量了特征对于分类结果的重要程度。
信息增益:以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性,熵越大,样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。即:信息增益=entroy(前)-entroy(后),注意:信息增益表示得知特征X的信息而使得类Y的信息熵减少的程度。其定义与公式如下:

公式的详细解释如下:
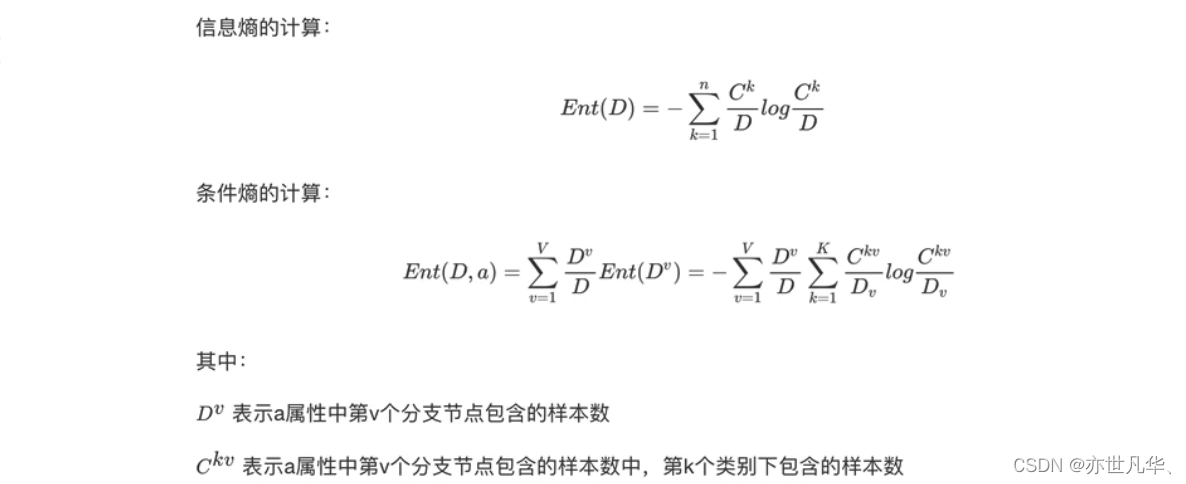
一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的"纯度提升"越大。因此,我们可用信息增益来进行决策树的划分属性选择,著名的ID3决策树学习算法[Quinlan,1986]就是以信息增益为准则来选择划分属性。其中,ID3名字中的ID是IterativeDichotomiser(迭代二分器)的简称。
通过如下案例进行说明:如下图,第一列为论坛号码,第二列为性别,第三列为活跃度,最后一列用户是否流失。我们要解决一个问题:性别和活跃度两个特征,哪个对用户流失影响更大?
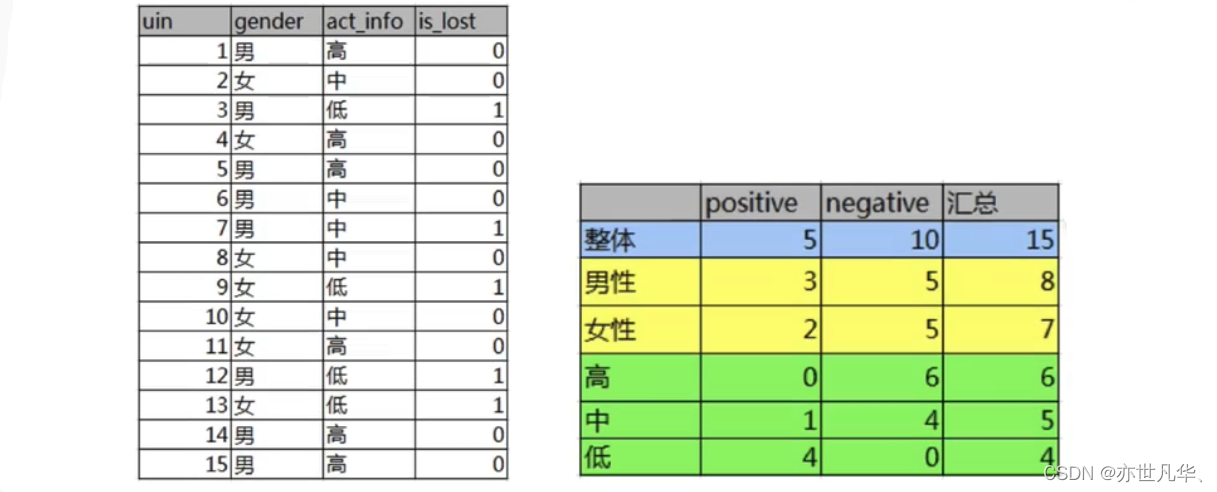
通过计算信息增益可以解决这个问题,统计上右表信息其中Positive为正样本(已流失),Negative为负样本(未流失),下面的数值为不同划分下对应的人数。可得到以下熵:

活跃度的信息增益比性别的信息增益大,也就是说,活跃度对用户流失的影响比性别大。在做特征选择或者数据分析的时候,我们应该重点考察活跃度这个指标。
信息增益率:增益率是用前面的信息增益Gain(D, a)和属性a对应的"固有值"(intrinsicvalue)[Quinlan, 1993J的比值来共同定义的。
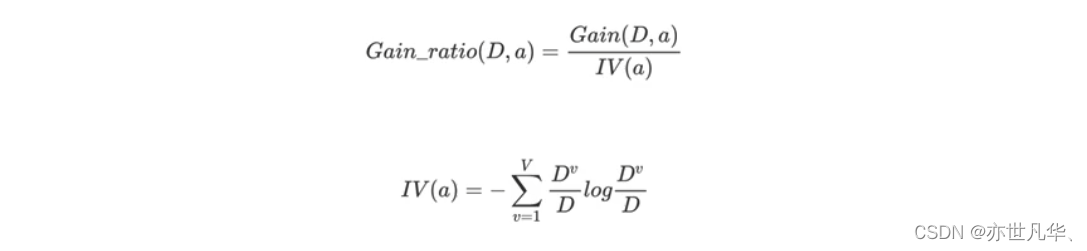
通过如下案例进行说明:如下图,第一列为天气,第二列为温度,第三列为湿度,第四列为风速,最后一列该活动是否进行。我们要解决:根据下面表格数据,判断在对应天气下,活动是否会进行?
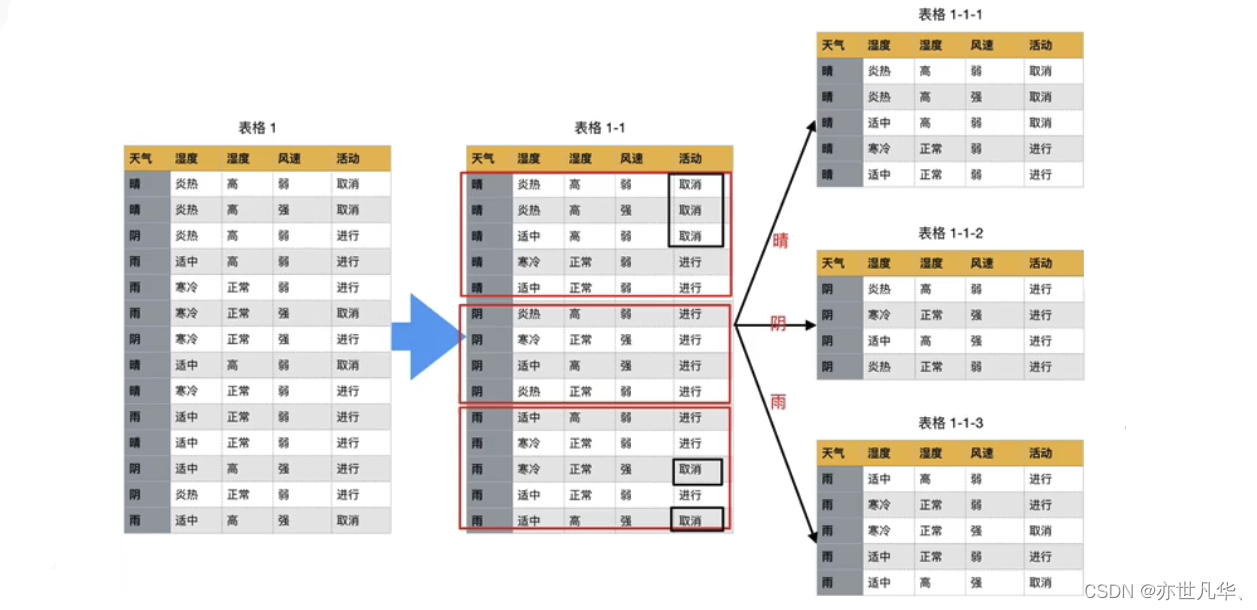
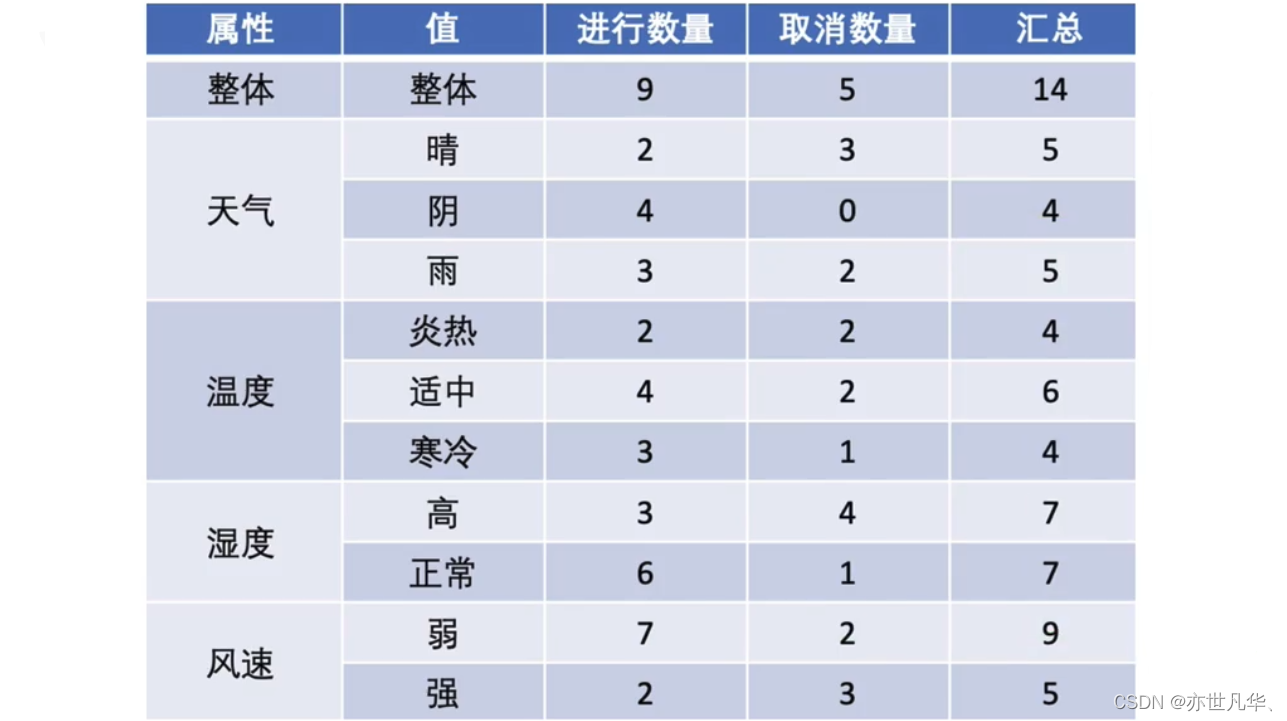
该数据集有四个属性,属性集合A={天气,温度,湿度,风速},类别标签有两个,类别集合L={进行,取消}。


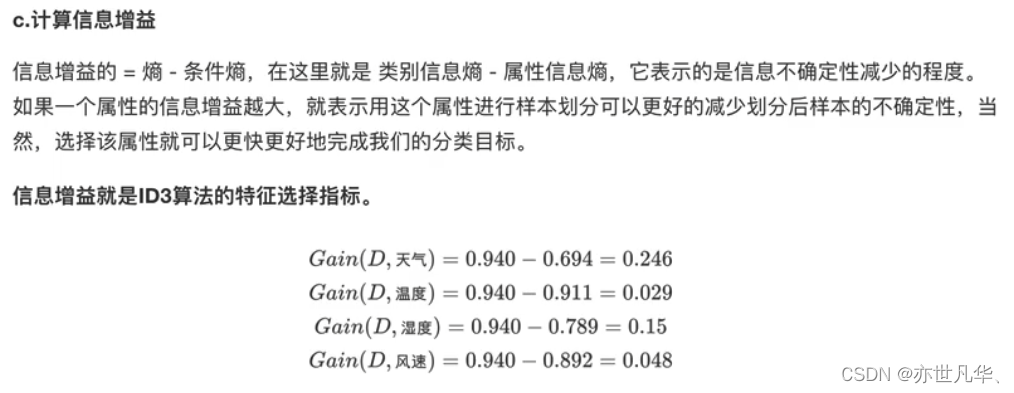


基尼系数:CART决策树[Breimanetal.,1984]使用"基尼指数”(Giniindex)来选择划分属性:
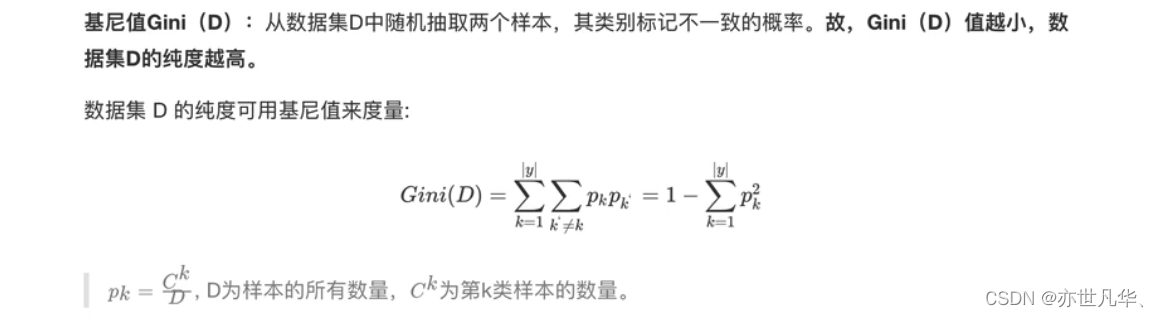

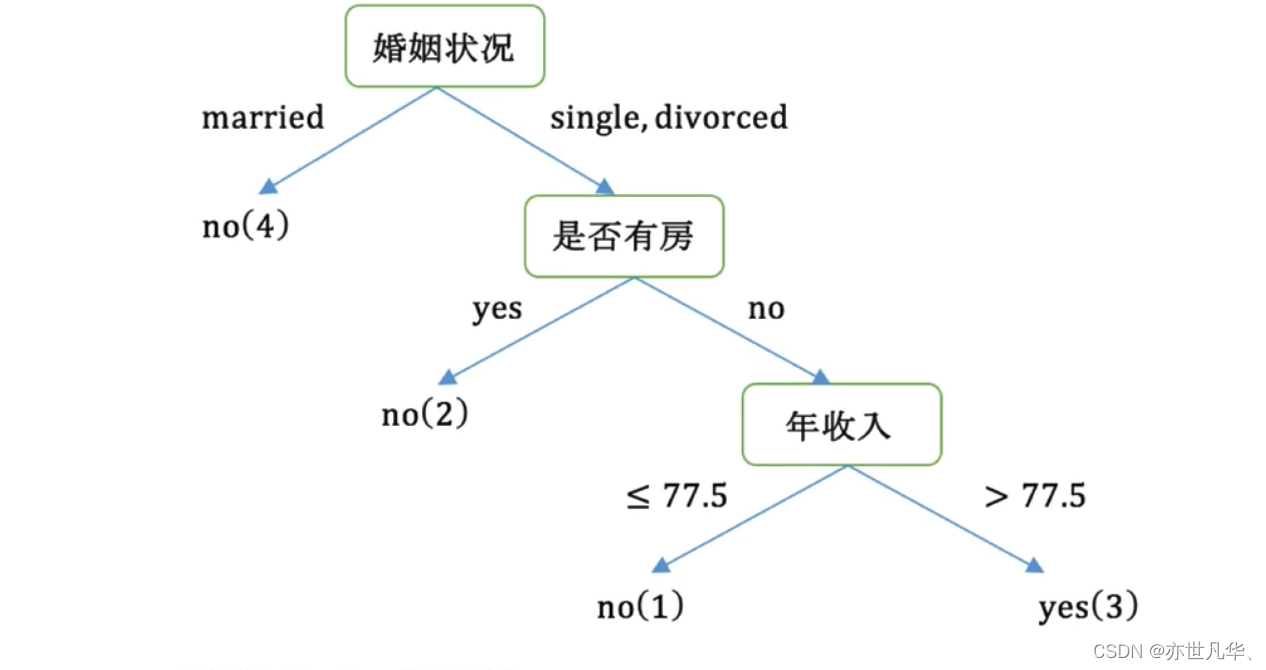
接下来根据下图列表,按照基尼指数的划分依据,做出决策树:
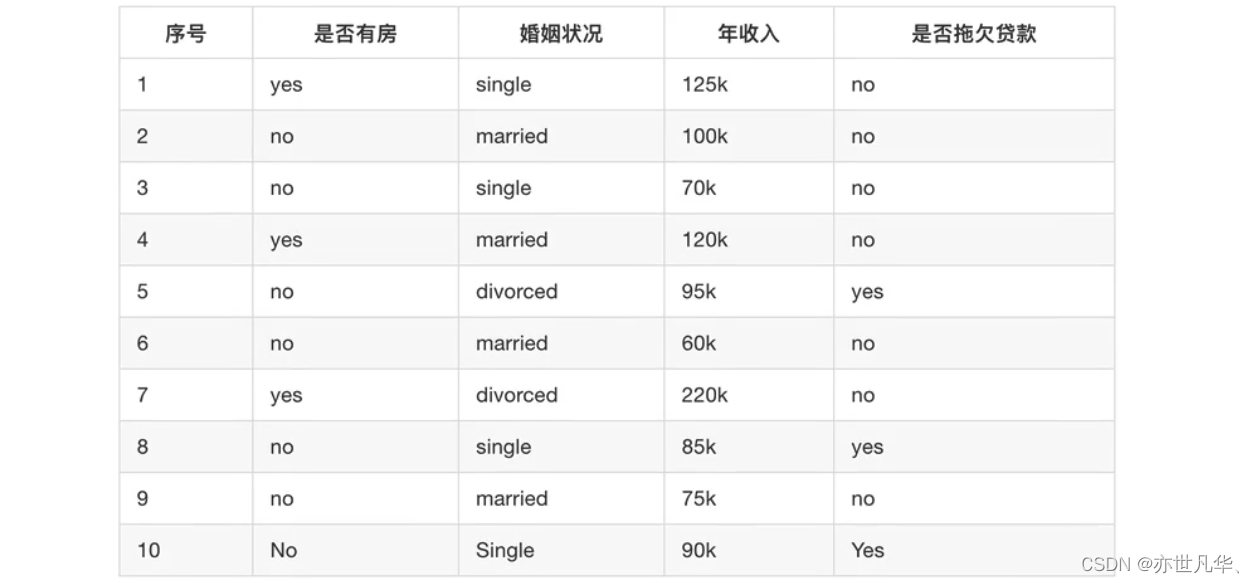
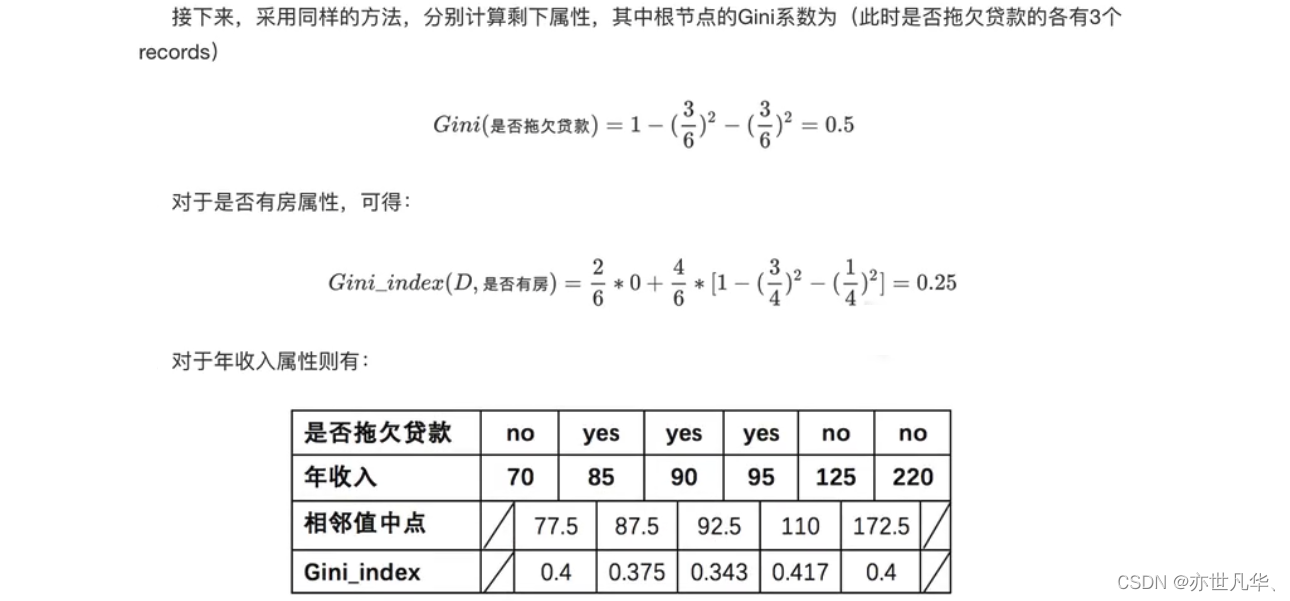
对数据集非序列标号属性{是否有房,婚姻状况,年收入}分别计算它们的Gini指数,取Gini指数最小的属性作为决策树的根节点属性。 根节点的Gini值为:
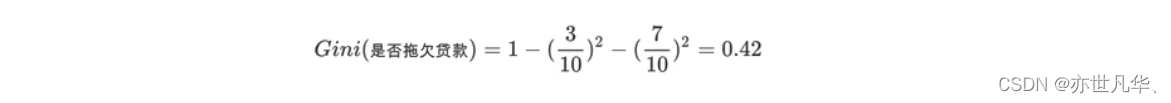
根据是否有房来进行划分时,Gini指数计算过程为:

若按婚姻状况属性来划分,属性婚姻状况有三个可能的取值{married,single,divorced},分别计算划分后的Gini系数增益:

对于年收入属性为数值型属性,首先需要对数据按升序排序,然后从小到大依次用相邻值的中间值作为分隔将样本划分为两组。例如当面对年收入为60和70这两个值时,我们算得其中间值为65。以中间值65作为分割点求出Gini指数:
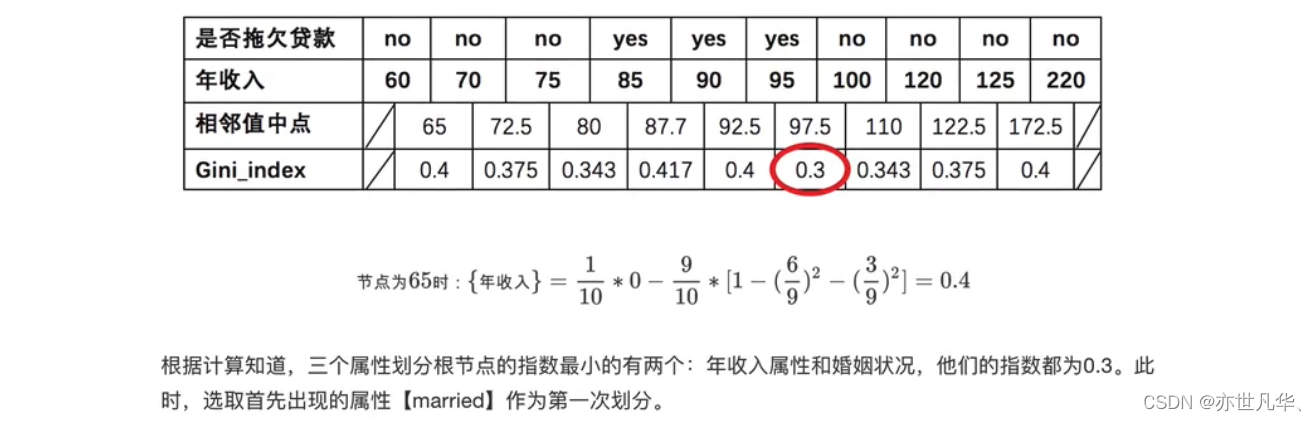
根据如上流程,构建的决策树如下图所示:
cart剪枝
CART(Classification and Regression Trees)剪枝是决策树算法中用于减小过拟合风险的一种技术。剪枝的目的是通过简化决策树的结构,使其更加泛化和适应未知数据。
剪枝(pruning)是决策树学习算法对付"过拟合"的主要手段:
在决策树学习中,为了尽可能正确分类训练样本,结点划分过程将不断重复,有时会造成决策树分支过多,这时就可能因训练样本学得“太好"了,以致于把训练集自身的一些特点当作所有数据都具有的一般性质而导致过拟合。因此,可通过主动去掉一些分支来降低过拟合的风险。
如何判断决策树泛化性能是否提升呢?
可使用前面介绍的留出法,即预留一部分数据用作"验证集"以进行性能评估。例如对下表的西瓜数据集,我们将其随机划分为两部分,其中编号为{1,2,3,6,7,10,14,15,16,17}的样例组成训练集,编号为{4,5,8,9,11,12,13}的样例组成验证集。
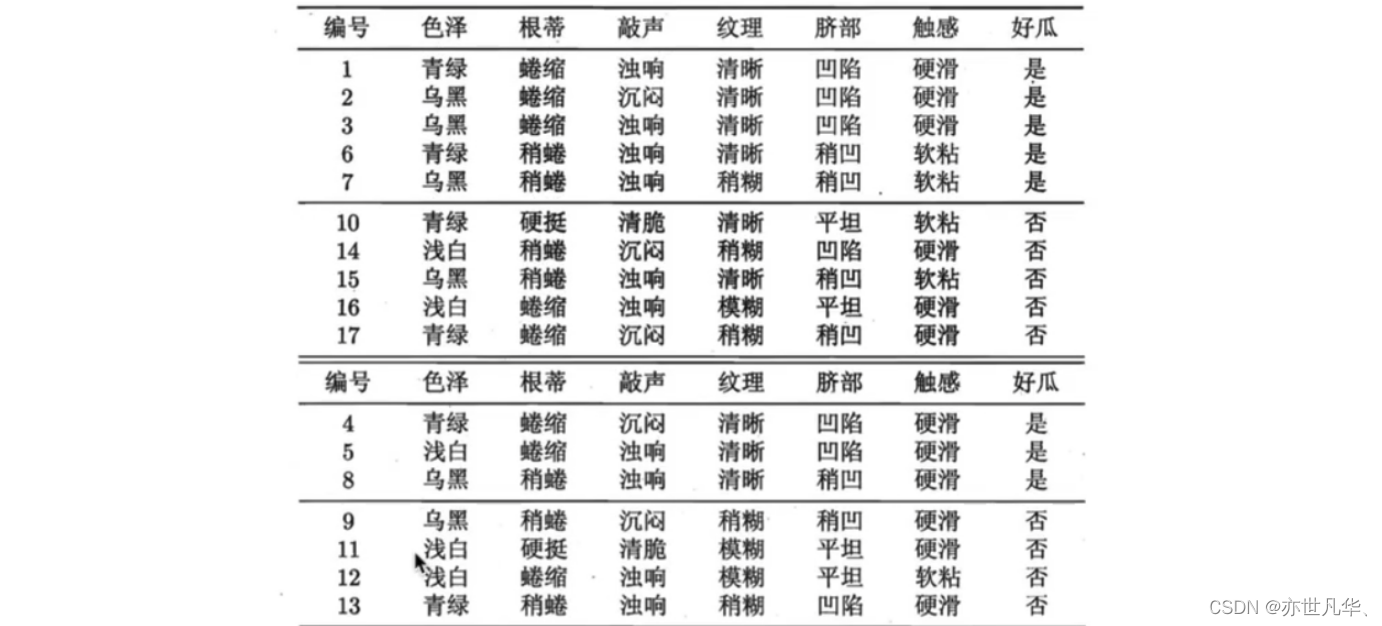
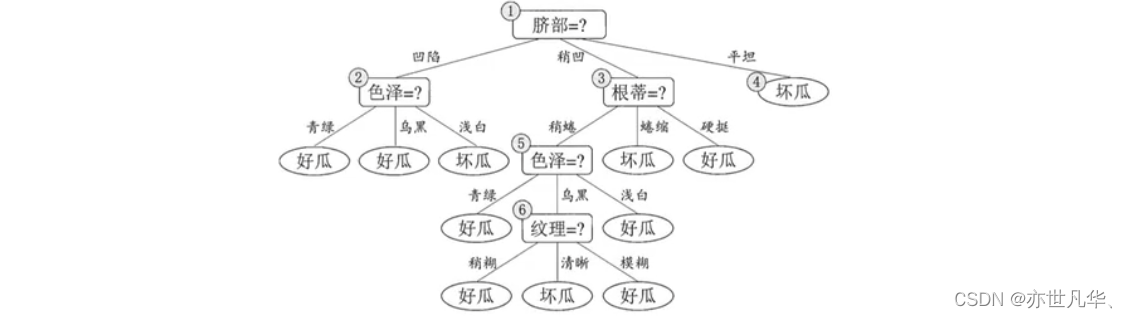
假定咱们采用信息增益准则来划分属性选择,则上表中训练集将会生成一棵下面决策树。 为便于讨论,我们对圈中的部分结点做了编号。
常用的剪枝方法:决策树剪枝的基本策略有"预剪枝"(pre-pruning)和"后剪枝"(post-pruning)。
预剪枝是指在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点
首先,基于信息增益准则,我们会选取属性"脐部"来对训练集进行划分,并产生3个分支,如上图所示,然而是否应该进行这个划分呢?预剪枝要对划分前后的泛化性能进行估计,在划分之前,所有样例集中在根结点:
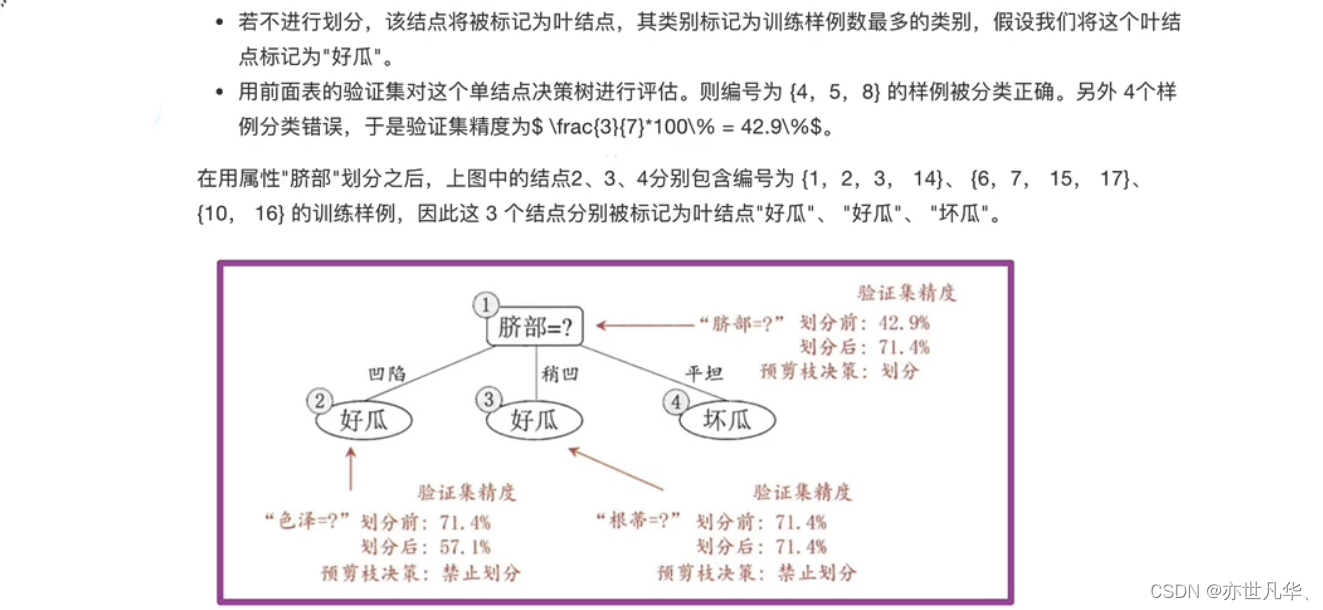

后剪枝则是先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点。
后剪枝先从训练集生成一棵完整决策树,继续使用上面的案例,从前面计算,我们知前面构造的决策树的验证集精度为42.9%:
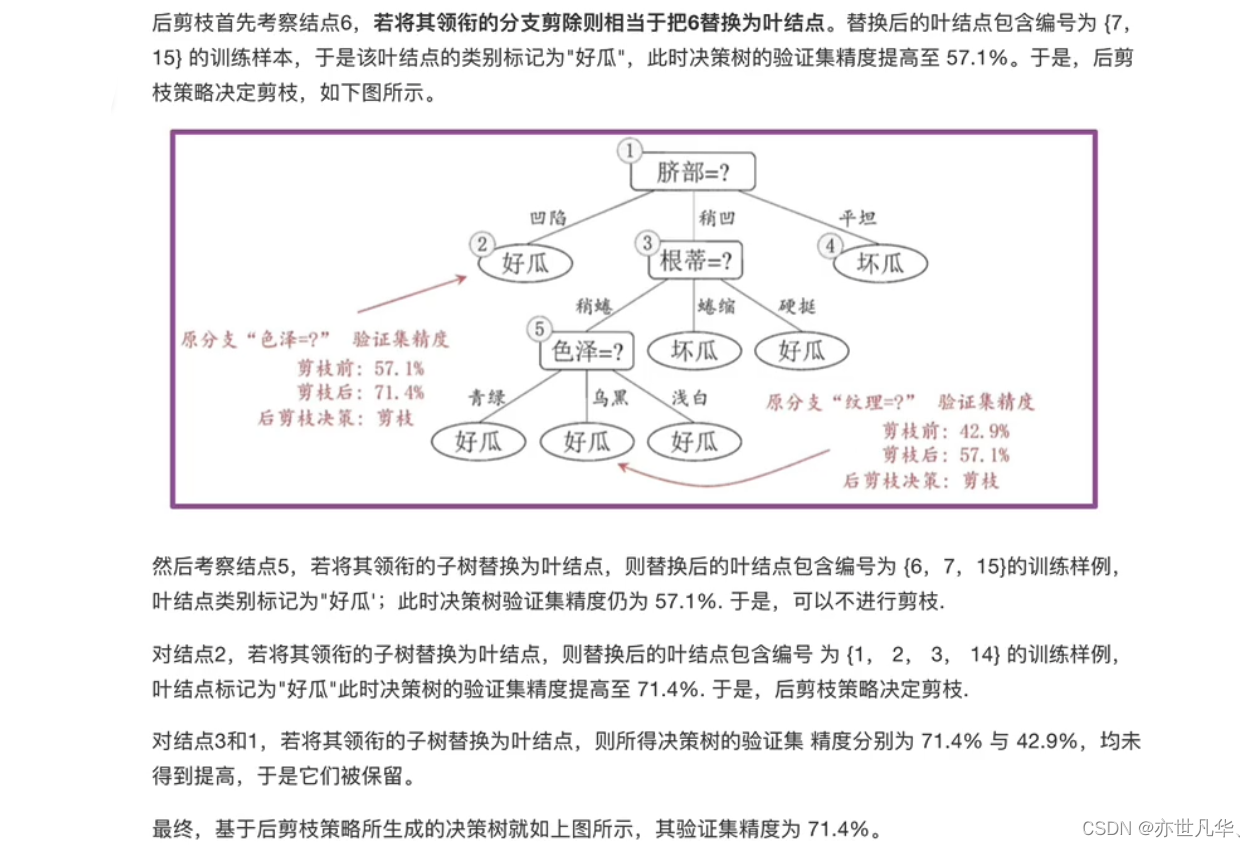
对比两种剪枝方法:
1)后剪枝决策树通常比预剪枝决策树保留了更多的分支。
2)一般情形下,后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树。
3)后剪枝过程是在生成完全决策树之后进行的。并且要自底向上地对树中的所有非叶结点进行逐一考察,因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多。
特征提取
将任意数据(如文本或图像)转换为可用于机器学习的数字特征,特征值化是为了计算机更好的去理解数据。特征提取分类主要有以下几种:
1)字典特征提取(特征离散化)
下面这段代码使用了scikit-learn库中的DictVectorizer类,实现了将字典类型的特征数据转换为数值类型的特征向量:
from sklearn.feature_extraction import DictVectorizer
def dict_demo():
# 获取数据
data = [{'city': '北京', 'temperature': 100},
{'city': '上海', 'temperature': 60},
{'city': '深圳', 'temperature': 30}]
# 字典特征提取
transfer = DictVectorizer(sparse=False) # 实例化
new_data = transfer.fit_transform(data) # 转换
print(new_data)
names = transfer.get_feature_names_out()
print("属性名字是: \n", names)
dict_demo()通过DictVectorizer类将字典类型的特征数据转换为数值类型的特征向量,并输出转换后的特征矩阵和特征名称。这种转换可以用于后续的机器学习算法输入:

2)文本特征提取
下面这段代码使用了scikit-learn库中的CountVectorizer类,实现了将文本类型的特征数据转换为数值类型的特征向量:
from sklearn.feature_extraction.text import CountVectorizer
def dict_demo():
# 获取数据
data = ["life is short, i like python", "life is too long, i dislike python"]
# 字典特征提取
transfer = CountVectorizer(stop_words=["dislike"]) # 实例化
new_data = transfer.fit_transform(data) # 转换
print(new_data)
names = transfer.get_feature_names_out()
print("特征名字是: \n", names)
dict_demo()这段代码通过CountVectorizer类将文本类型的特征数据转换为数值类型的特征向量,并输出转换后的特征矩阵和特征名称。在转换过程中,可以去除停用词,以提高特征的有效性。这种转换可以用于后续的机器学习算法输入:
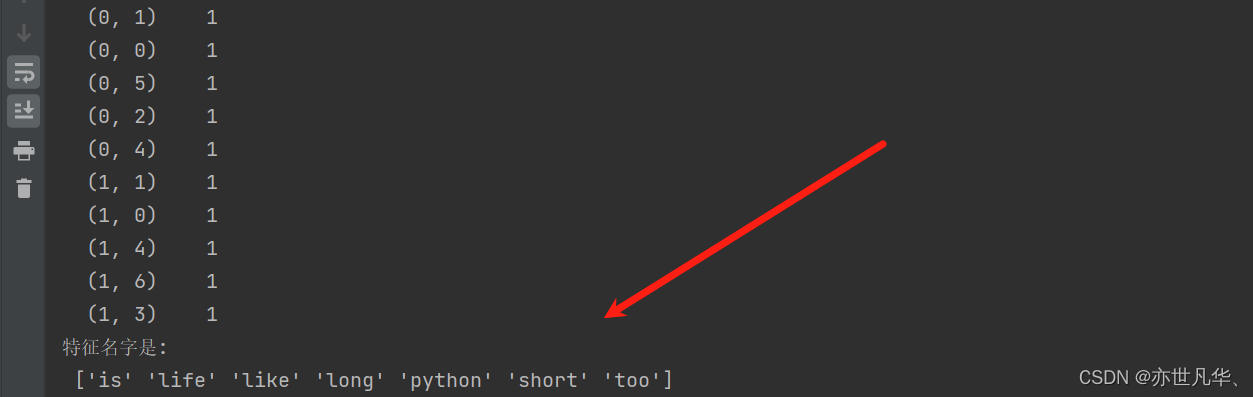
英文默认是以空格分开的。其实就达到了一个分词的效果,但是中文说话都是连贯的而不是一个一个的单词隔开,所以我们要对中文进行分词处理,这里我们需要先导入一下中文分词处理的第三方库进行安装,命令如下:
pip install pkuseg -i https://pypi.tuna.tsinghua.edu.cn/simple下面这段代码演示了如何使用 CountVectorizer 类来将文本数据转换为数值型特征。具体来说,它的功能是将每个文本转换为一个向量,其中向量的每个元素表示一个词在该文本中出现的次数:
from sklearn.feature_extraction.text import CountVectorizer
import pkuseg
def dict_demo():
# 获取数据
data = ["冬日的天空常常湛蓝无云,阳光透过稀薄的云层洒下来,给人一种温暖的感觉。",
"冬日的天空常常湛蓝无云,阳光透过稀薄的云层洒下来,给人一种温暖的感觉。阳光照在雪地上,形成晶莹剔透的冰晶,闪烁着五彩斑斓的光芒。",
"而在这样的阳光下,雪地上的痕迹清晰可见,踩在雪地上发出咯吱咯吱的声音,仿佛在向人们述说着一个个故事。"]
# 文章分割
seg = pkuseg.pkuseg() # 实例化分词器对象
list = [seg.cut(temp) for temp in data]
# 文本特征转换
transfer = CountVectorizer(stop_words=["阳光"]) # 实例化
new_data = transfer.fit_transform([' '.join(temp) for temp in list]) # 转换
print(new_data)
names = transfer.get_feature_names_out()
print("特征名字是: \n", names)
dict_demo()最终得到的结果如下:

Tf-idf文本特征提取:TF-IDF的主要思想是:如果某个词或短语在一篇文章中出现的概率高,并且在其他文章中很少出现,则认为此词或者短语具有很好的类别区分能力,适合用来分类。
TD-IDF作用:用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。

举例:
假如一篇文章的总词语数是100个,而词语“非常”出现了5次,那么”非常“一词在该文件中的词频就是5/100=0.05。
而计算文件频率(IDF)的方法是以文件集的文件总数,除以出现"非常"一词的文件数。
所以,如果“非常”一词在1,0000份文件出现过,而文件总数是10,000,000份的话,其逆向文件频率就是lg(10,000,000/1,0000)=3。最后"非常"对于这篇文档的tf-idf的分数为0.05*3=0.15
下面这段代码演示了如何使用 TfidfVectorizer 类来将文本数据转换为 TF-IDF 特征。TF-IDF 是一种常用的文本特征表示方法,它考虑了一个词在文本中的频率(Term Frequency)以及在整个语料库中的逆文档频率(Inverse Document Frequency):
from sklearn.feature_extraction.text import TfidfVectorizer
import pkuseg
def dict_demo():
# 获取数据
data = ["冬日的天空常常湛蓝无云,阳光透过稀薄的云层洒下来,给人一种温暖的感觉。",
"冬日的天空常常湛蓝无云,阳光透过稀薄的云层洒下来,给人一种温暖的感觉。阳光照在雪地上,形成晶莹剔透的冰晶,闪烁着五彩斑斓的光芒。",
"而在这样的阳光下,雪地上的痕迹清晰可见,踩在雪地上发出咯吱咯吱的声音,仿佛在向人们述说着一个个故事。"]
# 文章分割
seg = pkuseg.pkuseg() # 实例化分词器对象
list = [seg.cut(temp) for temp in data]
# 文本特征转换
transfer = TfidfVectorizer() # 实例化
new_data = transfer.fit_transform([' '.join(temp) for temp in list]) # 转换
print(new_data)
names = transfer.get_feature_names_out()
print("特征名字是: \n", names)
dict_demo()最终得到的结果如下:

3)图像特征提取(深度学习将介绍)
泰坦尼克号乘客生存预测(实操)
泰坦尼克号沉没是历史上最臭名昭着的沉船之一。1912年4月15日,在她的处女航中,泰坦尼克号在与冰山相撞后沉没,在2224名乘客和机组人员中造成1502人死亡。这场耸人听闻的悲剧震惊了国际社会,并为船舶制定了更好的安全规定。造成海难失事的原因之一是乘客和机组人员没有足够的救生艇。尽管幸存下沉有一些运气因素,但有些人比其他人更容易生存,例如妇女,儿童和上流社会。在这个案例中,我们要求您完成对哪些人可能存活的分析。特别是,我们要求您运用机器学习工具来预测哪些乘客幸免于悲剧。
我们参考kaggle平台提供的案例:网址 :
我们提取到的数据集中的特征包括票的类别,是否存活,乘坐班次,年龄,登陆home.dest,房间,船和性别等。数据来自:数据集 :
经过观察数据得到:
1)坐班是指乘客班(1,2,3),是社会经济阶层的代表。
2)其中age数据存在缺失。
接下来我们借助 jupyter 工具进行构建我们这个预测,方便我们观察:
导入需要的模块:
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier获取数据:
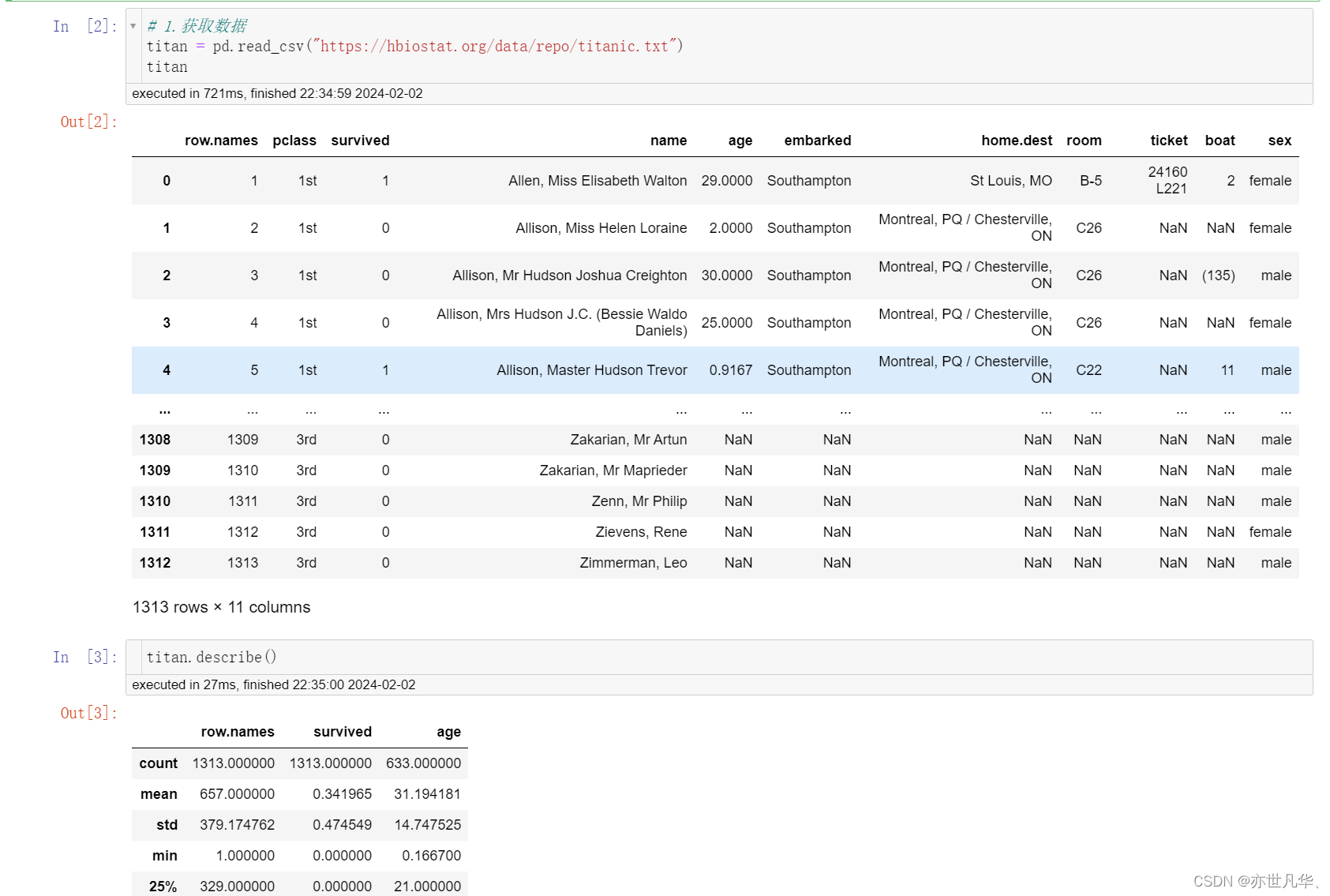
数据基本处理:
# 2.数据基本处理
# 2.1确定特征值,目标值
x = titan[["pclass", "age", "sex"]]
y = titan["survived"]
# 2.2缺失值处理
x["age"].fillna(value=titan["age"].mean(), inplace=True)
# 2.3数据集的划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22, train_size=0.2)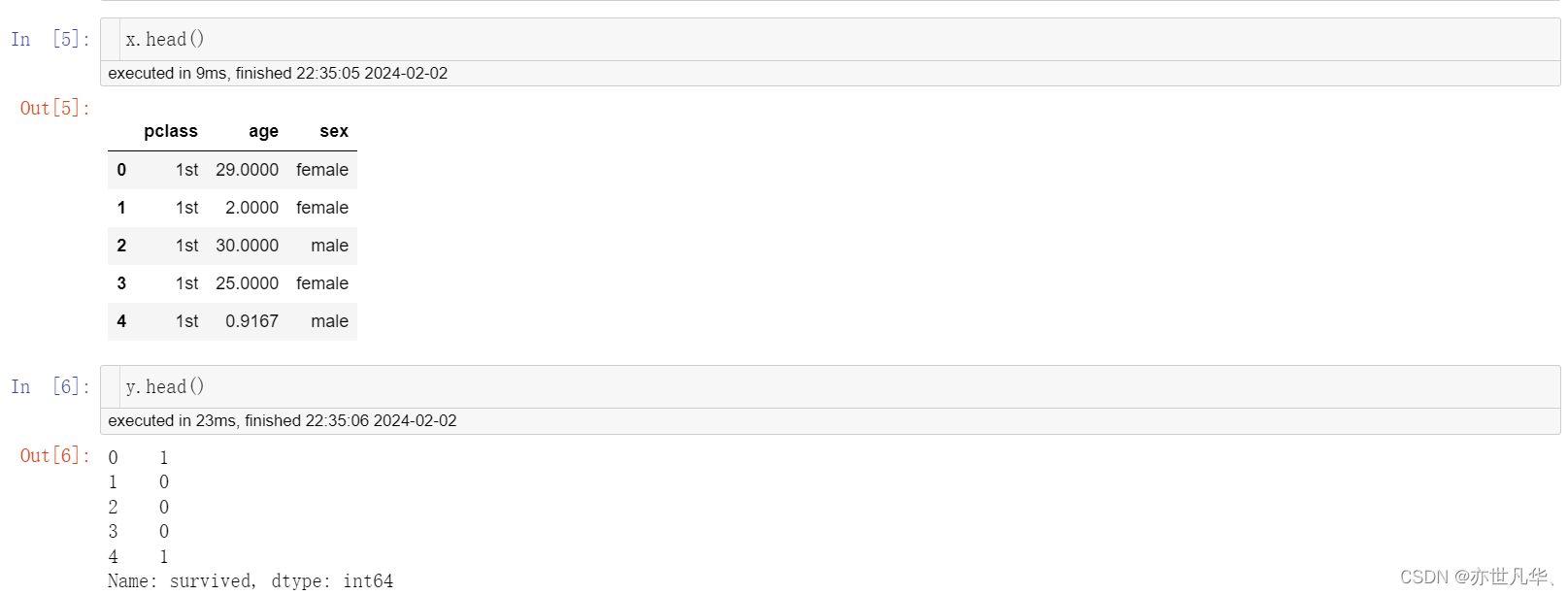
特征工程—字典特征抽取:特征中出现类别符号,需要进行one-hot编码处理(DictVectorizer)
x.to_dict(orient="records")需要将数组特征转换成字典数据
x_train = x_train.to_dict(orient="records")
x_test = x_test.to_dict(orient="records")
transfer = DictVectorizer()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
机器学习—决策树:决策树API当中,如果没有指定max_depth那么会根据信息熵的条件直到最终结束。这里我们可以指定树的深度来进行限制树的大小

模型评估:
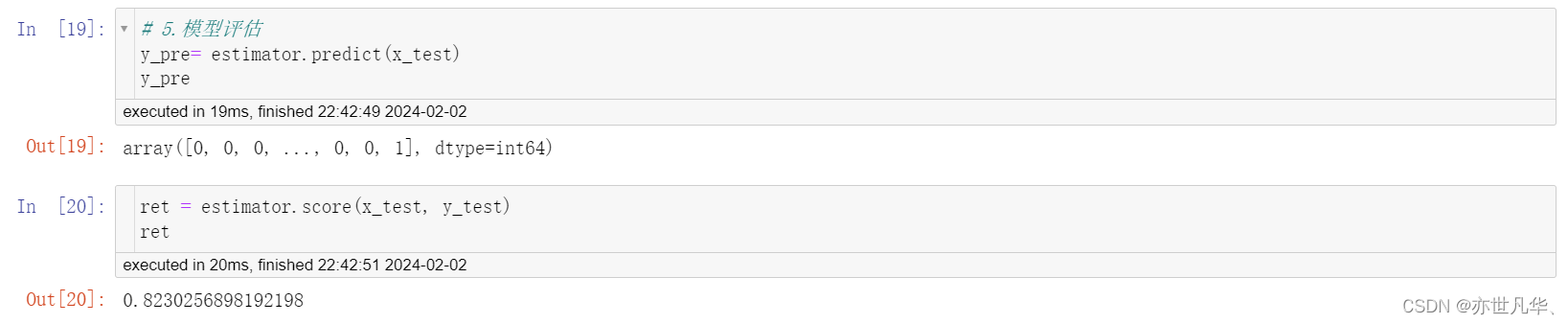
决策树可视化:通过如下的方式将我们的决策树生成的数据进行可视化:
# 导入相关库
from sklearn.tree import export_graphviz使用 export_graphviz 函数从决策树分类器 (estimator) 中导出一个可视化的决策树。
estimator: 决策树分类器对象。
out_file="tree.dot": 导出的可视化决策树将保存在名为 "tree.dot" 的文件中。该文件将在当前工作目录下创建或覆盖。
feature_names=['age', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', '女性', '男性']: 特征名称的列表。在可视化决策树时,这些特征名称将用于标记每个节点。

在生成的tree.dot文件中有如下生成的数据:

将上面tree.dot文件中的数据复制到这个网站当中:地址 ,如下生成了我们相应的决策树:
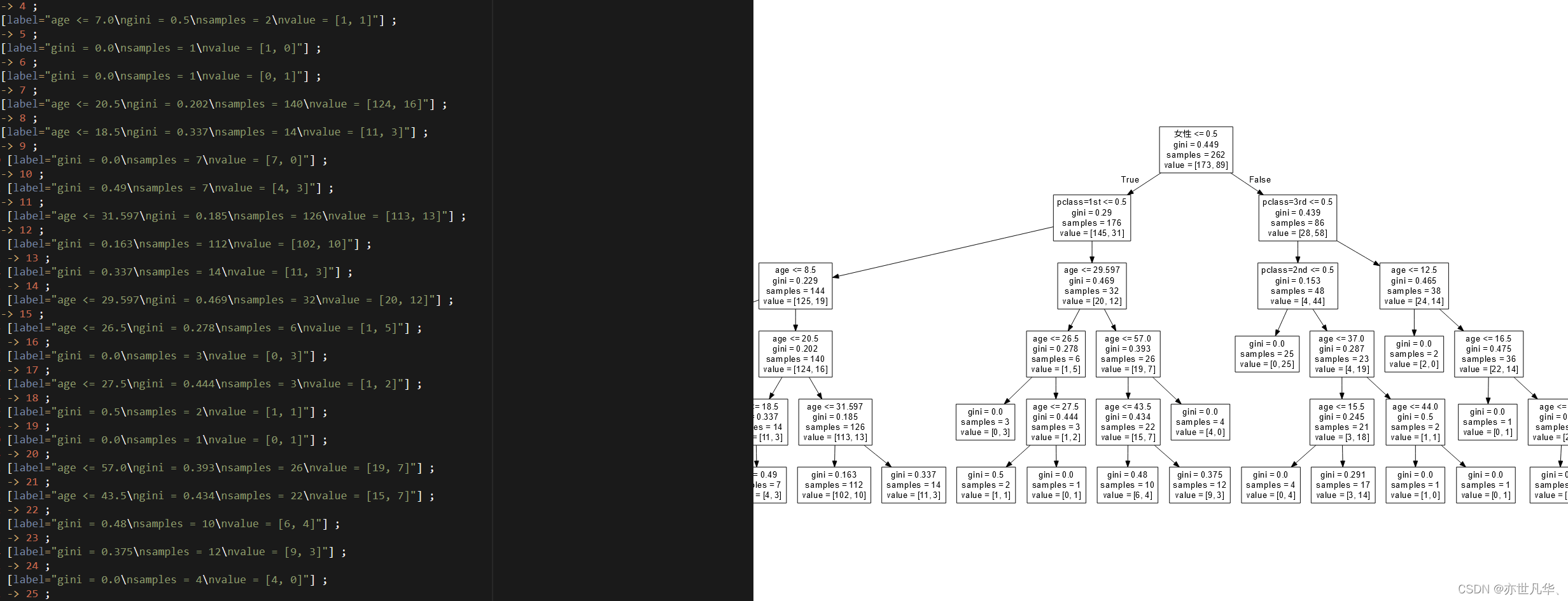
可以看到我们的决策树抛开根节点就只有五层,是因为我们在构造决策树的时候传入的最大深度就是5,这样是为了防止过拟合,当然你也可以改变数据进行测试:

总结:
优点:简单的理解和解彩树木可视化。
缺点:决策树学习者可以创建不能很好地推广数据的过于复杂的树,容易发生过拟合。
改进:(1)减枝cart算法。(2)随机森林 (集成学习的一种)
注:企业重要决策,由于决策树很好的分析能力,在决策过程应用较多,可以选择特征
回归决策树
前面已经讲到I关于数据类型,我们主要可以把其分为两类,连续型数据和离散型数据。在面对不同数据时,决策树也可以分为两大类型:
类决策树和回归决策树。前者主要用于处理离散型数据,后者主要用于处理连续型数据。
不管是回归决策树还是分类决策树,都会存在两个核心问题:
如何选择划分点?如何决定叶节点的输出值?
一个回归树对应着输入空间(即特征空间)的一个划分以及在划分单元上的输出值。分类树中,我们采用信息论中的方法,通过计算选择最佳划分点。
而在回归树中,采用的是启发式的方法。假如我们有n个特征,每个特征有si(i∈(1,n))个取值,那我们遍历所有特征,尝试该特征所有取值,对空间进行划分,直到取到特征j的取值s,使得损失函数最小,这样就得到了一个划分点。描述该过程的公式如下:

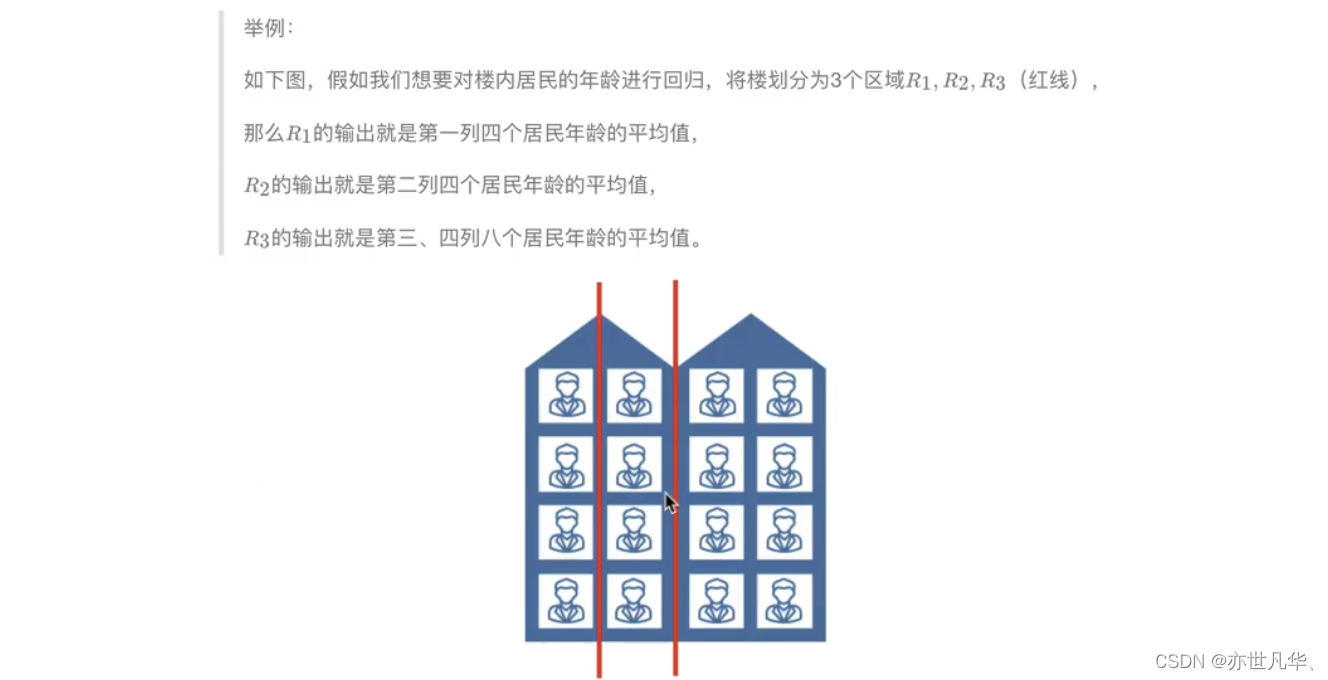
回归决策树算法描述:

为了易于理解,接下来通过一个简单实例加深对回归决策树的理解。训练数据见下表,目标是得到一棵最小二乘回归树:

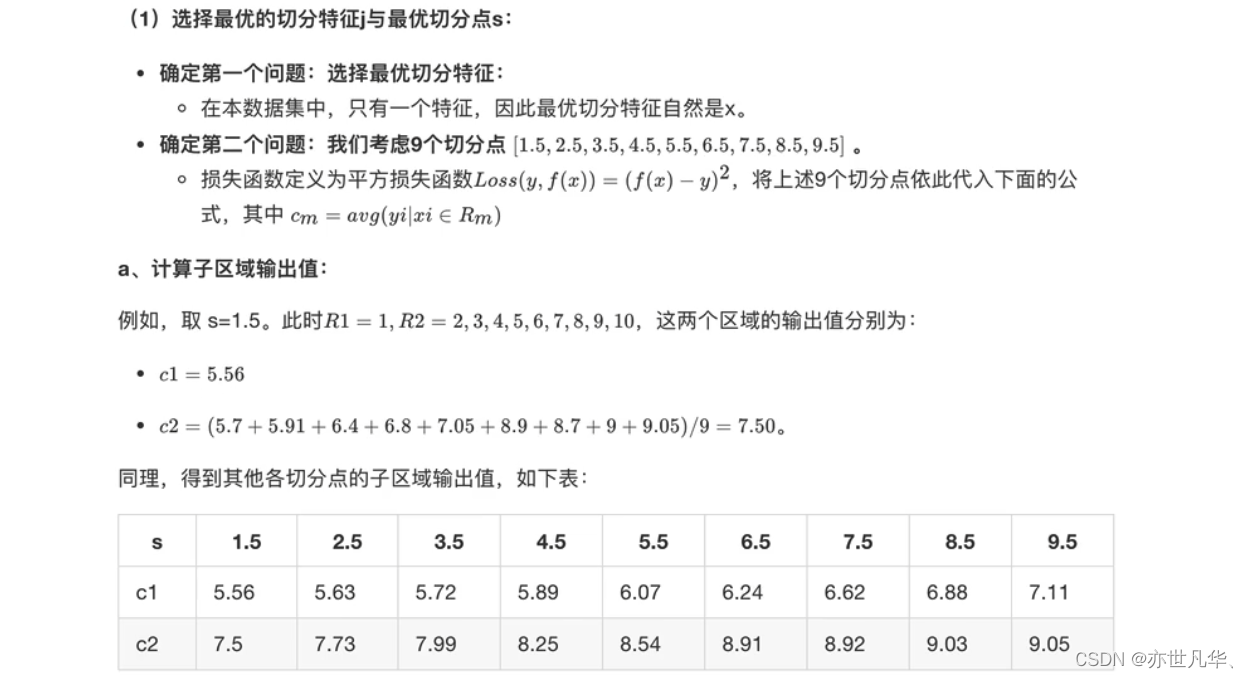
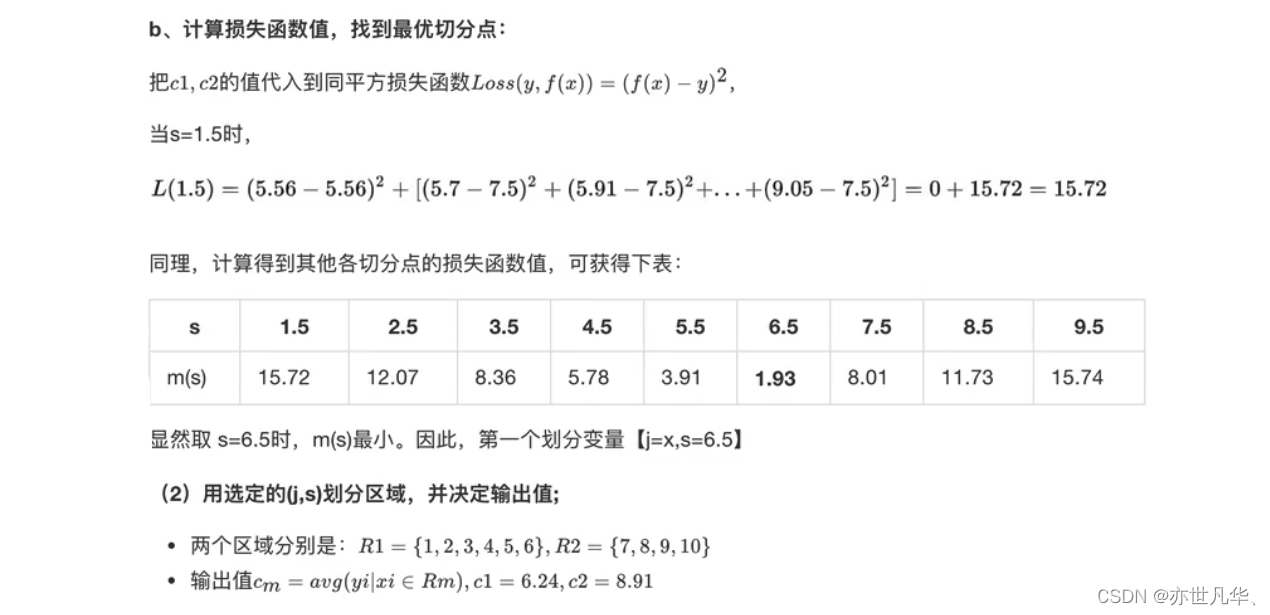
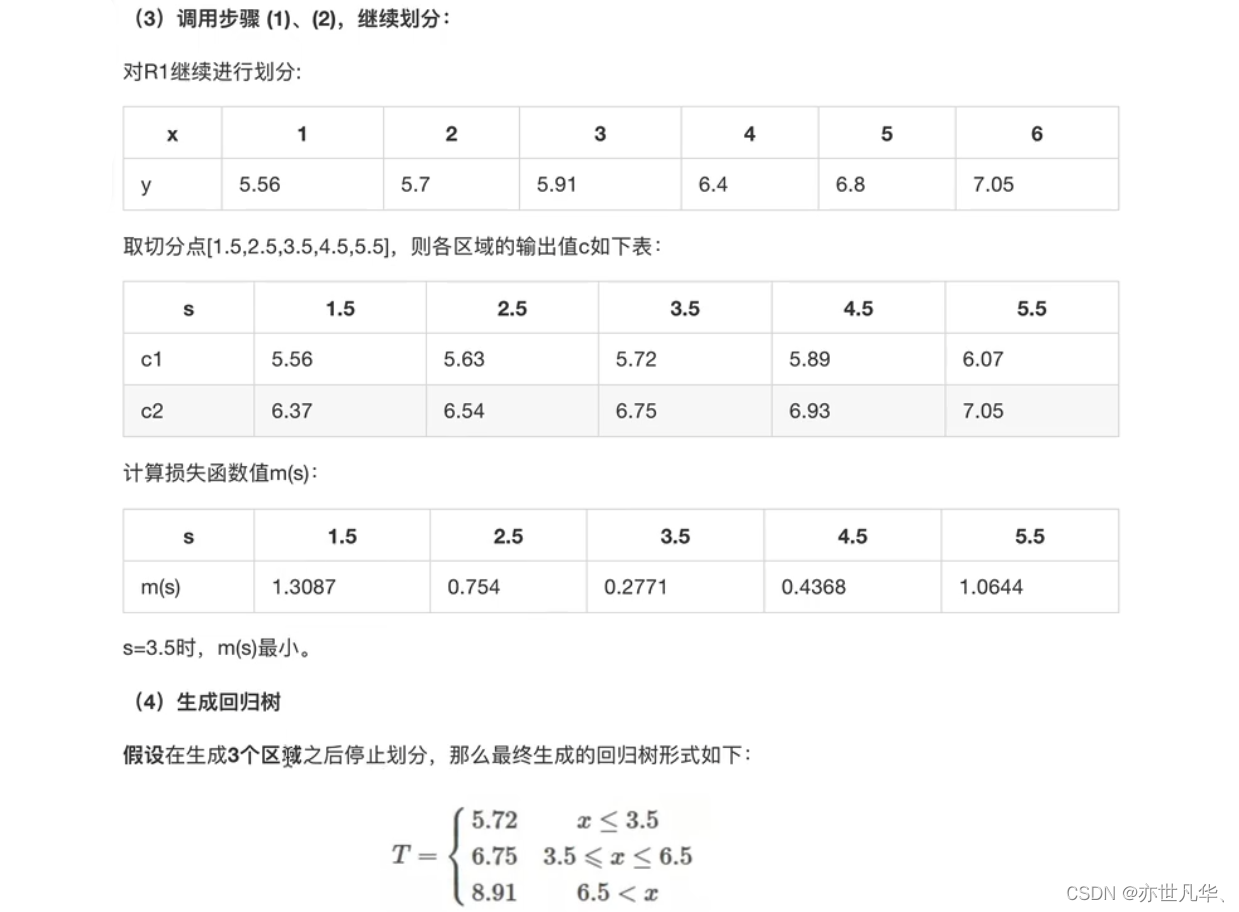
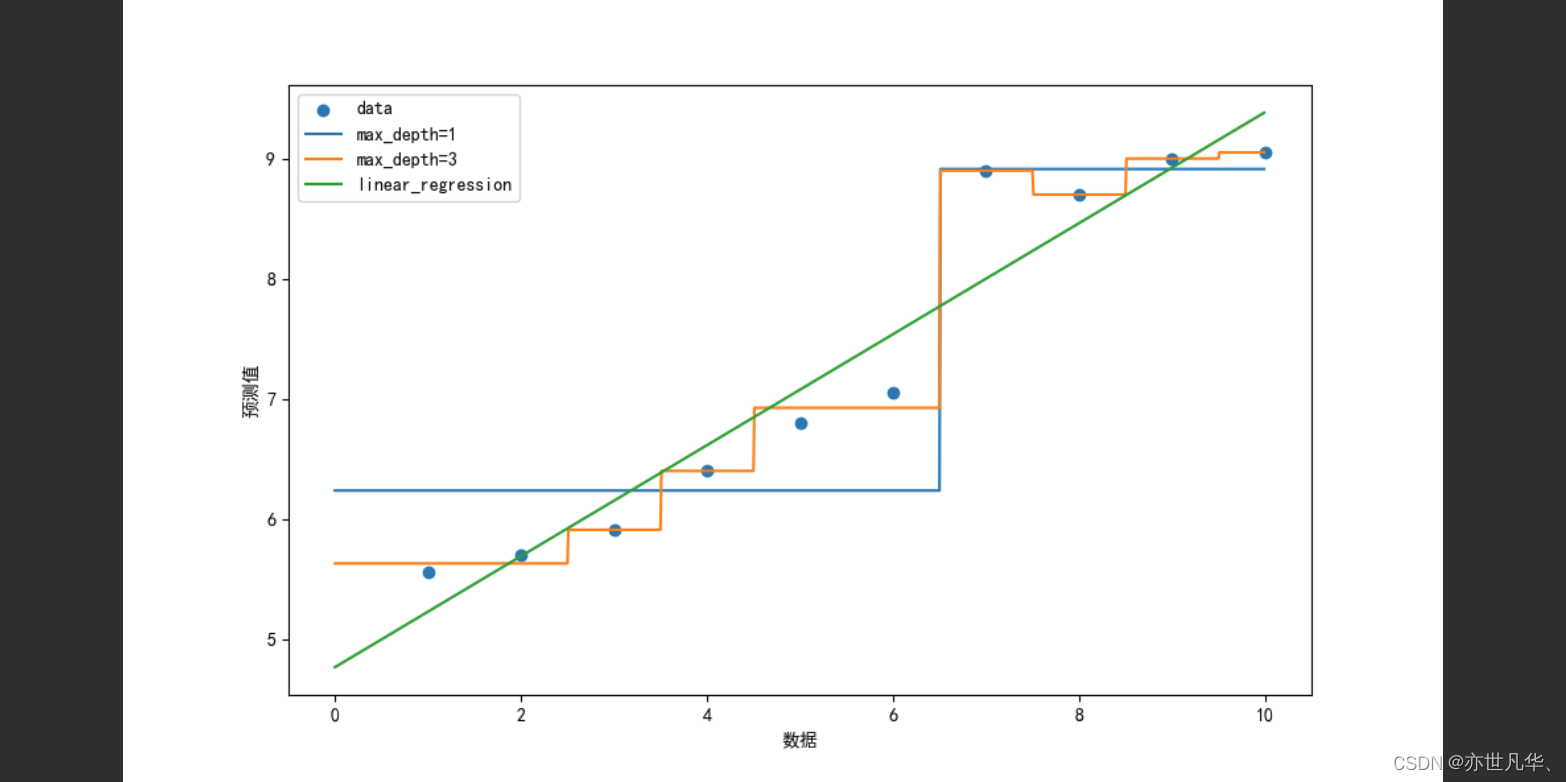
回归决策树与线性回归对比:通过下面这段代码用于比较决策树回归模型和线性回归模型在某个数据集上的预测效果,并进行可视化展示:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
from pylab import mpl
# 设置显示中文字体
mpl.rcParams["font.sans-serif"] = ["SimHei"]
# 设置正常显示符号
mpl.rcParams["axes.unicode_minus"] = False
# 生成数据
x = np.array(list(range(1, 11))).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.051])
# 模型训练
m1 = DecisionTreeRegressor(max_depth=1)
m2 = DecisionTreeRegressor(max_depth=3)
m3 = LinearRegression()
m1.fit(x, y)
m2.fit(x, y)
m3.fit(x, y)
# 模型预测
x_test = np.arange(0, 10, 0.01).reshape(-1, 1)
y_1 = m1.predict(x_test)
y_2 = m2.predict(x_test)
y_3 = m3.predict(x_test)
# 结果可视化
plt.figure(figsize=(10, 6), dpi=100)
plt.scatter(x, y, label="data")
plt.plot(x_test, y_1, label="max_depth=1")
plt.plot(x_test, y_2, label="max_depth=3")
plt.plot(x_test, y_3, label="linear_regression")
plt.xlabel("数据")
plt.ylabel("预测值")
plt.legend()
plt.legend()
plt.show()这段代码主要是用于比较决策树回归模型和线性回归模型在给定数据集上的预测效果,并进行可视化展示: