本文为 「茶桁的 AI 秘籍 - BI 篇 第 10 篇」

Hi，你好。我是茶桁。

上一节课，咱们了解了图形的具体绘制方法，接下来咱们还要看看除了图形绘制之外，还有哪些要做的可视化分析。还有一些是跟模型相关的可视化，在运算过程中我们可能会有一些模型。

来，我们先上一个例子来体验一下，包括它中间的一些数据可视化。这是一个泰坦尼克海难的一个数据示例，我们都知道这是一个著名的十大灾难之一，究竟有多少人遇难，各方统计的结果不一致。现在我们可以得到部分的数据, 数据我还是一样放在文末了。

这个数据格式是 csv 的，一共有两个文件：

• train.csv 训练集，包含特征信息，分类结果（存活与否）
• test.csv 测试集，只包含特征信息

泰坦尼克号这个练习相信以前有人做过，这是机器学习里面入门的一道经典问题。就是泰坦尼克号的乘客生存预测问题。

train 有 891 个人, 咱们来简单的看一下，这些人有一些特征。

字段	描述
Passengerld	乘客编号
Survived	是否幸存
Pclass	船票等级（有些特征标注的英文）
Name	乘客姓名
Sex	乘客性别
SibSp	亲戚数量（兄妹，配偶数）
Parch	亲戚数量（父母、子女数）
Ticket	船票号码
Fare	船票价格
Cabin	船舱
Embarked	登陆港口

有一些人当时非常幸运被打捞上来了，还有一些人就溺水死亡了。在统计这些乘客信息的时候也知道一些人当时的下落是幸存还是溺水，那我们就把这些数据用于训练。还有一些，有 500 多人下落不明。所以根据以往的预测模型来判断一下这 500 多人如果在原来的过程中到底是否死亡。

首先要做数据探索。把数据加载进来看看这个数据长什么样、有没有缺失值，有缺失值的话可能需要做补全数据。可能也有些是英文的类别，需要把它做一些编码，编码之后才能放到模型里面去，喂给模型之前也可以做一下特征选择。

可视化探索

不是所有的数据都放到模型里面，选择一些你认为重要的特征，好在可视化的过程中可以方便我们来做了解。

比如说，我们最关心的是 label 字段，就是有多少人是溺水死亡的，有多少人是幸存的。这里我们用了一个饼图：

train_data['Survived'].value_counts().plot(kind='pie', label='Survived')

我们是用Survived这个 label 去取了它的value_counts，就是求它的分布，类别特征的每一个取值的分布。然后咱们的 kind 就用 pie 的形式展现。这样就一目了然，知道大部分人应该都是溺水死亡了，0 应该就是溺水。

还可以再分析一下Pclass， 代表的是船票等级。船票等级和Survived就是幸存的人数之间的关系。

# 不同的 Pclass, 幸存人数（条形图）
sns.barplot(x='Pclass', hue='Pclass', y='Survived', data=train_data)
plt.show()

从这里的关系里面能看的出来，感觉1的 Survived 更大一点，这个 1 应该就是一等舱。所以在当时的海难事件发生过程中，如果你是一等舱，也就是最好那个船舱，那你的生存概率可以达到 60%多。二等舱的概率呢是 40%多，三等舱的概率只有 20%多。

所以从这个数据里能看出来，Pclass是一个非常关键的特征。

还有一个特征叫做Embarked,就是登陆港口。登陆港口里面也可以拿它跟Survived来做一个关联，一样，通过条形图来做个呈现。

# 不同 Embarked 幸存人数(条形图)
sns.barplot(x='Embarked', hue='Embarked', y='Survived', data=train_data)
plt.show()

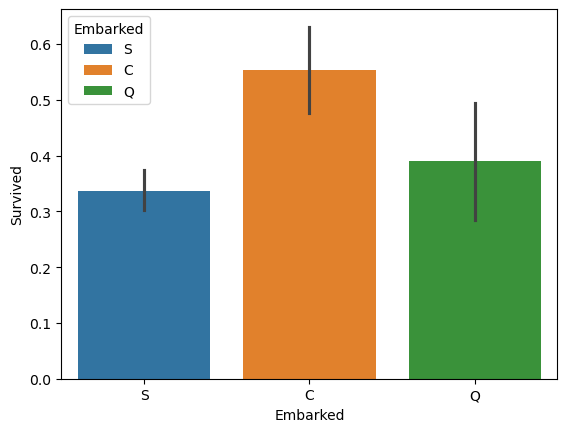
还有之前给大家讲到的热力图，热力图可以用于相关性系数的一个呈现。数据里面有很多的特征，包括男性女性、登陆港口、船票价格、年龄、船舱等级等等，大概有 10 个维度特征。这 10 个维度和其他的这些特征之间的相关性的系数可以做个计算。

# 显示特征之间的相关系数
features=['Pclass', 'Sex', 'Age', 'SibSp', 'Fare', 'Parch', 'Embarked']
train_features = train_data[features]
test_features = test_data[features]

train_data_hot_encoded = train_features.drop('Embarked', axis=1).join(train_features.Embarked.str.get_dummies())
train_data_hot_encoded = train_data_hot_encoded.drop('Sex', axis=1).join(train_data_hot_encoded.Sex.str.get_dummies())

# 计算特征之间的 Pearson 系数，即相似度
plt.figure(figsize=(10, 10))
plt.title('Pearson Correlation between Features', y=1.05, size=15)
sns.heatmap(train_data_hot_encoded.astype(float).corr(), linewidths=0.1, vmax=1.0, square=True, linecolor='white', annot=True)
plt.show()

可以看到对角线为 1， 对角线就是自己跟自己，自己跟自己之间的是完全相关的所以它为 1。

还有哪些？可以看到有些地方是非常深，也能引起注意，代表-1。这个-1 就是 male 和 female 等于-1。-1 代表什么含义是负相关，是完全反着的一个关系。

比如说如果你是 male，一定不是 female。负相关是不相关？并不是，负相关不等于不相关，负相关本身也是跟相关性是有关系的，但是它不是正向，它是反向的。

male 和 female 很明显你只能是一个，是 male 的情况下就不能是 female，所以它是一个完全的负相关。

那从这个例子里面还能找到哪些关联关系？一般会选哪些值来做判断？我们大部分人可能都会说要找那个数值高的，那个颜色浅的，深的不看。能这样看吗？这张热力图怎么判断，这张热力图要找顶部和底部的，要找绝对值最大的。

除了颜色很浅以外就是颜色很深的，可以看到负值绝对值比较大的地方颜色很深，S 和 C，这两个是一个负相关的。还可以看到 Pclass 和 Fare 之间也是一个负相关。想象一下也差不多，Fire 代表是船票的价格，船票价格越贵它的 Pclass 应该越小，等级就越高，一等舱就是最好的那个船舱价格肯定会越高。这些就可以通过相关性系数来做一个判断。

除了这种可视化后面还有一个可视化，我们用的是 Feature importance。机器学习里面有一些好处，用传统机器学习可以把特征的重要性去做一个输出。这样我们就知道在预测这个模型过程中哪些特征起到关键性的作用。

我们下面就来写一个小例子

def train(train_features, train_labels):
    # 构造 CART 决策树
    clf = DecisionTreeClassifier()
    clf.fit(train_features, train_labels)

    # 显示特征向量的重要性
    coeffs = clf.feature_importances_
    df_co = pd.DataFrame(coeffs, columns=['importance_'])

    # 下标设置为 Feature Name
    df_co.index = train_features.columns
    df_co.sort_values('importance_', ascending=True, inplace=True)
    df_co.importance_.plot(kind='barh')
    plt.title('Feature importance')
    plt.show()

    return clf

clf = train(train_data_hot_encoded, train_data['Survived'])

训练过程用的是决策树，只要把这个类实例创建好以后 fit 一下，然后就可以找到 feature importance，代表我们特征的重要性。这样我们把这个 feature importance 给它做一个排序，然后呈现出来，后面再做个可视化。然后展示了一个barh条形图，male 在整个决策树里面使用的频率会比较高，所以它是 importance，重要性比较高的。其次是 Age 等等。

然后决策树的可视化我们可以用一个包做个呈现，可以用pydotplus来呈现出来。

# 决策树可视化
def show_tree(clf):
    dot_data = StringIO()
    export_graphviz(clf, out_file=dot_data)
    graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
    graph.write_pdf('./dataset/titanic_tree.pdf')

show_tree(clf)

可以看到这张图，现在是生成了一个 PDF 的文件。这个决策树很大，我没有限制这个树的深度。

放大一点，我们可以看到它的一些细节

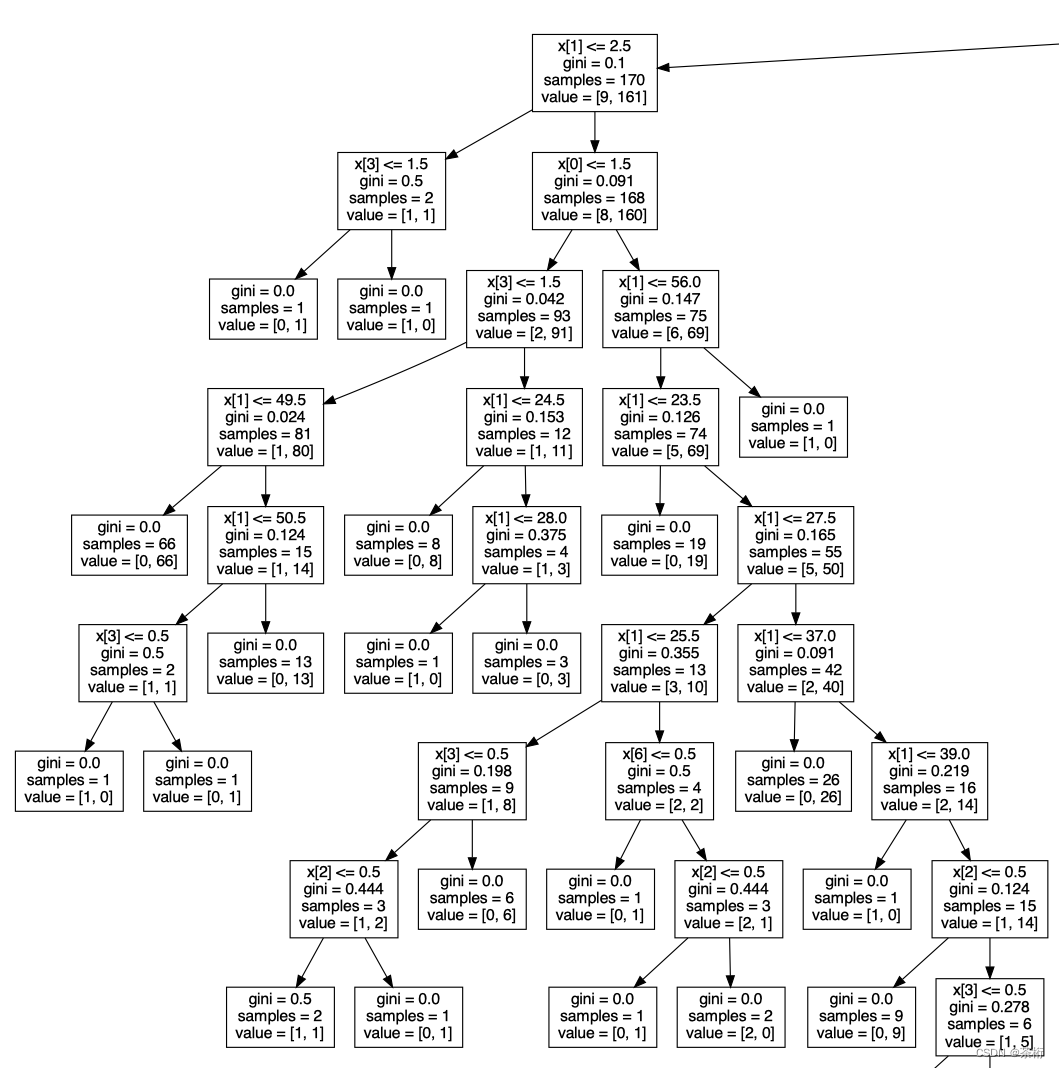
x[1]应该是等于第一个特征，跟 2.5 做个判断，如果是小于等于 2.5 就会走到左边，大于的话会走到右边。再去判断下一个值。所以它一层一层判断，就等于最后的一个叶子节点，告诉我们到底是生存还是死亡。这个就是我们决策树的一个概念。

决策树原理

之前的机器学习课程中给大家重点讲过决策树，决策树应该是属于十大经典机器学习的很重要的一个方法，一般是来做分类或者是回归值的一个预测。

举个例子，我们在这边想要做一个是否打篮球的一个分类器，我们先采集了一些数据

每条数据都有一些特征，还有一个 label 项。这个 label 就是去打篮球或者是不去打篮球。决策树就是要找到我们决策的一个依据，比如说天气作为主要依据，天气可能就会有晴天、阴天和雨天。晴天过程中，在往下又有温度、湿度和是否刮风，最后找到叶子节点，叶子结点就是最终的一个结论，去打篮球还是不去打篮球。

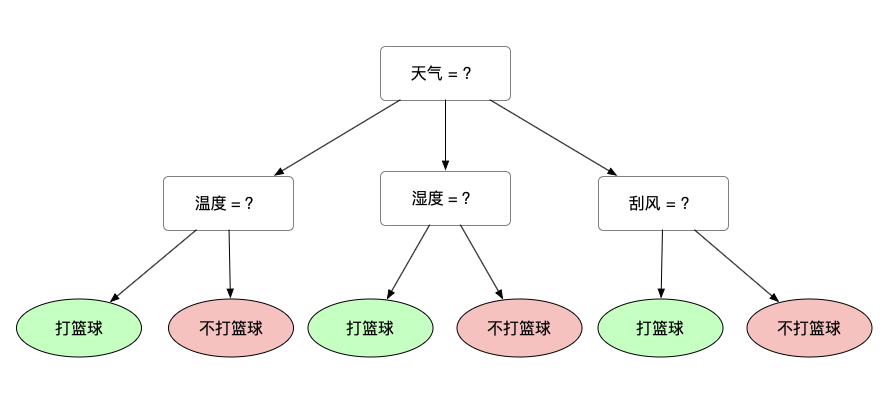
那这张图我只是画了个意思给大家看看，并不是一个严谨的决策过程。

其实在生活中也有很多决策的一些含义，有没有人以前看过一个电影叫做志明与春娇？这个电影的主人公曾经做过一次决策的时候就采用了决策树，我专门还找到了那个决策树的一个看板给大家看一下。

当时主人公想要决定到底是去约会还是不去约会，就拿这个看板，X 就是不去约会，✔️就是去约会，中间还有个循环，循环就是决策再重新走一遍。这个小球就会从上到下一直落，就会有可能落到下面一个随机的答案上。那最终就只有是和否两个决定，因为中间是重来一遍。

那其实这个看板是我们生活中可能会用到的，在分类器里就是不同的树，每一棵树的分支都是有明确的含义的，要找到属性的判断的依据。一般来说许多树是两个 XY，就是「是和否」这两个。

那决策树怎么去做判断？决策树里面的节点有根节点，内部节点和叶子节点。想要构造这棵数的时候在思考的问题就是哪一个属性作为根节点，中间的这个属性怎么去选。这个过程中会用到一个叫做信息的概念。决策树的分裂，构造这棵树就是要找这种纯净划分的过程，也就是说让目标分歧最小化，大家的结论尽量的一致。也就是说，「纯」就是让目标变量的分歧最小，这种方式，我们认为构造是更合理的。比如说：

• 集合 1: 6 次都去打篮球
• 集合 2: 4 次去打篮球，2 次不去打篮球
• 集合 3: 3 次去打篮球，3 次不去打篮球

第一个集合就是这个集合的叶节点是 6 次都去打篮球，6 个样本每个样本的结论都是打篮球。第二个也是 6 个样本，4 个打篮球 2 个不打。第三个的是 3 个打篮球，3 个不去打篮球。那么请问，如果按照纯净程度来划分哪一个集合的纯净度会更高呢？很明显的集合 1，6 个都是打篮球没有分歧，所以第一个纯净度更高。其次是第二个，最差的是第三个，因为大家的分歧最大。

我们就简单给大家说一下这个原理，有的时候如果你要去面试对方是一个传统企业，用到决策树的话有可能会问到。

决策树算法

决策树就是找纯净划分，所以我们先需要用一个统计量去计算纯净度。这里用的一个统计量叫做信息熵，信息熵的概念代表的是信息的不确定度，不确定度正好是跟纯净度相反，提升纯净度的另一个含义就是降低信息熵。

在信息论中，随机离散时间出现的概率存在着不确定性，为了衡量这种信息的不确定性，香农引入了信息熵。

$$\begin{array}{r}Entropy(t)=-\sum _{i=0}^{c-1}p(i|t)lo{g}_{2}p(i|t)\end{array}$$

这里 p(i|t)代表了节点 t 为分类 i 的概率，$lo{g}_2$ 为以 2 为底的对数。

决策树就要去分裂，分类特征有很多种可能性，我们把所有的可能性都做一个遍历，找到那一个信息熵可以降低的，这样不确定性不就少了吗。

所以就是选择第一个，我们可以来简单计算下就知道，这次我们不用上面的三个集合，重新假设 2 个集合，因为第一个集合太纯净了，我们掺入一些不确定性再来看：

• 集合 1: 5 次去打篮球，1 次不去打篮球
• 集合 2: 3 次去打篮球，3 次不去打篮球

计算下来，集合的信息熵：

$$\begin{array}{rl}Entropy(t)& =-(\frac{1}{6})lo{g}_2(\frac{1}{6})-(\frac{5}{6})lo{g}_2(\frac{5}{6})=0.65\\ Entropy(t)& =-(\frac{3}{6})lo{g}_2(\frac{3}{6})-(\frac{3}{6})lo{g}_2(\frac{3}{6})=1\end{array}$$

可以看到，第一个集合的信息熵为 0.65， 第二个集合的信息熵为 1，集合 2 的信息熵更大一些，信息熵越大，就表示不确定性越强,所以集合 1 就会更好一点。

这个就是决策树的原理，这里就不详细的展开。之前咱们机器学习的课程里有两节专门将决策树和随机森林，大家可以去仔细的学习下。

• 16. 机器学习 - 决策树
• 17. 机器学习 - 随机森林

现在只需要知道它背后是采用了一个纯净度的划分的标准。

决策树有三种算法，比较常见的 ID3、C4.5 和 CART 算法，这三种算法都是要去找纯净划分。但这三种也有些区别，ID3 要找信息增益，也就是 Gain 值，就是信息不确定性下降最快的那一个。信息增益 Gain = 父亲节点的信息熵 - 分裂后字节点的信息熵。Gain > 0, 说明信息熵下降。

C4.5 做的不是一个绝对值的，做的是个比值。因为 ID3 虽然方法简单，但是它有可能带来一个问题，就是把数值类型很多的属性倾向于做优先的选择。

如果我们把 ID 放到模型里面来做训练，ID 代表每个样本的 ID，第一条数据比如说 ID 等于 1，第二条数据 ID 等于 2，请问这个 ID 的属性对于我们打篮球的决策有没有判断价值呢？放到模型里面应该是没有价值，我们不能把 ID 放进去。但是对 ID3 来说它会倾向于选择这样的属性。

那么怎么样做改进呢？就在 C4.5 里面做的改进，它把信息增益率放进去了。因为属性值很多，增益大了，属性熵更大，所以它新增益率反而是小的。

信息增益率 = 信息增益 / 属性熵

这样，我们在 C4.5 里面就不会选择那个属性值多的。

以上这些就是决策树的概念，可以把它理解成为我们一个判断的标准，通过找属性让信息的纯度更加的纯净一点。

决策树可视化

如果你要绘图的话，要做决策树的看板就要使用到一个工具包，通过 pydot 和 GraphViz 实现决策树的可视化，把图的分裂情况做个呈现。

pip install graphviz

那到这里，我们就把决策树给大家讲完了。其实决策树只要知道它背后的逻辑是按照数的分叉来去走的，想象一下那个《志明与春娇》那个看板就可以了。

一般也很少有人把树打印出来。因为绝对数它往往很大，如果你有十几二十层的话把它打印出来了也很难去理解它的内部构造。所以通常我们只要知道它是一个有逻辑性的一个可视化的分类过程就可以了。

泰坦尼克海难数据

链接: https://pan.baidu.com/s/1ze8eJnhNYoqOEg5XZkG3CA?pwd=qkma 提取码: qkma
–来自百度网盘超级会员 v7 的分享