77. 组合

题目链接：组合

题目描述：
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。

解题思路：
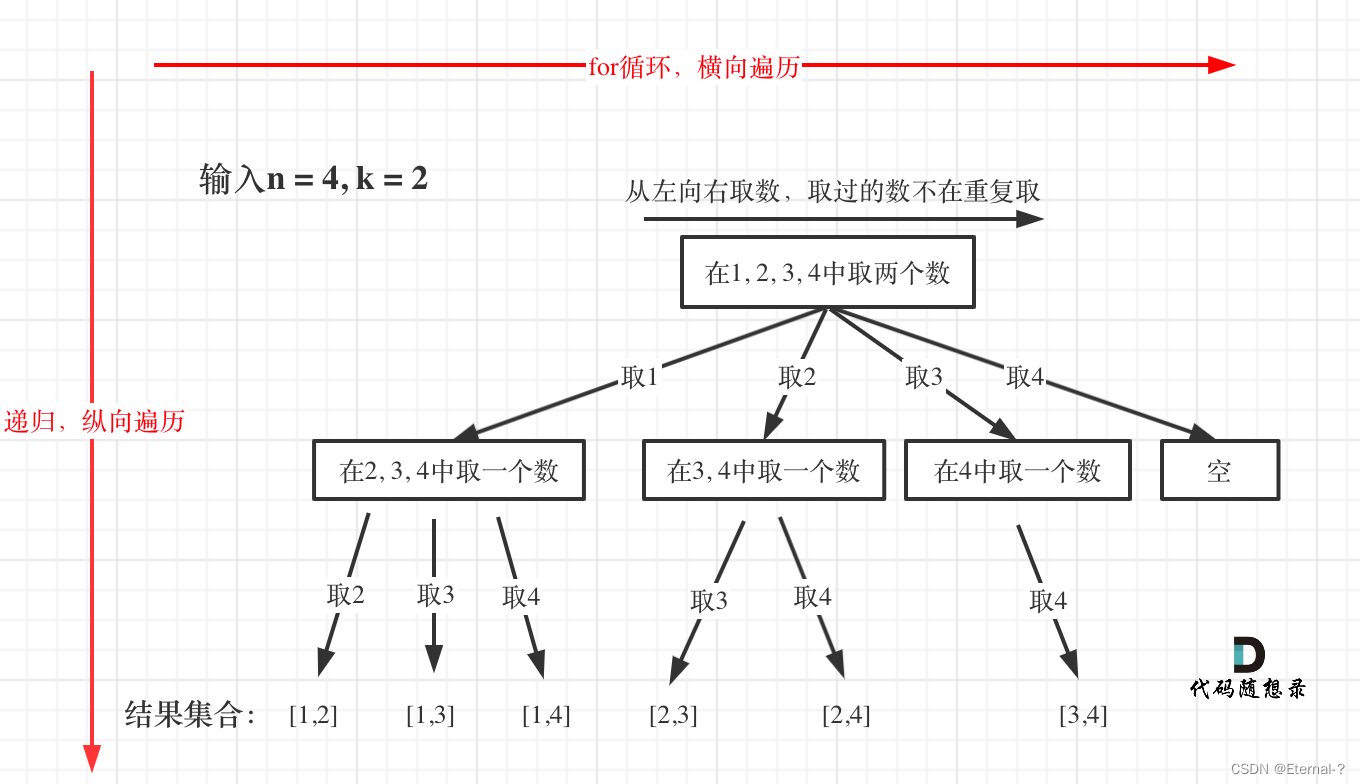
本题是经典的回溯法解决的组合问题，回溯问题搞清楚纵向递归横向遍历即可，从题目可以看出横向是选取一个数，纵向是递归选取下一个数，如图所示。
因此按照卡哥的回溯模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

即可简单的写出此题的回溯算法。

此题的剪支可以从剩下的数字不足凑够k个数来进行剪支

代码实现：
未剪支

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new LinkedList<>();

    public List<List<Integer>> combine(int n, int k) {
        backtracking(n+1,k,1);
        return res;
    }

    public void backtracking(int n, int k, int begin) {
        if (k == 0) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = begin; i < n; i++) {
            path.add(i);
            backtracking(n,--k,i+1);
            path.removeLast();
            ++k;
        }   
    }
}

剪支

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new LinkedList<>();

    public List<List<Integer>> combine(int n, int k) {
        backtracking(n+1,k,1);
        return res;
    }

    public void backtracking(int n, int k, int begin) {
        if (k == 0) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = begin; i < n-k+1; i++) {//修改此处i的范围为n-k+1
            path.add(i);
            backtracking(n,--k,i+1);
            path.removeLast();
            ++k;
        }   
    }
}