在现代多核处理器的时代,有效地利用并行计算可以极大地提高程序的性能。Java中的ForkJoin框架是Java 7引入的一个并行计算框架,它提供了一种简单而高效的方式来利用多核处理器。在本文中,我们将深入探讨ForkJoin框架的原理和工作方式。
一、什么是ForkJoin框架?
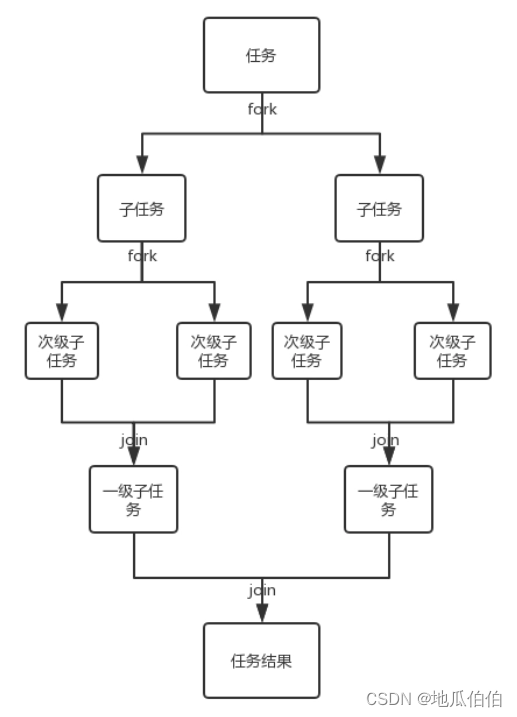
ForkJoin框架是Java并发包(java.util.concurrent)的一部分,主要用于并行计算,特别适合处理可以递归划分成许多子任务的问题,例如大数据处理、并行排序等。该框架的核心思想是将一个大任务拆分成多个小任务(Fork),然后将这些小任务的结果汇总起来(Join),从而达到并行处理的效果。
二、ForkJoin框架的核心组件
1. ForkJoinPool:
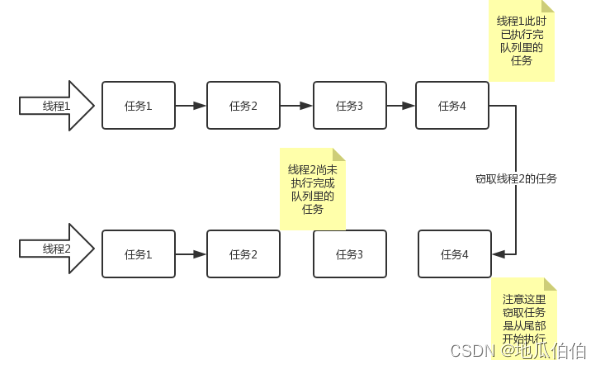
- 这是执行ForkJoin任务的线程池。线程池中的每个线程都有一个自己的任务队列,当一个线程完成了它的任务后,它会尝试从其他线程的任务队列中“窃取”任务来执行(称为工作窃取(Work-Stealing)的算法)。这种机制有助于平衡负载,使得所有线程都能保持忙碌状态,从而提高 CPU 的利用率。
在工作窃取算法的实现过程中,ForkJoinPool会维护一个优先级队列(priority queue),用于存储等待被窃取的任务。每个工作线程都会维护着一个优先级队列,并使用优先级队列来实现工作窃取。当一个新任务到达时, ForkJoinPool会根据任务的优先级将任务分配给一个空闲的工作线程进行处理。如果所有的工作线程都忙碌或没有空闲状态,则该任务会被加入到优先级队列中等待处理。
需要注意的是,虽然工作窃取算法可以提高并行计算的效率,但它也可能带来一些负面影响。例如,如果某个工作线程一直处于忙碌状态而无法进行窃取操作,那么其他工作线程可能会因为缺乏任务而陷入等待状态,导致执行效率降低。因此,在使用工作窃取算法时需要根据具体情况进行调整和优化。
-
ForkJoinPool特别适合处理可以递归划分成许多子任务的问题,如大数据处理、并行排序等。开发者需要定义一个ForkJoinTask(通常是RecursiveAction或RecursiveTask的子类),并实现其compute方法,在该方法中描述任务的划分和执行逻辑。
-
在应用场景方面,ForkJoinPool适合在有限的线程数下完成有父子关系的任务场景,比如快速排序、二分查找、矩阵乘法、线性时间选择等场景,以及数组和集合的运算。
总的来说,ForkJoinPool通过其特有的fork和join机制以及工作窃取算法,提供了一种简单而高效的方式来利用多核处理器进行并行计算
2. ForkJoinTask:
-
ForkJoinTask通常是一个需要并行处理的任务,但它比传统的线程更轻量级。大量的任务和子任务可以存在于少量的实际线程中,因为ForkJoinTask使用了一种高效的线程管理策略。主ForkJoinTask被明确提交到ForkJoinPool后开始执行,或者没有参与ForkJoin计算,开始于ForkJoinPool.commonPool()。一旦启动,它通常会启动其它的子任务。
-
ForkJoinTask有两个重要的子类:RecursiveAction和RecursiveTask。RecursiveAction用于执行没有返回值的任务,而RecursiveTask用于执行有返回值的任务。这两个子类都需要实现一个compute()方法来定义任务的逻辑。
-
ForkJoinTask中的fork()方法用于将任务放入队列并安排异步执行,而join()方法则用于等待计算完成并返回计算结果。这些方法使得任务的分解和合并变得非常简单和高效。
三、 ForkJoin框架的工作原理
1. 任务划分(Fork):
- 开发者需要定义一个ForkJoinTask(通常是RecursiveAction或RecursiveTask的子类),并实现其compute方法。
- 在compute方法中,任务应该被检查是否可以进一步细分。如果可以,应该使用fork方法将其细分为子任务。
- fork方法会异步地执行子任务,这意味着子任务会在ForkJoinPool中的一个线程上执行,而不会阻塞当前线程。
2. 任务执行和结果合并(Join):
- 当一个任务无法再细分时,它应该开始执行其实际的工作。
- 对于有返回值的任务(RecursiveTask),任务完成时需要返回其结果。
- 其他任务可以使用join方法等待一个子任务完成,并获取其结果(仅适用于RecursiveTask)。
- join方法是阻塞的,它会等待子任务完成。但是,由于ForkJoinPool使用了工作窃取算法,即使一个线程在等待子任务完成,它也可以执行其他任务,从而保持CPU的忙碌状态。
四、ForkJoin的使用
1. 先看下fork/join在stream中的应用:
Fork/Join框架在Java Stream API中有广泛的应用,尤其是在并行流(parallel streams)中。Stream API是Java 8引入的一种新的数据处理方式,它允许开发者以声明式的方式处理数据集合,如转换、过滤、映射、归约等操作。
当使用并行流时,Stream API会利用Fork/Join框架来并行处理数据。具体来说,Stream API会将大的数据集分割成多个小的数据块,然后利用Fork/Join框架的线程池来并行处理这些数据块。每个线程都会处理一个数据块,并将结果合并起来以得到最终的结果。
以下是一个简单的示例,展示了如何使用并行流和Fork/Join框架来计算一个大数组中所有元素的和:
import java.util.Arrays;
import java.util.concurrent.ForkJoinPool;
import java.util.stream.LongStream;
public class ForkJoinStreamExample {
public static void main(String[] args) {
// 创建一个包含大量元素的长整型数组
long[] numbers = LongStream.rangeClosed(1, 1000000000L).toArray();
// 默认使用Fork/Join框架的并行流来计算数组元素的和
long sum = Arrays.stream(numbers).parallel().sum();
// 打印结果
System.out.println("Sum of all elements: " + sum);
}
}
我们创建了一个包含大量元素的长整型数组,并使用Arrays.stream(numbers).parallel().sum()来计算数组中所有元素的和。这里,parallel()方法会将流转换为并行流,从而利用Fork/Join框架进行并行处理。sum()方法是一个归约操作,它会将流中的所有元素归约为一个单一的结果。
需要注意的是,虽然并行流可以显著提高处理大数据集的速度,但并不是所有情况下都应该使用它。如果数据集很小,或者每个元素的处理时间非常短,那么并行流可能会引入额外的开销,导致性能下降。因此,在使用并行流之前,最好先进行一些性能测试,以确定是否真正需要并行处理。
另外,值得注意的是,在Fork/Join框架中,任务的划分和合并是由框架自动处理的,而在Stream API中,开发者只需要指定要执行的操作,而不需要关心底层的并行处理细节。这使得使用Stream API进行并行处理变得更加简单和直观。
2. 再看自定义task任务的应用:
import java.util.concurrent.ForkJoinPool;
import java.util.concurrent.RecursiveTask;
// 继承 RecursiveTask,实现一个计算数组中元素和的任务
public class SumArrayTask extends RecursiveTask<Integer> {
// 数组
private final int[] array;
// 计算的起始索引
private final int start;
// 计算的结束索引
private final int end;
// 阈值,当子数组的长度小于此值时,直接计算结果而不再拆分
private static final int THRESHOLD = 10;
// 构造函数
public SumArrayTask(int[] array, int start, int end) {
this.array = array;
this.start = start;
this.end = end;
}
// 核心的计算方法
@Override
protected Integer compute() {
// 计算子数组的长度
int length = end - start;
// 如果子数组长度小于阈值,则直接计算该子数组的和
if (length <= THRESHOLD) {
int sum = 0;
for (int i = start; i < end; i++) {
sum += array[i];
}
return sum; // 直接返回结果
} else {
// 如果子数组长度大于阈值,则拆分任务
int middle = start + length / 2; // 计算中点
SumArrayTask leftTask = new SumArrayTask(array, start, middle); // 创建左半部分子任务
SumArrayTask rightTask = new SumArrayTask(array, middle, end); // 创建右半部分子任务
// 异步执行左半部分子任务(fork),并等待右半部分子任务的结果(compute)
leftTask.fork(); // fork 是不阻塞的,它会将任务提交到 ForkJoinPool 中去异步执行
int rightResult = rightTask.compute(); // compute 是阻塞的,它会等待任务完成并返回结果
// 等待左半部分子任务的结果,并与右半部分子任务的结果合并
int leftResult = leftTask.join(); // join 会阻塞,直到任务完成
return leftResult + rightResult; // 合并结果并返回
}
}
// 主函数,用于测试
public static void main(String[] args) {
int[] array = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16};
// 创建一个 ForkJoinPool,使用默认并行级别(通常等于处理器的核心数)
ForkJoinPool pool = new ForkJoinPool();
// 创建一个 SumArrayTask 任务来计算整个数组的和
SumArrayTask task = new SumArrayTask(array, 0, array.length);
// 提交任务到 ForkJoinPool 并获取结果
int sum = pool.invoke(task);
// 输出结果
System.out.println("The sum of the array elements is: " + sum);
}
}
在这个示例中,我们创建了一个 SumArrayTask 类,它继承了 RecursiveTask。SumArrayTask 的任务是计算一个整数数组中指定范围内的元素之和。如果数组的范围小于一个给定的阈值(THRESHOLD),则直接计算;否则,任务会在中点处被拆分为两个子任务,然后递归地执行这些子任务。
compute 方法是任务的核心,它根据数组的长度来决定是直接计算结果还是拆分任务。fork 方法用于异步提交左子任务到 ForkJoinPool,而 compute 方法会阻塞等待右子任务的结果。一旦两个子任务都完成,它们的结果会通过 join 方法合并,并返回给调用者。
在 main 方法中,我们创建了一个 ForkJoinPool 实例和一个 SumArrayTask 实例,然后使用 pool.invoke(task) 方法来执行任务并获取最终结果。这个结果被打印到控制台上。
五、ForkJoin框架的优点
- 自动并行化:通过简单地定义任务和递归地划分它们,开发者可以很容易地实现并行计算,而无需手动管理线程。
- 工作窃取:ForkJoinPool的工作窃取算法可以自动平衡负载,确保所有处理器核心都得到充分利用。
- 简单性:尽管其背后的原理可能很复杂,但使用ForkJoin框架的API相对简单,只需要实现少量的方法即可。
六、ForkJoin框架的局限性
- 递归划分:ForkJoin框架最适合可以递归划分的问题。对于不适合递归划分的问题,使用ForkJoin可能不是最佳选择。
- 任务开销:由于任务划分和结果合并的开销,对于非常小的任务,使用ForkJoin可能不如使用传统的单线程方法。
- 异常处理:在ForkJoin框架中处理异常可能比较复杂,因为异常需要在任务链中传播。
七、总结一下
Java中的ForkJoin框架是一个强大而灵活的并行计算工具。通过递归地划分任务和自动地平衡负载,它可以帮助开发者充分利用现代多核处理器的性能。然而,像所有工具一样,了解它的工作原理和局限性是使用它的关键。在适合的场景下,ForkJoin框架可以是一个强大的性能优化工具。






![[NOIP2011 提高组] 聪明的质监员](https://img-blog.csdnimg.cn/direct/d674fd8805504449be7207dd707f96ee.png)