引言

归并排序（Merge Sort) 是一种基于分治法的排序算法，它的基本思想是将原始数组划分成较小的数组，然后递归地对这些小数组进行排序，最后将排好序的小数组合并成一个整体有序的数组。
归并排序是一种稳定的排序算法，其时间复杂度为 O(n log n)，这使得它在大规模数据集上具有较好的性能。

基本应用:

1. 排序： 归并排序是一种高效的排序算法，其时间复杂度为 O(n log n)。它对于各种数据分布情况都有较好的性能，特别适用于链表结构。
2. 外部排序： 归并排序在外部排序中也很有用，因为它的排序过程不依赖于数据的分布。外部排序是处理大规模数据集无法一次加载到内存的情况下的一种排序方式。
3. 合并有序序列： 归并排序的合并过程可以轻松地用于合并两个有序序列。这在数据库操作中常被用来合并两个已排序的结果集。
4. 逆序数计算： 归并排序在计算逆序数（数组中的逆序对）时具有优势，因为在归并的过程中可以统计逆序对的数量。

1.归并排序的实现----c

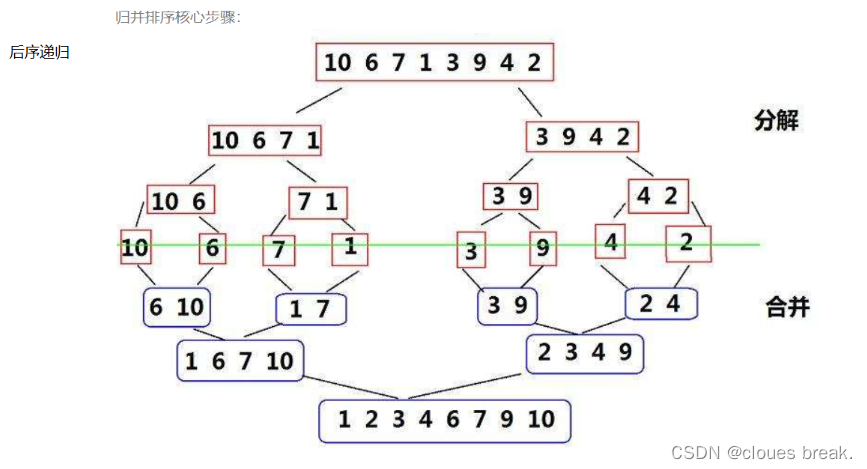
归并排序的思路是:本质是递归
将一个数组分成许多个小数组(直到最后单个数组有序,也就是只有一个元素),再将这些有序的小数组递归,由下往上返回

步骤:

1. 开辟动态数组,来复制之后有序的原数组
2. 将原数组划分成较小的数组,也就是单元素的数组
3. 将有序的数组拷贝,
4. 通过动态数组拷贝,返回的有序小数组集成为有序原始数组

//归并排序
void _MergeSort(int* a, int begin, int end, int* tmp)
{
	//若一个区间只有一个元素，返回
	if (begin >= end)
		return;
	//若区间为不有序
	//记录中间坐标
	int mid = (begin + end) / 2;
	_MergeSort(a, 0, mid, tmp);
	_MergeSort(a, mid+1, end, tmp);
	//将有序的小区间集成为有序大区间
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
	while (begin1<=end1&& begin2<=end2)
	{
		//俩数组比较
		if (a[begin1] <= a[begin2])
			tmp[i++] = a[begin1++];
		else
			tmp[i++] = a[begin2++];
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	//注意拷贝的时候，数组的起始位置与拷贝空间大小
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc ");
		return;
	}
	//递归拷贝，分组
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}

2.归并排序的复杂度分析

时间复杂度

时间复杂度是O(n log n)

分为俩部分:
合并
每一层的合并操作的总时间复杂度是 O(n)
递归
递归的算法类似于二叉树后序遍历的时间复杂度,也就是递归深度,log n

空间复杂度

空间复杂度是 O(log n)

归并排序的空间复杂度相对较高，主要取决于递归调用的栈空间和临时数组的存储空间。
在最坏情况下，递归树的深度达到 log n ,因此空间复杂度是 O(log n)。此外，合并过程需要额外的 O(n) 空间来存储临时数组。