博主介绍:✌专研于前后端领域优质创作者、本质互联网精神开源贡献答疑解惑、坚持优质作品共享、掘金/腾讯云/阿里云等平台优质作者、擅长前后端项目开发和毕业项目实战,深受全网粉丝喜爱与支持✌有需要可以联系作者我哦!
👇🏻 精彩专栏推荐订阅👇🏻 不然下次找不到哟
目录
一、什么是贪心算法
贪心算法的一般流程如下:
二、常见应用算法
Prim算法:贪心算法的一种常见应用是Prim算法。Prim算法的基本思想是从一个初始顶点开始,每次选择一条边,将一个新的顶点纳入生成树中,直到所有的顶点都被纳入生成树。
活动选择问题(Activity Selection Problem):
三、小结:
最后欢迎三连点赞、关注、收藏哦!
一、什么是贪心算法
贪心算法(Greedy Algorithm)是一种在每一步选择中都采取当前状态下最优解的策略,希望通过一系列局部最优的选择最终达到全局最优。贪心算法通常用于优化问题,其中在每个阶段都做出局部最优的选择,希望通过这种方式达到全局最优解。
贪心算法的主要特点是它对解的选择没有显式的规定,而是通过一系列的局部选择来达到整体最优。每一步都选择当前状态下的最优解,而不考虑未来的影响。
贪心算法的一般流程如下:
- 问题建模: 将问题抽象成一系列的局部最优选择。
- 选择策略: 确定每一步的选择策略,即如何在当前状态下做出最优的选择。
- 解决问题: 通过贪心策略逐步解决问题,直到达到全局最优解或者近似最优解。
虽然贪心算法在一些问题中非常有效,但并不是所有问题都适合使用贪心算法。在某些情况下,贪心算法可能无法得到全局最优解,因为它不进行回溯。因此,在使用贪心算法时,需要仔细分析问题的特性,确保贪心策略能够达到预期的最优解。典型的贪心算法应用包括最小生成树、单源最短路径、任务调度等。
二、常见应用算法
Prim算法:贪心算法的一种常见应用是Prim算法。Prim算法的基本思想是从一个初始顶点开始,每次选择一条边,将一个新的顶点纳入生成树中,直到所有的顶点都被纳入生成树。
#include <iostream>
#include <climits>
using namespace std;
#define V 5 // 顶点数
int minKey(int key[], bool mstSet[]) {
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++) {
if (!mstSet[v] && key[v] < min) {
min = key[v];
min_index = v;
}
}
return min_index;
}
void printMST(int parent[], int graph[V][V]) {
cout << "Minimum Spanning Tree (Prim):" << endl;
for (int i = 1; i < V; i++)
cout << "Edge: " << parent[i] << " - " << i << " Weight: " << graph[i][parent[i]] << endl;
}
void primMST(int graph[V][V]) {
int parent[V];
int key[V];
bool mstSet[V];
// 初始化所有键值为无穷大,都未包含在生成树中
for (int i = 0; i < V; i++) {
key[i] = INT_MAX;
mstSet[i] = false;
}
// 选择第一个顶点作为起始点
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++) {
if (graph[u][v] && !mstSet[v] && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
printMST(parent, graph);
}
int main() {
int graph[V][V] = { {0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0} };
primMST(graph);
return 0;
}
执行结果:
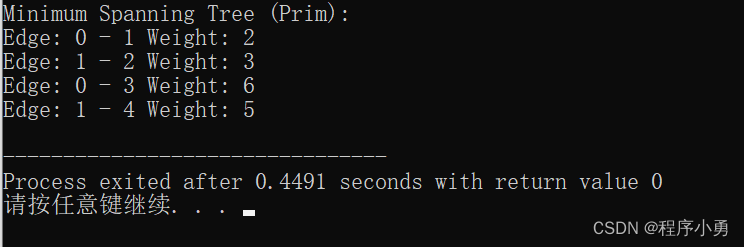
活动选择问题(Activity Selection Problem):
假设有一个教室,需要安排一系列活动,每个活动都有一个开始时间和结束时间。活动之间不能重叠,即同一时间教室只能进行一个活动。目标是选择尽可能多的活动,使得它们不会相互冲突,即在给定时间内进行尽可能多的非重叠活动。
C++代码:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
// 首先声明一个活动结构体,包含活动开始时间和结束时间两个变量
struct Activity {
int start, finish;
};
// 按照活动结束时间升序排序的比较函数
bool compare(Activity a, Activity b) {
return (a.finish < b.finish);
}
// 贪心算法解决活动选择问题
void printMaxActivities(Activity activities[], int n) {
// 按照结束时间升序排序
sort(activities, activities + n, compare);
cout << "Selected Activities:\n";
// 第一个活动总是被选中
int i = 0;
cout << "(" << activities[i].start << ", " << activities[i].finish << "), ";
// 遍历剩余活动
for (int j = 1; j < n; j++) {
// 如果当前活动的开始时间大于等于上一个选中活动的结束时间,选择当前活动
if (activities[j].start >= activities[i].finish) {
cout << "(" << activities[j].start << ", " << activities[j].finish << "), ";
i = j;
}
}
}
int main() {
// 示例活动数据(活动开始实践和结束时间)
Activity activities[] = {{1, 2}, {3, 4}, {0, 6}, {5, 7}, {8, 9}, {5, 9}};
int n = sizeof(activities) / sizeof(activities[0]);
// 调用贪心算法解决活动选择问题
printMaxActivities(activities, n);
return 0;
}
活动按照结束时间升序排序,然后使用贪心算法选择尽可能多的不重叠活动。这个算法的时间复杂度为O(n log n),其中n是活动的数量。
执行结果:
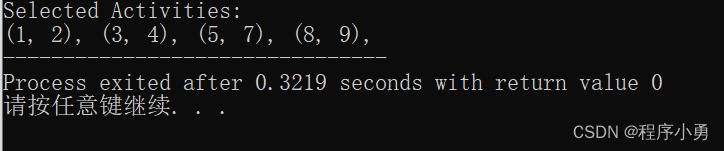
三、小结:
1. 基本思想:
- 贪心算法是一种在每一步选择中都采取当前状态下最优解的策略,希望通过一系列局部最优的选择达到全局最优。
- 贪心策略通常不进行回溯,一旦做出选择就不再改变。
2. 适用条件:
- 问题具有最优子结构性质:问题的最优解可以通过子问题的最优解推导得到。
- 贪心选择性质:每一步的选择都是当前状态下的最优解,即局部最优。
3. 过程步骤:
- 建模: 将问题抽象成一系列局部最优的选择。
- 选择策略: 确定每一步的选择策略,即如何在当前状态下做出最优的选择。
- 解决问题: 通过贪心策略逐步解决问题,直到达到全局最优解或者近似最优解。
4. 优缺点:
- 优点: 算法简单、高效,适用于一些问题,尤其是最优子结构和贪心选择性质明显的情况。
- 缺点: 不适用于所有问题,可能得不到全局最优解,只能得到局部最优解或者近似最优解。
5. 注意事项:
- 贪心算法的适用性需要仔细分析问题的性质,确保贪心策略能够达到预期的最优解。
- 在一些问题中,贪心算法可以作为求解问题的一部分,而不是整个问题的解决方案。
最后欢迎三连点赞、关注、收藏哦!