引言

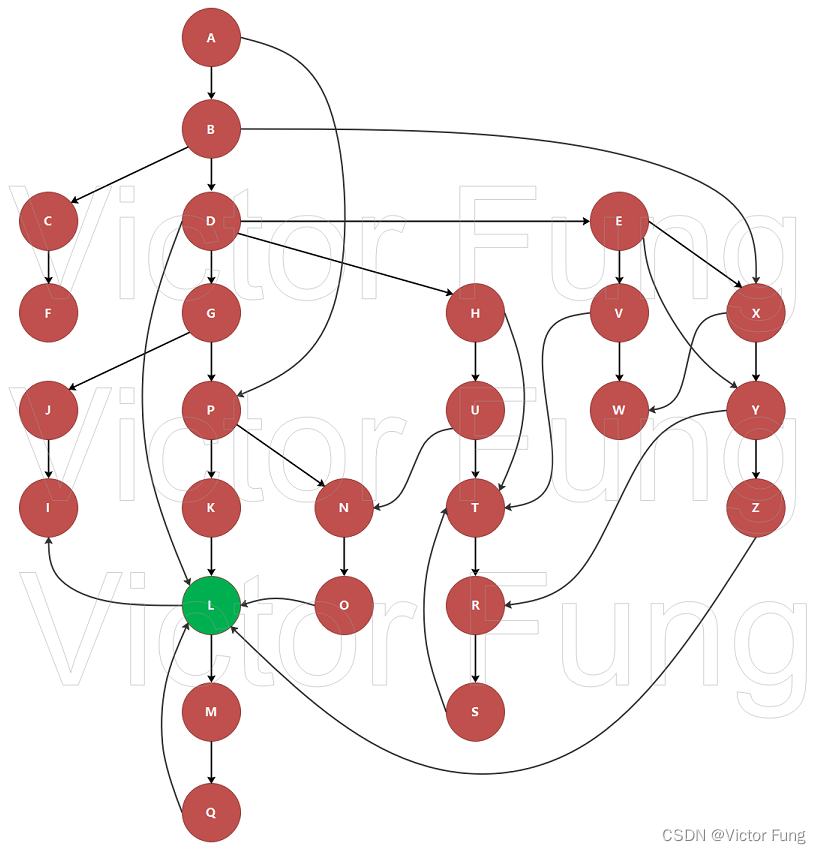
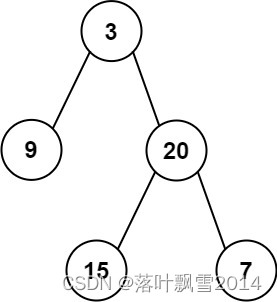
如上一个带有起始入口点的有向图为例，从A到Q的必经结点有A、L、M、Q，我们称其为Q的支配点，其中M为Q的最近支配点。我们将每个结点的最近支配结点指向自己，形成一颗如下图的树。该树就是图的支配树。

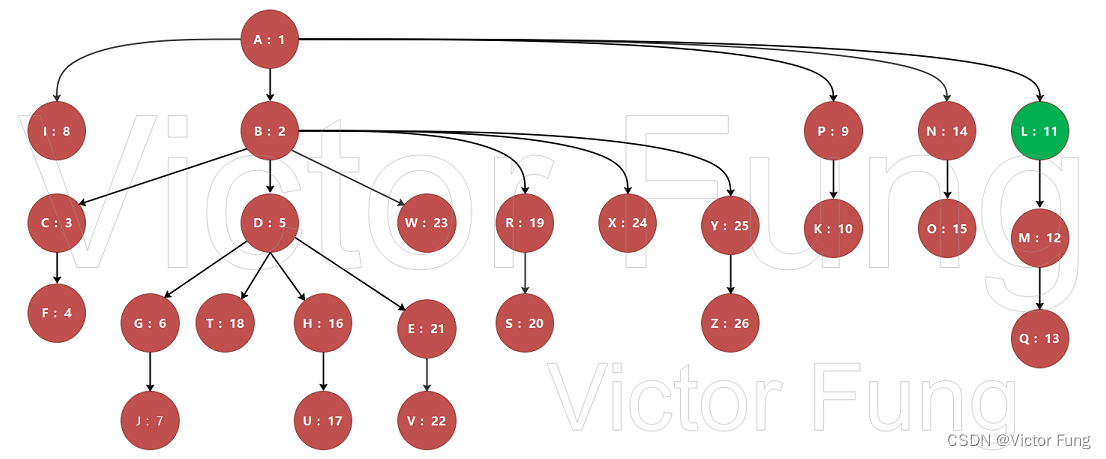
在编译器中，支配树作用显著。例如，它可以辅助我们识别函数中的循环等功能。本文将将讨论如何从一个图构建支配树？

1 分析有向图

首先，我们从图的起始入口点A执行深度优先搜索，并在搜索过程中依次对结点进行从小到大标记序号(即DFS序号，简称dfn)。最终，形成如下图：

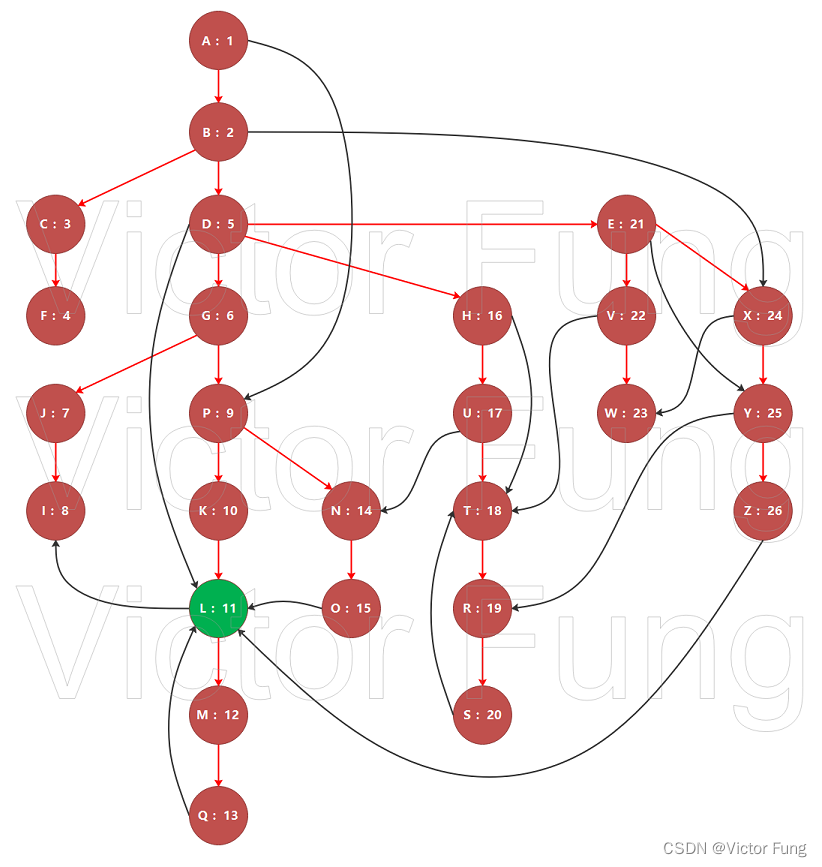
注：图中红色链路，为DFS树的边。

对图中结点进行观察，发现如下一些特性：

• 图中，偏左枝兄弟上的结点永远不可能指向偏右枝上的任意结点。如果可以，那么根据DFS搜索规则，最终形成的搜索树就会发生变化。
• 图中，任意结点的必经结点必定在A到该节点的DFS搜索路径上。也就是说任意结点的必经结点的dfn必小于等于该节点的dfn。

2 构建支配树

构建支配树的算法，可以总结为如下几步：

1. 首先，求出所有结点的最小半支配点；
2. 然后，通过最小半支配点求出每个结点的最近支配点；
3. 最后，依靠最近支配点串成支配树。

注1：点p的半支配点q满足: dfn[q] <= dfn[p] 且 存在一条q到p的路径上的任意结点(不包括q、p)的dfn都大于p的dfn。特别地，若q的dfn小于p的dfn，且q直接指向p，那么q也是p的半支配点；同时，结点自身也是自己的半支配点；
注2：点p的最小半支配点就是p的所有半支配点中dfn最小的结点。

2.1 求最小半支配点

我们以结点L为例，L共有五个前驱结点，按dfn分为两组：

• 第一组是dfn小于L的结点，有两个：D和K；
• 第二组是dfn大于L的结点，有三个：O、Z、Q；

求最小支配结点算法如下：

1. 首先，对于第一组的两个结点，其dfn满足半支配点的定义，所以它们直接加入到L的半支配点列表中；
2. 对于第二组的每个结点：采用递归思想求其半支配点。对于dfn小于或等于L的dfn的半支配点，将其加入到L的半支配点列表中；对于dfn大于L的dfn的半支配点，继续求这些半支配点的半支配点；以此类推。。。采用层层向上，直到求出的所有支配点的dfn小于或等于L的dfn(即11)并加入到L的半支配点列表后终止递归。
   最后，O往上求得半支配点是P、D；Z往上求得半支配点是B、D；Q往上求得半支配点是L自身。
3. 最后在L的半支配点列表中，选dfn最小的结点作为L的最小半支配点（即B）。

注：实际算法实现中，可以将L的最小半支配点初始化为自身； 每次迭代L的前驱结点时，按照上述方法求得其半支配点后，与当前L的最小半支配点比较dfn大小，发现比其小，就将其更新。这样省略最后在所有半支配点中迭代dfn最小的半支配点。

2.2 求最近支配点

一般，最小半支配点极可能就是最近支配点。但是，也会有特殊情况，例如L的最小半支配点B到L的DFS路径上有一条A->P的路径对B旁支了；也就是说这时B，并不是L的支配点。

通过最小半支配点求最近支配点算法如下：

1. 首先，将最小半支配点的dfn初始化为迭代终止值；

2. 从L开始沿着DFS搜索路径反向往上遍历，每遍历一个结点：
   若迭代结点的dfn值等于迭代终止值，则终止迭代。
   反之，又若该结点的最小半支配点的dfn小于迭代终止值，则将该结点的最小半支配点的dfn更新为迭代终止值；

3. 最后的迭代终止结点就是L的最近半支配点。

注：按照上述算法，最后求得L的最近支配点为A。