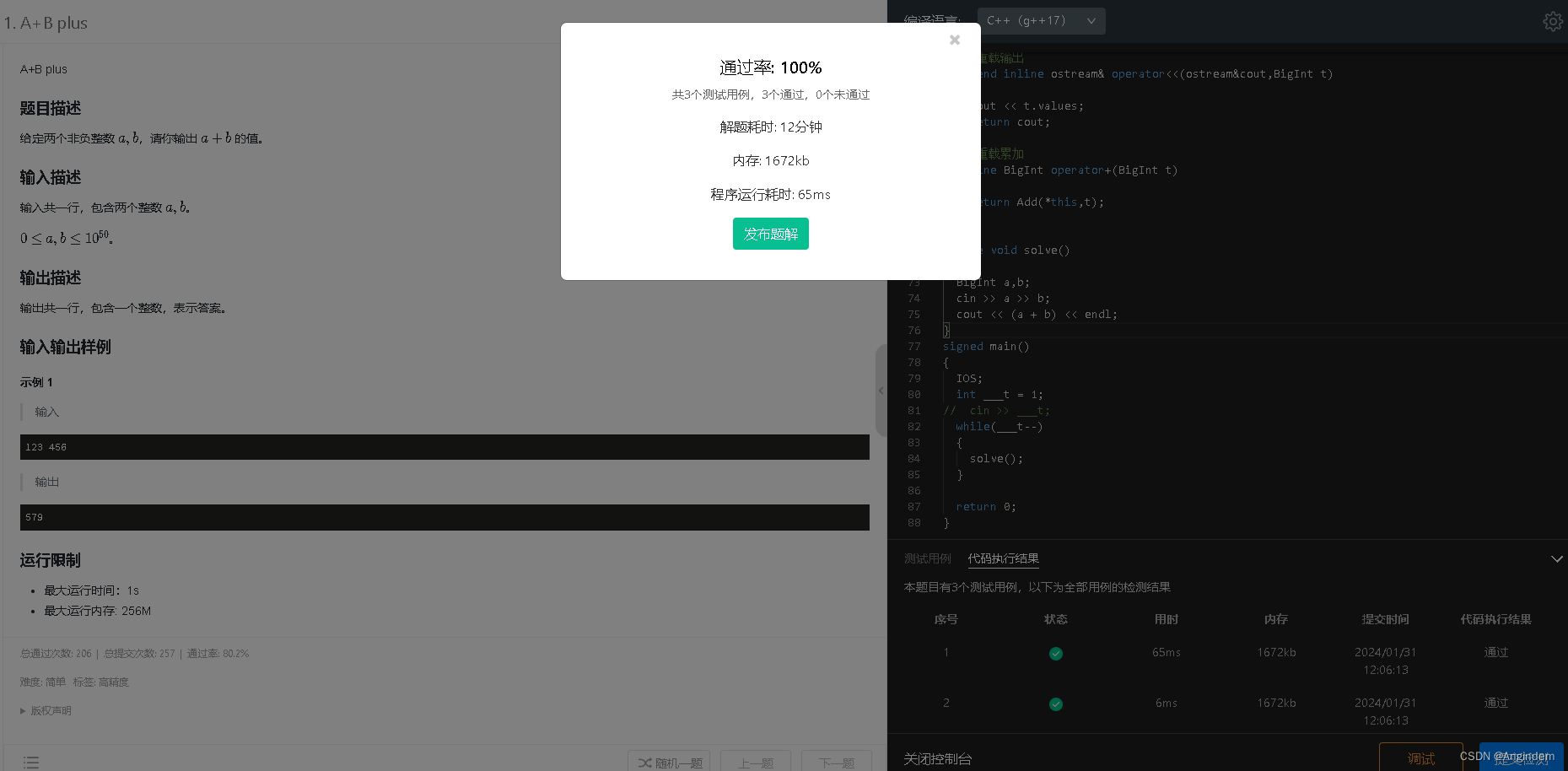
本题链接：用户登录

题目：

样例：

123 456

模板结构体：

struct BigInt
{
	string values;
	inline BigInt Add(const BigInt &ta,const BigInt &tb)
	{
		BigInt ans;
		ans.values = "";
		string sa = ta.values;
		string sb = tb.values;
		int alen = sa.size();
		int blen = sb.size();
		vector<int>a,b,c;
		for(int i = alen - 1;~i;--i) a.emplace_back(sa[i] - '0');
		for(int i = blen - 1;~i;--i) b.emplace_back(sb[i] - '0');
		int t = 0;
		for(int i = 0;i < alen || i < blen;++i)
		{
			if(i < alen) t += a[i];
			if(i < blen) t += b[i];
			c.emplace_back(t % 10);
			t /= 10;
		}
		if(t) c.emplace_back(1);
		int clen = c.size();
		for(int i = clen - 1;~i;--i) ans.values += char(c[i] + '0');
		return ans;
	}
	friend inline istream& operator>>(istream&cin,BigInt& t)
	{
		cin >> t.values;
		return cin;
	}
	friend inline ostream& operator<<(ostream&cout,BigInt t)
	{
		cout << t.values;
		return cout;
	}
	inline BigInt operator+(BigInt t)
	{
		return Add(*this,t);	
	}
};

思路：

        大整数，高精度，运算原理跟我们小学进行的笔算原理一样的，模拟一遍即可。

代码详解如下：

#include <iostream>
#include <cstring>
#include <vector>
#define endl '\n'
#define int long long
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;

struct BigInt
{
	string values;
	inline BigInt Add(const BigInt &ta,const BigInt &tb)
	{
		BigInt ans;			// 建立返回值
		ans.values = "";	// 返回值初始化
		
		string sa = ta.values;	// 取出整数 a 的值
		string sb = tb.values;	// 取出整数 b 的值
		
		int alen = sa.size();	// 获取整数 a 的位数
		int blen = sb.size();	// 获取整数 b 的位数
		
		vector<int>a,b,c;	// 定义存储计算过程的数组
		
		// 将字符串反向转化为数组方便运算。
		// 由于string是由高位到低位的存储，所以我们反向，方便运算个位等低位的运算
		for(int i = alen - 1;~i;--i) a.emplace_back(sa[i] - '0');
		for(int i = blen - 1;~i;--i) b.emplace_back(sb[i] - '0');
		
		int t = 0;	// 临时变量 t 存储同一位数上的累加结果
		// 开始累加过程
		for(int i = 0;i < alen || i < blen;++i)
		{
			// 如果对应的位数存在，那么开始累加
			if(i < alen) t += a[i];
			if(i < blen) t += b[i];
			
			// 取出当前位的累加结果
			c.emplace_back(t % 10);
			
			// 除掉当前位，若可以进位则进位
			t /= 10;
		}
		// 如果计算结果最后还有进位，我们就开始进位
		if(t) c.emplace_back(1);
		
		int clen = c.size();	// 获取最终计算结果位数
		// 颠倒重新由高位存储低位
		for(int i = clen - 1;~i;--i) ans.values += char(c[i] + '0');
		return ans;	// 返回结果
	}
	
	// 重载输入
	friend inline istream& operator>>(istream&cin,BigInt& t)
	{
		cin >> t.values;
		return cin;
	}
	// 重载输出
	friend inline ostream& operator<<(ostream&cout,BigInt t)
	{
		cout << t.values;
		return cout;
	}
	// 重载累加
	inline BigInt operator+(BigInt t)
	{
		return Add(*this,t);	
	}
};
inline void solve()
{
	BigInt a,b;
	cin >> a >> b;
	cout << (a + b) << endl;
}
signed main()
{
	IOS;
	int ___t = 1;
//	cin >> ___t;
	while(___t--)
	{
		solve();
	}
	
	return 0;
}

最后提交：