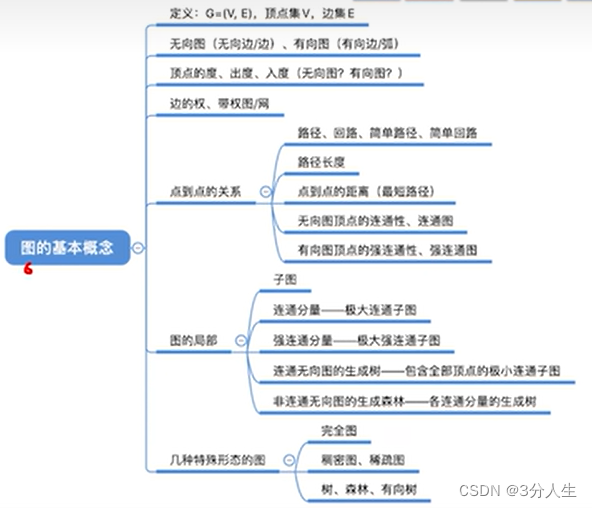
图的基本概念和术语

图的定义：图是由顶点的有穷非空集合和顶点之间的边的集合组成的，G表示，V是图G中顶点的集合，E是图G中边的集合

无向图：任意两点的边都是无向边组成的图（无向边：（A,B)表示点A能到点B，点B也能到点A）

有向图：任意两点的弧都是有向边组成的图（有向边：<A,B>表示点A能到点B，点B不能到点A（B为弧头，A为弧尾）

边较少的图叫稀疏图，反之叫稠密图

权，网：图的边或弧相关的数叫权，这种带权的图通常叫做网

顶点的度：无向图中顶点的度表示和顶点相关联的的边的数目（记TD)；有向图中分为入度和出度

 入度为顶点为弧头有关联的弧，出度为顶点为弧尾有关联的弧

路径长度：路径长度是路径上边或弧的数目

回路，环：第一个顶点和最后一个顶点相同的路径称为回路或环

连通图：图中任意两点都是连接的（有路径），有向图中称为强连通图

无向图中联通n个顶点和n-1条边叫生成树，有向图中一顶点入度为0其余顶点入度为1的叫有向树。

 

 

 图的储存结构

邻接矩阵

图的邻接矩阵采用顺序存储结构，用一个一维数组储存顶点的信息，一个二维数组储存图中边或弧的的信息

优点：便于理解，适合稠密图，O(1)判断两点是否有边，删除边比较方便

缺点：遇到边较少的图，浪费大量空间，图的建立，dfs，bfs遍历时间复杂度较高为O(N^2)，删除点不方便

 邻接表

邻接表采用顺序+链式存储结构，一个一维结构体数组（数组大小为结点数量），结构体数组的存储元素构成单链表，每一个单链表链接与该结点相连的点

 优点：根据需求分配空间，浪费的空间较少，适合稀疏图

 缺点：删除边或点比较麻烦，对于有向图不利于求某个点出度的数量

 

 图的遍历

广度优先遍历和深度优先遍历，对于邻接矩阵和邻接表的时间复杂度都为平方阶和线性阶

 所以对于有关于图的遍历问题一般采用邻接表储存图，时间开销更小

图中如果不是联通图，存在一次遍历不能遍历全部的点，一般用数组标记判断点是否遍历

 模板题 洛谷 P5318 查找文献

本题考察图的深度和广度

题目描述

小 K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个（也有可能没有）参考文献的链接指向别的博客文章。小 K 求知欲旺盛，如果他看了某篇文章，那么他一定会去看这篇文章的参考文献（如果他之前已经看过这篇参考文献的话就不用再看它了）。

假设洛谷博客里面一共有n(n≤10^5) 篇文章（编号为 1 到 n）以及 m(m≤10^6) 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章，请帮助小 K 设计一种方法，使小 K 可以不重复、不遗漏的看完所有他能看到的文章。

这边是已经整理好的参考文献关系图，其中，文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。

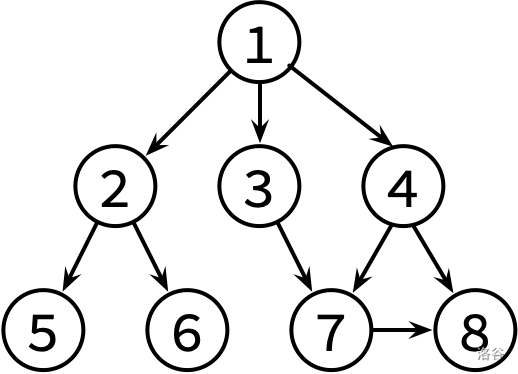
请对这个图分别进行 DFS 和 BFS，并输出遍历结果。如果有很多篇文章可以参阅，请先看编号较小的那篇(因此你可能需要先排序)。

输入格式

共 m+1 行，第 1 行为 2 个数，n 和 m，分别表示一共有 n(n≤10^5) 篇文章（编号为 1 到 n）以及m(m≤10^6) 条参考文献引用关系。

接下来 m 行，每行有两个整数 X,Y 表示文章 X 有参考文献 Y。

输出格式

共 2 行。 第一行为 DFS 遍历结果，第二行为 BFS 遍历结果。

输入输出样例

输入 #1

8 9
1 2
1 3
1 4
2 5
2 6
3 7
4 7
4 8
7 8

输出 #1

1 2 5 6 3 7 8 4 
1 2 3 4 5 6 7 8 

 看题发现本题的n的范围10^5用邻接矩阵不仅空间存不下，遍历也浪费时间，所以采用邻接表

这题不需要考虑是否为连通图，题目的数据，若是存在一个点与1号点没有联系则不需要输出这个点

思路

我们知道邻接表遍历结果不唯一的，而题目要求请先看编号较小的那篇(因此你可能需要先排序)，链表不好进行排序，我们可以先对输入的m个x和y进行排序，因为对于邻接表一般采用头插法（先插入的点在链表的最后），按照y的比较进行降序排列，这样可以保证每一个单链表都是升序。

AC代码

#include<stdio.h>
#include<stdlib.h>
struct nb {
	int data;
    struct nb* p;
}a[100010];//邻接表
struct mm {
	int l, r;
}mr[1000010], b[1000010];//b为归并辅助数组
void guibin(int x, int y)//归并排序不多说
{
    if (x >= y) return;
    long long mid = (x + y) / 2, i, j;
    guibin(x, mid);
    guibin(mid + 1, y);
    int cnt = 0;
    for (i = x, j = mid + 1; i <= mid && j <= y;)
    {
        if (mr[i].r >= mr[j].r)
            b[++cnt] = mr[i++];
        else
            b[++cnt] = mr[j++];
    }
    while (i <= mid)
        b[++cnt] = mr[i++];
    while (j <= y)
        b[++cnt] = mr[j++];
    for (i = 1; i <= cnt; i++)
        mr[x + i - 1] = b[i];
}
int book[100010], book1[100010] = { 0 };//标记数组
void dfs(int  x)
{
    struct nb* gg;
    book[x] = 1;//第一次访问标记为1
    printf("%d ", x);//打印结果
    gg = a[x].p;
    while (gg)
    {
        if (book[gg->data] == 0)//第一次访问dfs搜索
            dfs(gg->data);
        gg = gg->p;
    }
}
void bfs(int x)
{
    int link[100010];
    int hard = 1, tail = 2;
    link[1] = x; book1[x] = 1;
    while (hard < tail)
    {
        printf("%d ", link[hard]);
        struct nb* f = a[link[hard]].p;
        while (f != NULL)
        {
            if (book1[f->data] == 0)
            {
                link[tail++] = f->data;
                book1[f->data] = 1;
            }
            f = f->p;
        }
        hard++;
    }
}
int main()
{
	int n, m, i, j;
    struct nb* q, * t, * s;
	scanf("%d %d", &n, &m);
	for (i = 1; i <= m; i++)//输入m个x,y
		scanf("%d %d", &mr[i].l, &mr[i].r);
    for (i = 1; i <= n; i++)
        a[i].p = NULL;
    guibin(1, m);//降序排序
    for (i = 1; i <= m; i++)//邻接表的建立
    {
        q = (struct nb*)malloc(sizeof(struct nb));
        q->data = mr[i].r; q->p = a[mr[i].l].p;
        a[mr[i].l].p = q;
    }
    dfs(1);//dfs搜索
    printf("\n");
    bfs(1);//bfs搜索
    for (i = 1; i <= n; i++)//清空邻接表链表，避免内存泄露
    {
        s = a[i].p;
        while (s != NULL)
        {
            t = s;
            s = s->p;
            free(t);
        }
    }
	return 0;
}