【机器学习300问】21、什么是激活函数？常见激活函数都有哪些？

news2024/9/21 16:34:20

在我写的上一篇文章中介绍了感知机（单个神经元）的构成，其中就谈到了神经元会计算传送过来的信号的总和，只有当这个总和超过了某个界限值时，才会输出值。这也称为“神经元被激活”。如果想对神经网络是什么有更多了解的小伙伴可以去看看我上一篇文章，链接我发在下面啦！
【机器学习300问】20、什么是神经网络？和深度学习什么关系？http://t.csdnimg.cn/47Sgq

承接上文中谈到的“神经元被激活”，我们介绍一个神经网络中非常基础的知识点——激活函数。

一、什么是激活函数？

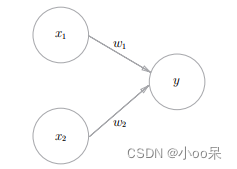
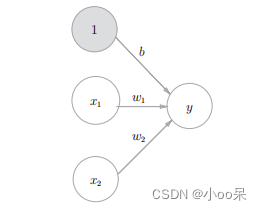
图中是一个神经元，它有两个输入 $(x_1,x_2)$ 分别有着两个权重 $(w_1,w_2)$ ，如果写成数学公式的话就是下面这样的形式：

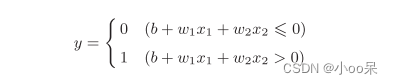
b是被称为偏置的参数，用于控制神经元被激活的容易程度；而w和是表示各个信号的权重的参数，用于控制各个信号的重要性。这里假设被“激活”输出1，“未激活”输出0，如果简化一下公式将其写成：

$y=h(b+w_1x_1+w_2x_2)$

输入的信号会经过h函数的处理，只有在满足条件的时候才能输出y。那么不同的h函数就对应着不同的“激活”条件，这个h函数就是激活函数。

在这里我进一步处理一下公式，令 $a=b+w_1x_1+w_2x_2$ ，那么最终激活函数就可以写成 $y=h(a)$ 。这里解释一下为什么这么令，a是单词“激活值”activation，因为上一层的激活值就是下一层的输入值，而这个激活值就是通过公式 $b+w_1x_1+w_2x_2$ 计算出来的。

二、常见的激活函数

（1）阶跃函数

在上面的例子里，我们自然会想到，大于0就“激活”输出，小于等于0就“未激活”不输出（换言之输出值为0），那么按照这样的规则进行激活，写成公式的形式：

$h(a)=\left\{\begin{matrix} 0 &(a< 0) \\ 1 &(a\geqslant 0) \end{matrix}\right.$

画出他的图像：

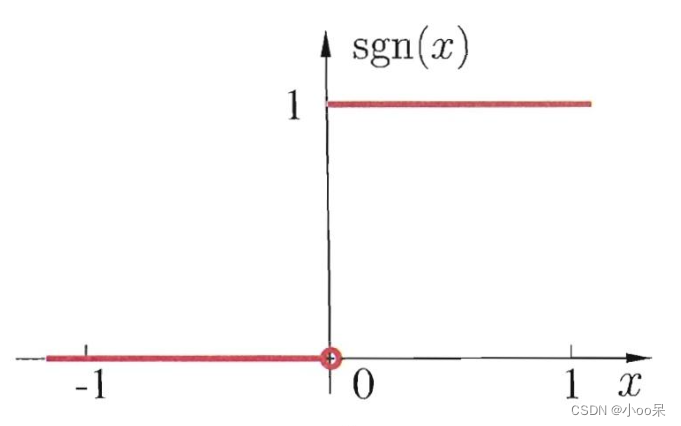
虽然阶跃函数非常好理解很直观，但在神经网络的激活函数选择中，一般不会使用阶跃函数作为激活函数。因为它有如下几个不足：

不连续性：阶跃函数在阈值处不连续，导数在阈值处不存在，这在反向传播过程中会导致梯度消失，无法有效地更新权重。
导致饱和问题：在输出层，一旦神经元的输入越过阈值，无论输入如何变化，输出始终保持不变，不利于模型的学习和优化。
缺乏平滑性：由于非平滑性，模型很难通过梯度下降法等优化算法来找到合适的权重，这在现代深度学习优化中是一个严重的限制。

（2）Sigmoid函数

神经网络中常用的一个激活函数，必须掌握。Sigmoid函数的输出在(0, 1)之间，可用于处理二分类问题，可以将连续数转化为概率。它的数学表达式如下：

$h(a) = \frac{1}{1 + e^{-a}}$

画出他的图像：

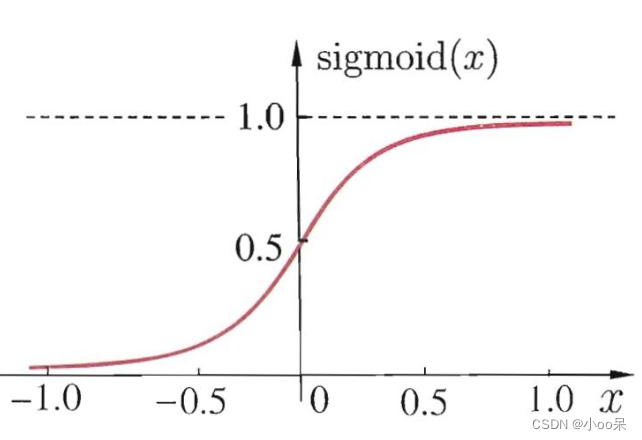
优点：S型函数，输出值在0-1之间，具有良好的连续性和可微性。
缺点：可能产生梯度饱和现象，即网络无法从数据中学习；对于神经网络层次较深的情况，容易出现梯度消失问题。

【注】梯度消失：在这里不展开细讲，简单理解就是在当网络层数增加时，梯度值越来越小，直到几乎为零，这就是所谓的梯度消失现象。如果想深入学习梯度相关知识，可以看看我之前写的文章

【机器学习300问】9、梯度下降是用来干嘛的？

（3）Tanh函数

它还有个名字叫做双曲正切函数，输出范围在(0, 1)之间，常用于二元逻辑回归和早期的多层感知器（MLP）的隐藏层，现在较少在现代深度学习中作为隐层激活函数。数学表达式为：

$h(a) = \frac{e^{a} - e^{-a}}{e^{a} + e^{-a}}$

画出他的图像：

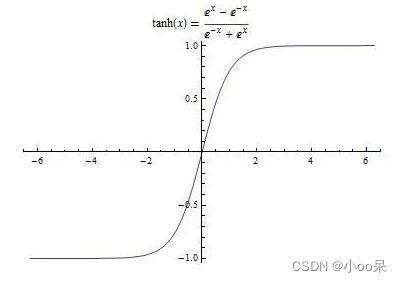
优点：比sigmoid函数的数据压缩范围要大，在反向传播中不会那么容易饱和
缺点：依然存在梯度消失问题，当输入很大或很小时，导数非常接近于0，这会减慢训练速度，训练起来也相较复杂

（4）ReLU函数

Rectified Linear Units可以翻译成线性整流函数，但一般就直接用缩写称呼它。当输入大于0时输出等于输入本身，小于等于0时输出恒为0。正因为ReLU函数将负数转化为0，保留正数不变，所以解决了梯度消失和梯度爆炸的问题。数学表达式如下：

$h(a) = max(0, a)$

或

$h(a)=\left\{\begin{matrix} a & (a>0)\\ 0 & (a\leqslant 0) \end{matrix}\right.$

画出他的图像：

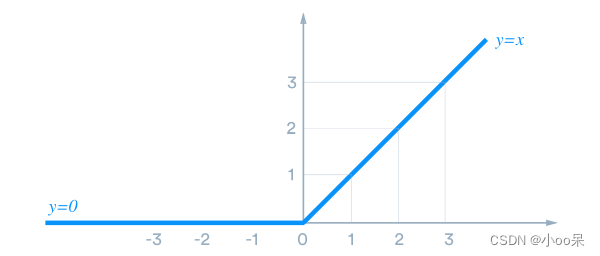
优点：训练速度快，避免了梯度消失问题，并能加快收敛速度
缺点：ReLU在负值部分完全不激活，一旦输入在训练过程中到达零或者负值，那么该神经元在任意数据点的梯度都是0,那么这个神经元将会不再对任何数据敏感，也就是说这个神经元已经死去了

【注】梯度爆炸：和梯度消失一样，是深度神经网络训练中遇到的常见问题，表现正好相反。通常发生在层数较多的情况下，在反向传播过程中，当错误从网络的最后一层向前传播时，梯度会逐渐积累，最终在最早的层变得非常大。

（5）Softmax函数

它将一系列数值转换为概率分布的形式，所有输出的概率总和为1，在多分类问题中特别有用，尤其是输出层。它的数学公式如下：

$h(a_{j})=\frac{e^{a_{j}}}{\sum_{i}^{n}e^{a_{i}}}$

看上去很复杂，听我给你解释一下。分子是输入信号aj的指数函数，分母是所有输入信号的指数函数的和。

$a_{j}$	是第 j 个神经元的输入
$a_{i}$	某一个神经元的输入
$\sum_{i}^{n}e^{a_{i}}$	所有输入的指数函数之和
$n$	类别的总数（一共有多少个类别）