前言

打满 2个小时30分钟 基本都在做题 体验非常好
传送门 : https://codeforces.com/gym/103118

G. Grade Point Average ( 难度有先后)

题意 :

让你求$sum/n$并且需要输出保留的后面几位

思路 :
因为这里并没有考虑进位输出,所以不考虑使用函数输出(当然我也不会)

自己简单模拟一下除法的过程,就会发现每次我们都需要拿出上一个除出来的余数当作现在的除数

code :

int n,k;
void solve(){
	cin>>n>>k;
	int sum =  0 ;
	
	Fup(i,1,n){
		int x;cin>>x;
		sum+=x;
	}
	
	cout<<sum/n<<".";
	
	int rm = 0 ;
	Fup(i,1,k){
		rm = sum%n;
		rm *= 10;
		sum = rm;
		
		rm /= n;
		cout<<rm;
	}
}

M. Matrix Problem

题意 :

给你一个已知数组$C$,然你构造两个数组$A,B$。这两个数组需要满足只有在$C$为1的时候,$AB$才可以为1,否则的话不能相同。

**另外构造出来的$A,B$**对于每一个$1$都需要连通

思路 :
样例答案很明显了
我们考虑构造$双E$的形式,这样子对于A数组和B数组既可以保证连通,同时又可以保证不为1的时候我们不相同

题目中双E的形式

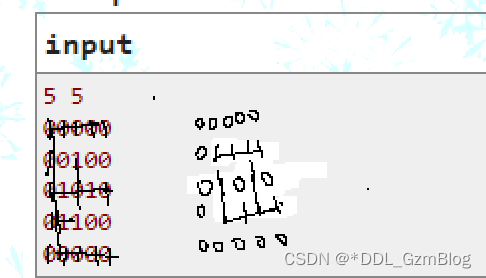
code :

char a[N][N],b[N][N],c[N][N];

void solve(){
	int n,m;cin>>n>>m;
	
	Fup(i,1,n){
		Fup(j,1,m){
			cin>>c[i][j];
			a[i][j] = c[i][j];
			b[i][j] = c[i][j];
		}
	}
	
	Fup(i,1,n){
		if(i%2 == 1){
			Fup(j,1,m-1) a[i][j] = '1';
		}else a[i][1] = '1';
	}
	
	Fup(i,1,n){
		if(i%2 != 1){
			Fup(j,2,m) b[i][j] = '1';
		}else b[i][m] = '1';
	}
	
	Fup(i,1,n){
		Fup(j,1,m){
			cout<<a[i][j];
		}
		cout<<endl;
	}
	
	Fup(i,1,n){
		Fup(j,1,m){
			cout<<b[i][j];
		}
		cout<<endl;
	}
	

}

H. Adventurer’s Guild

题意 :
有$n$个怪物,每个怪物需要对主角进行消耗$h[i],s[i]$ , 如果选择消灭这个怪物那么就可以获取$w[i]$的硬币

对于主角有$H,S$。询问如何选择才可以获得最多的硬币

这题的需要注意的是 如果$S$不够,那么我们可以选择从$H$借

思路 :
因为过的人比较多,所以一开始没选择$dp$方向。而是考虑了一下反悔贪心。不过很显然的这个每次的增量并不是固定的,所以反悔贪心不作考虑。

同时又因为很明显的两个状态$H,S$因此我们考虑二维费用背包

二维费用背包 : https://www.acwing.com/problem/content/8/
二维费用背包概述 : https://www.acwing.com/activity/content/code/content/1902854/

但是对于普通的二维费用背包我们并没有考虑可以有 借,即题目中$S可以向H借$ 这种说法

简单思考一下 , 因为最后借的时候,状态转移还是转移到一个状态即$f[h][0]$所以我们还是可以使用$dp$

状态表示 :
$f[H][S]$ 最大血量$H$ 最大$S$的情况下的最多硬币
状态转移 :
$f[H][S]=max(f[H-h[i]][S-s[i]])需用借$
$f[H][S]=max(f[H-h[i]-(s[i]-S)][0])不需要借$

code :

int n,H,S;
int h[N],s[N],w[N];
ll f[N][N];

void solve(){
	cin>>n>>H>>S;
	Fup(i,1,n) cin>>h[i]>>s[i]>>w[i];
	Fup(i,1,n){
		Fde(j,H,h[i]+1){
			Fde(k,S,0){
				//消耗
				if(k < s[i] && j+k > s[i] + h[i]){
					chmax(f[j][k] , f[j - h[i] - (s[i] - k)][0]+w[i]);
				}else if(k >= s[i]){
					chmax(f[j][k],  f[j-h[i]][k-s[i]] + w[i]);
				}
			}
		}
	}
	cout<<f[H][S]<<endl;

}

D.Dyson Box

题意 :
给定多个小方块 , 对于每次加入一个方块之后,我们进行 行合并 或者 列合并 , 询问之后形成的周长是多少

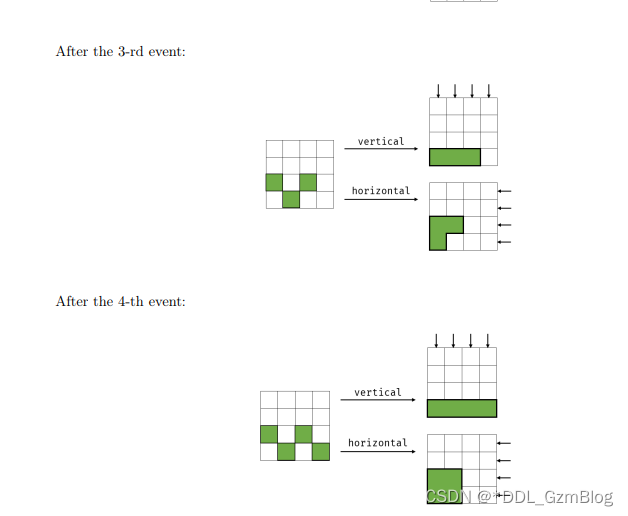
思路 :

因为题目范围的原因$1e5$,所以我们不考虑直接枚举或者是其他什么比较牛马的做法

因此我们只能对当下进行考虑 , 对于当前加进去的方块,我们考虑是否会被已经加过的影响

我们考虑一个方块的贡献是$4$ , 如果上下左右都有重叠那么显然这个方块的贡献就$-4$

因此我们类似递推的方式进行即可

code :

map<int,int> stx,sty;

void solve(){
	cin>>n;
	
	ll ansx = 0  ;
	ll ansy = 0  ;
	Fup(i,1,n){
		// cin>>x[i]>>y[i];
		cin>>x>>y;
		
		
		ansx += 4;
		ansy += 4;
		
		if(stx[x]) ansx -= 2;
		if(sty[y]) ansy -= 2;
		//上下 或者是 前后
		
		if(stx[x] < stx[x-1]) ansx -= 2;
		if(stx[x] < stx[x+1]) ansx -= 2;
		//左右
		
		if(sty[y] < sty[y-1]) ansy -= 2;
		if(sty[y] < sty[y+1]) ansy -= 2;
		//左右
		
		stx[x] ++ , sty[y] ++ ;
		cout<<ansx<<" "<<ansy<<endl;
	}

}

C. Cat Virus

题意 :

给你一个$k$ , 表示 你需要构造一棵仅有$k$种染色方法的树

染色的规则如下 :

我们选用黑白两色进行染色 , 如果当前节点是黑色,那么其儿子节点必须是黑色

思路 :
我们小画一下 , 就会发现对于儿子节点每个贡献2种选法 , 而其父亲节点计算的话那么就是 2*2*2…的形式+1

这个也很好理解即兄弟节点之间不受影响,所以我们可以直接乘法原理

那么我们根据这个性质,我们就可以对于每层开辟一个节点。之后对于能$/2$的,那么我们就对当前层开辟多个兄弟节点即可

code :

void dfs(int u,ll val){
	 //当前层要一个节点
	 ll temp = val - 1;
	 
	 //如果可以整除那就再这层继续分
	 if(temp%2 == 0){
	 	while(temp%2 == 0 && temp){
	 		temp/= 2;
	 		g[u].pb(++cnt);
	 	}
	 }

	 // if(temp == 0) return ;
	 	 
	 if(temp == 1) return;
	 //全白 不进行染色
	 
	 g[u].pb(++cnt);//开辟下一个节点
	 
	 dfs(cnt,temp);
	 	
}
void solve(){
	cin>>k;
	cnt = 1;
	dfs(1,k);
	cout<<cnt<<endl;
	
	Fup(i,1,cnt){
		for(auto x : g[i]){
			cout<<i<<" "<<x<<endl;
		}
	}
}