Machine Learning ~ looking for function

1. different types of functions

• Regression: output a scalar

• Classification: classes → correct one

• 黑暗大陆：structured learning - 创造

2. how to find the function - training data

1. function with unknown parameters - Model
   $$y=b+w{x}_1$$
   based on domain knowledge

   w and b are unknown parameters(learned from data)

   x1 - features

   w - weight

   b - bias

2. Define Loss from Training data

   Loss is a function of parameters. Loss means how good a set of values is.
   $$L(b,w)=\Sigma \frac{1}{n}{e}_n$$
   e: 预计值与真实值(Label)间的差距，计算方法很多

   • MAE: mean absolute error
     $$y=|y-\hat{y}|$$

   • MSE: mean square error

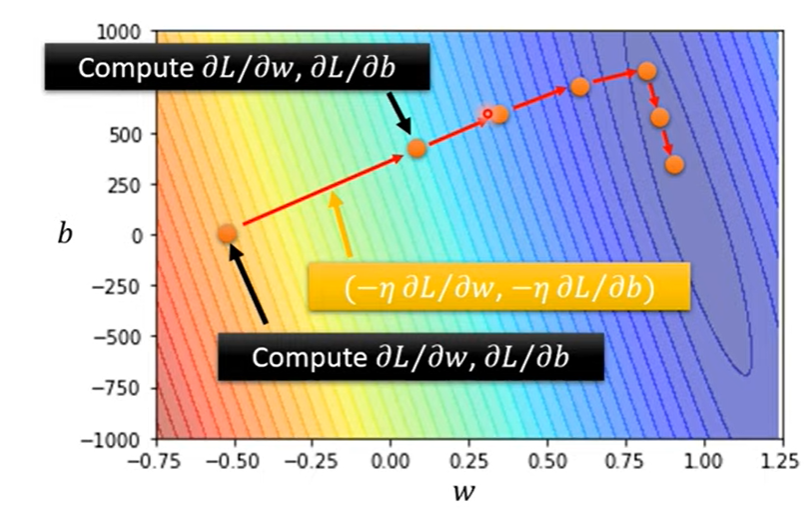
3. Optimization

   Gradient Descent

   
   • hyperparameters

   直到微分为0或你已经失去耐心

   问题非常明显：并未找到真正的global minima而是停留在一个Local minima.

   但事实上，Local minima是个伪命题，后续详谈。

   推广至两个参数：

   

   直观来看

   

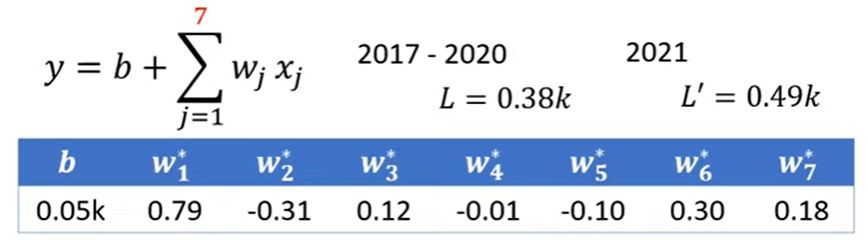
3. unseen during training

观察到7天一循环 于是

这样的模型叫做Linear models. 这样简单的线性关系有Model Bias，我们需要更flexible的模型

All piecewise linear curves =

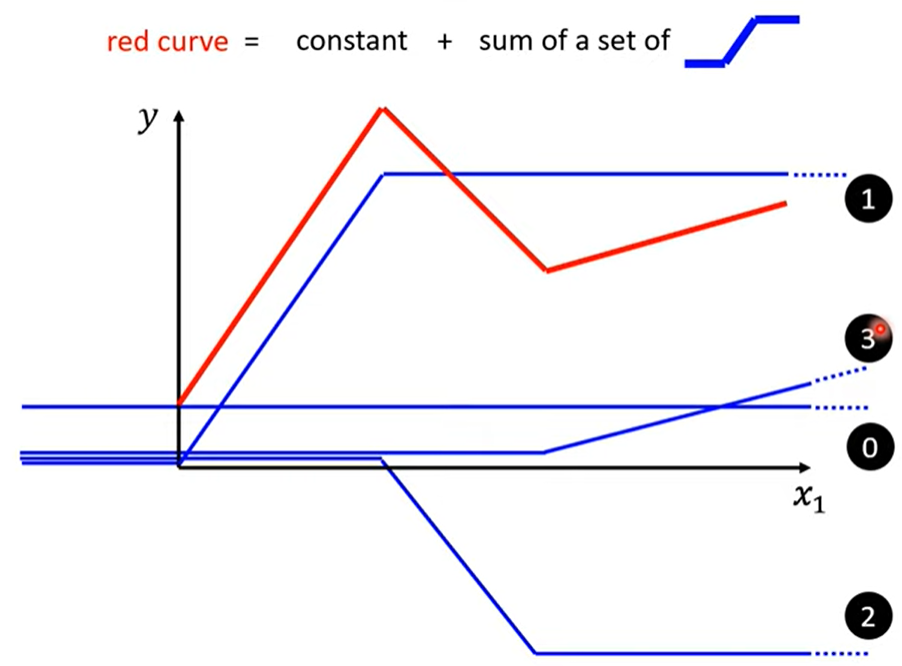
piecewise linear curve(hard Sigmoid)可以用来逼近continuous curve

x1趋近正无穷，y趋近于c；x趋近于负无穷，y趋近于0.

不同的w c b造出不同的sigmoid function，叠加出复杂的piecewise linear curve，从而逼近各种曲线

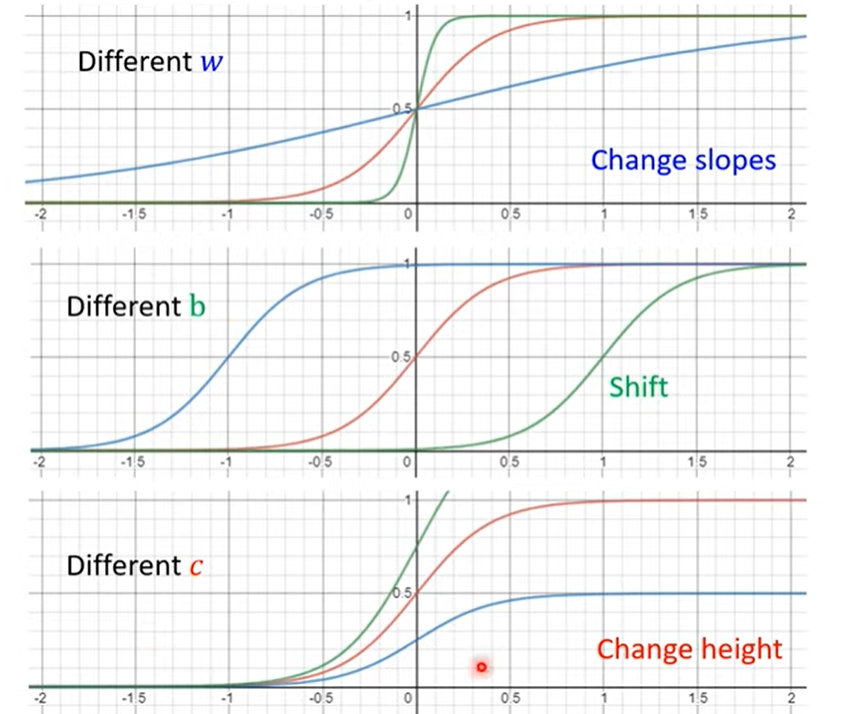
于是我们可以通过如下含有不同参数的公式，来逼近

推广至多天(more features)

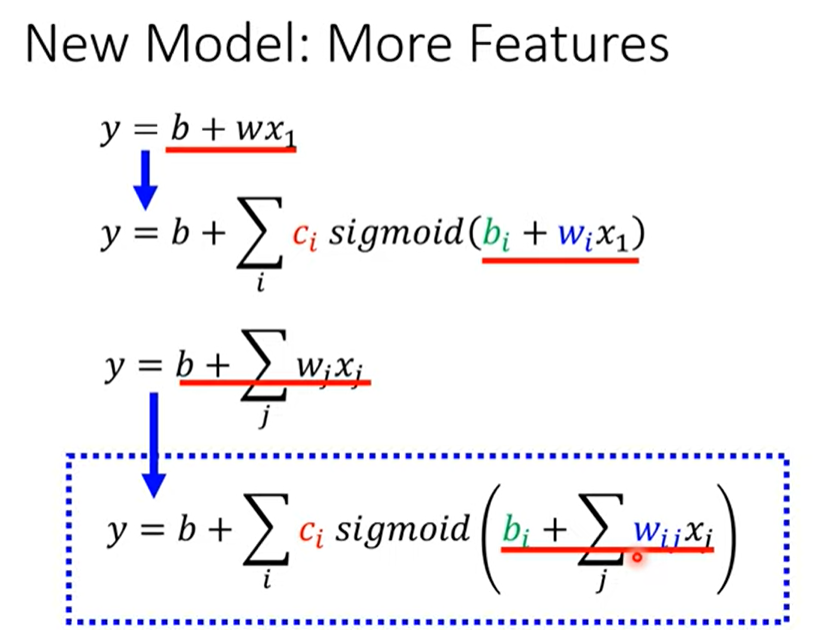
4. Back to ML Framework

4.1 Step1: function with unknown

每个 i 表示蓝色的function(hyperparameter)，j表示features

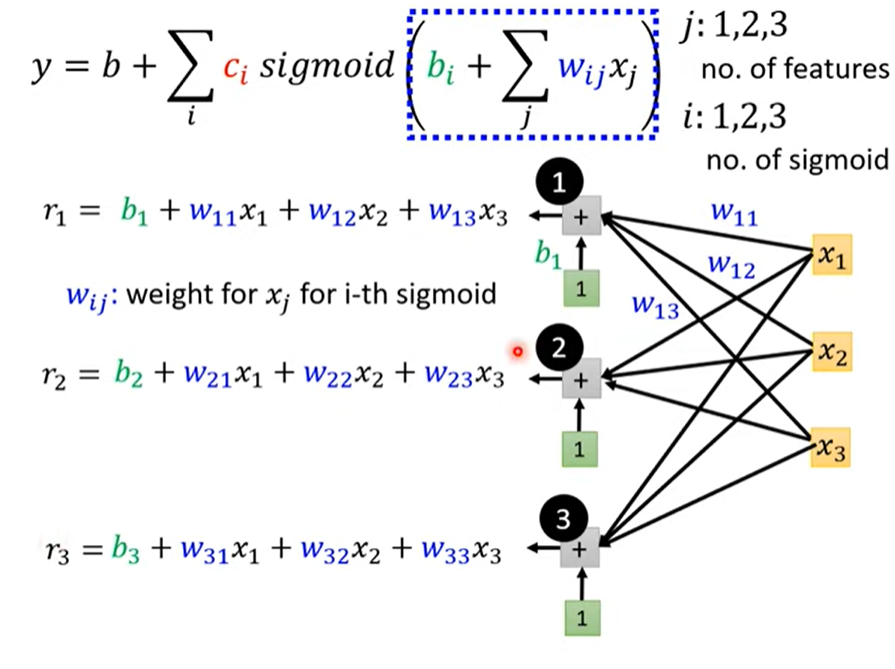
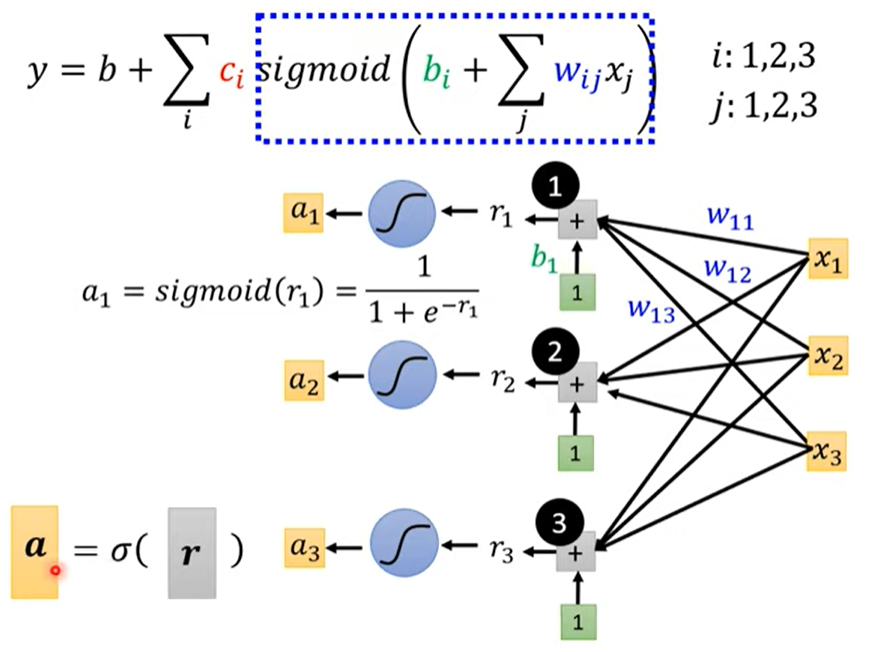
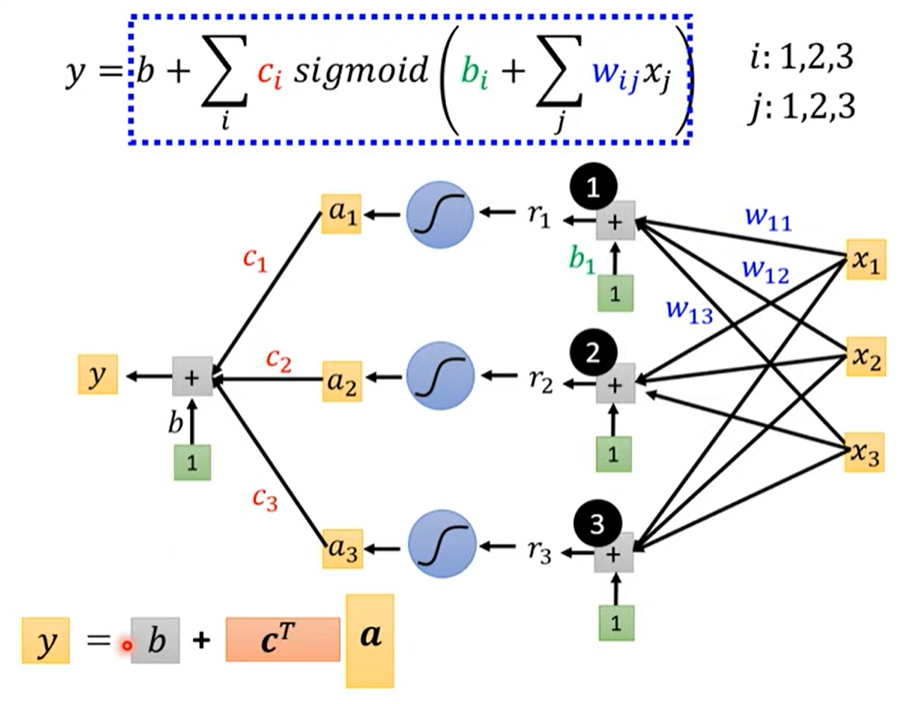
综上，用线性代数的矩阵表示

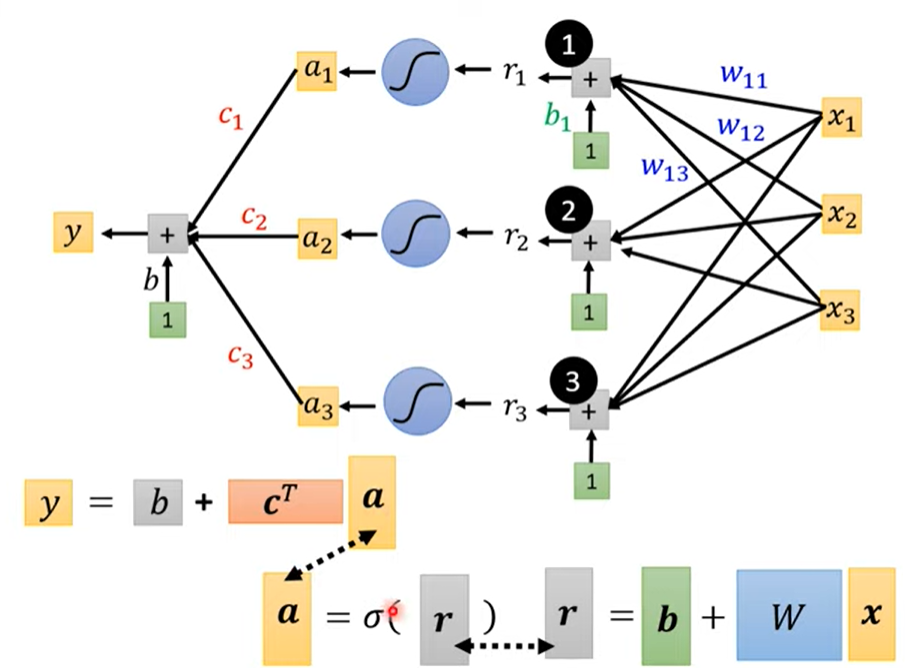
把unknown parameters拉直拼成一个长向量

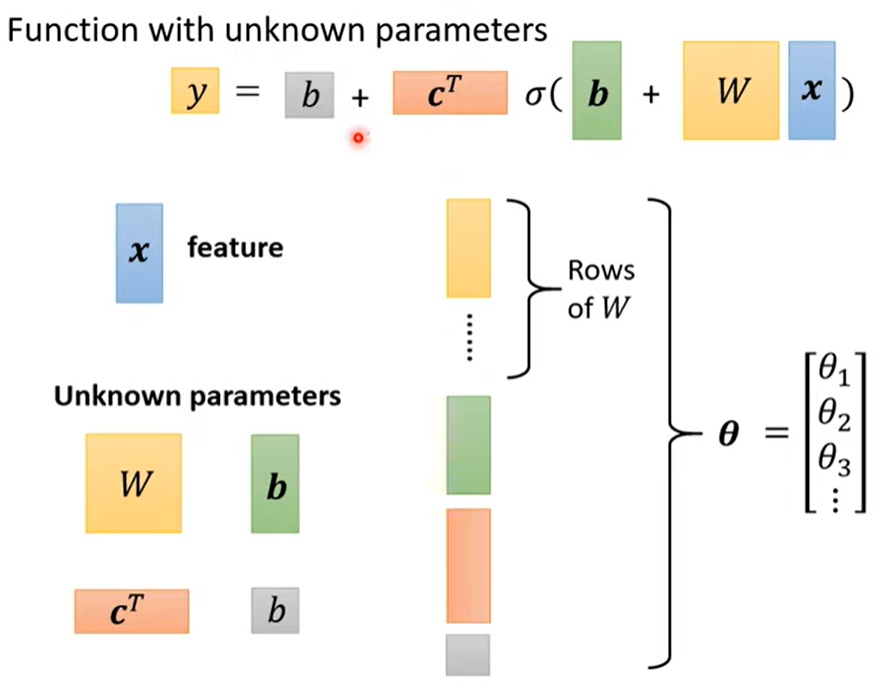
4.2 Step2: define loss from training data

只不过现在Loss的参数多了
$$L(\theta )$$
Loss means how good a set of values is.

4.3 step3: optimization

gradient 求梯度，并更新参数

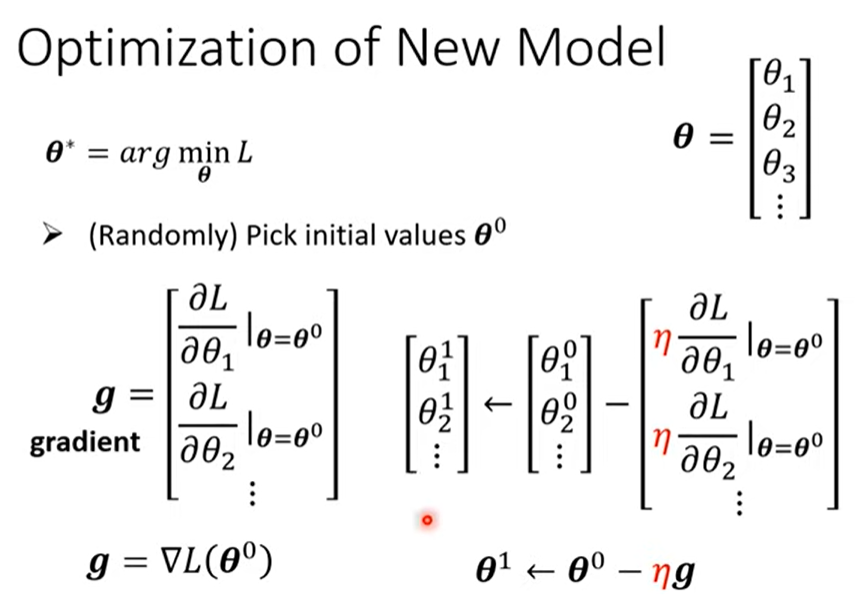
直到不想做了/得到零向量(实际上不太可能)

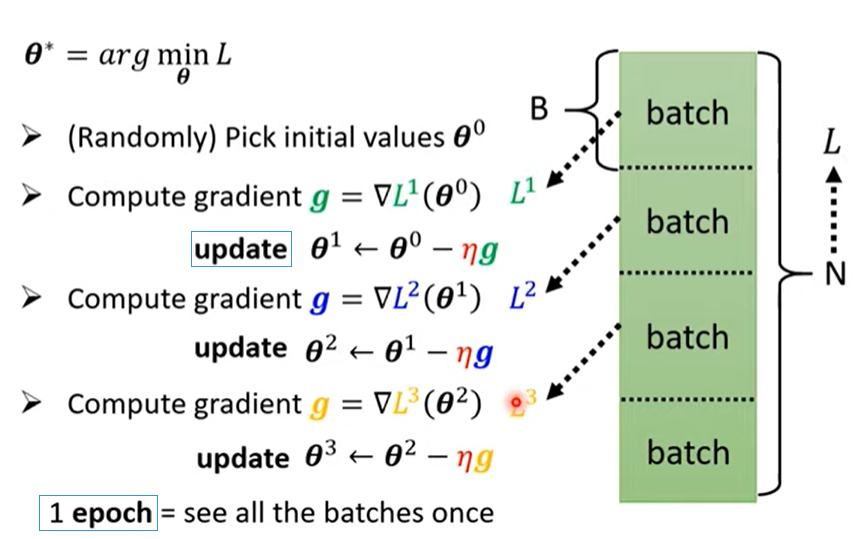
至于为什么要分成一个一个的batch(多少个也是hyperparameter)，后续详谈

4.4 其他

4.4.1 Sigmoid → ReLU

两个ReLU叠加起来成为一个Hard sigmoid

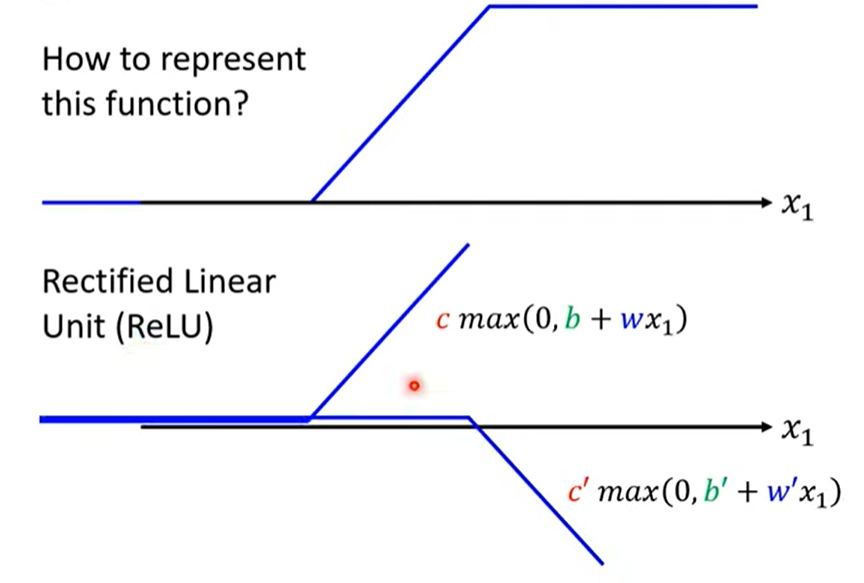
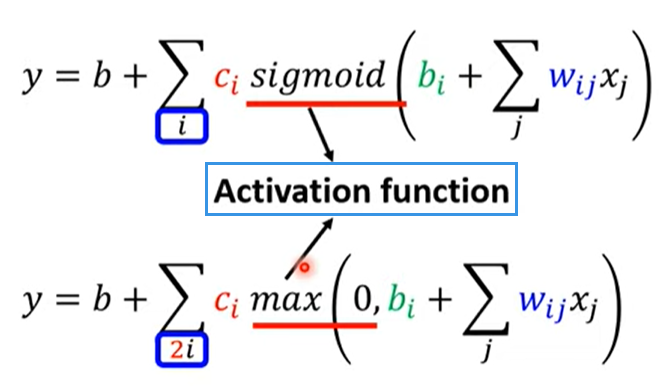
(max效果较好，原因以后详谈)

4.4.2 more variety of models

反复多做几次(几次，又是一个hyperparameter)

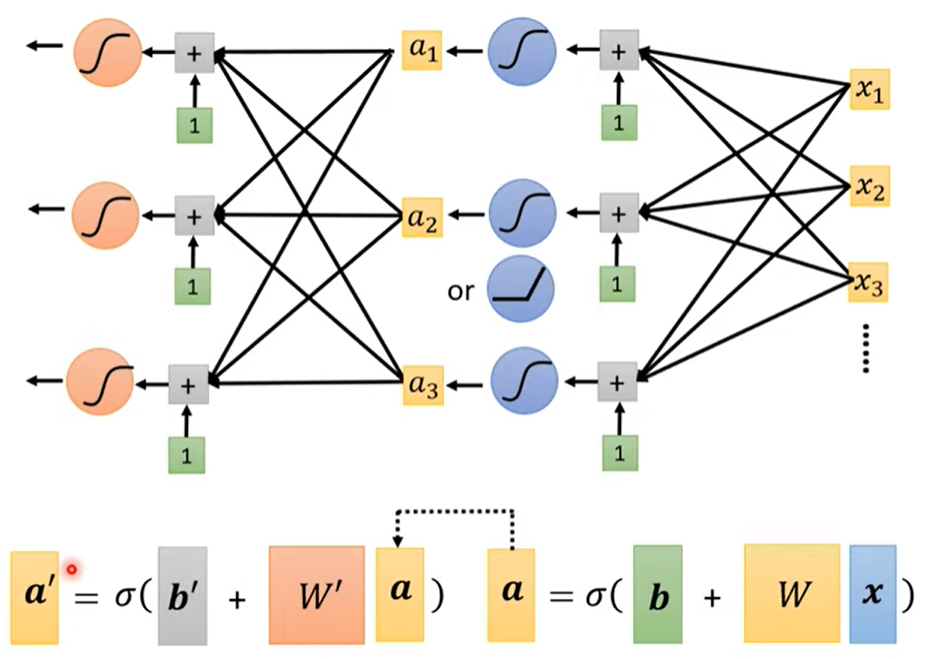
5. 神经网络 → 深度学习？！

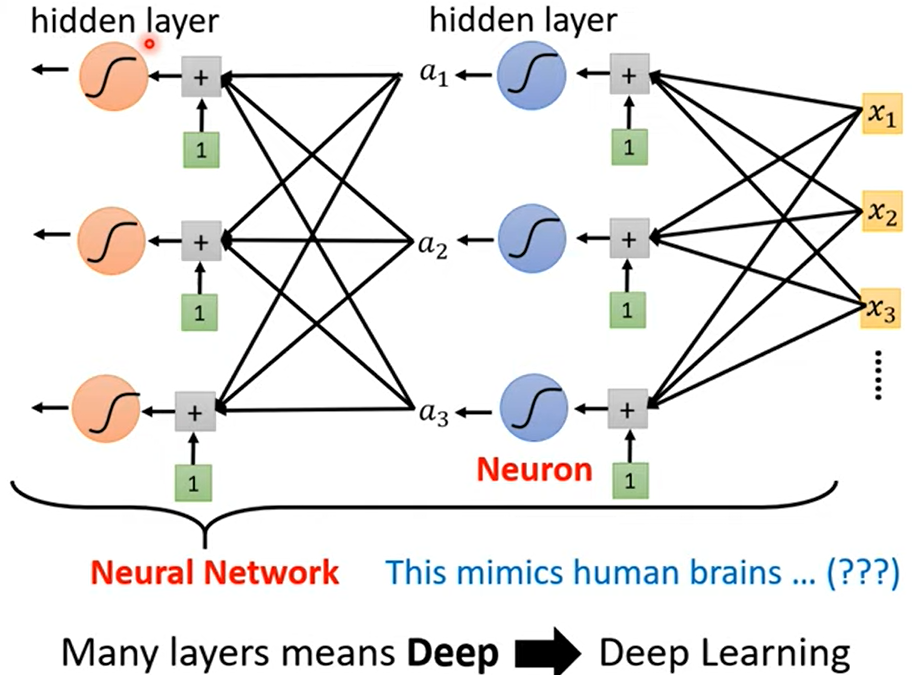
overfitting: Better on training data, worse on unseen data.