双指针算法
介绍
双指针算法分为两大类:
-
两个指针指向两个不同序列,用两个指针维护某一种逻辑,例如归并排序
-
两个指针指向一个序列,即用两个指针维护一段区间,例如快排
核心思想:
若能证明出题目存在单调逻辑,则可以利用单调逻辑,优化O(n^2)的朴素算法,使之变成双指针算法
- 单调逻辑:假定i和j是维护
[j, i]区间的端点,如果在枚举过程中随着i不断增大,j只会增大或不变,不会减小,那么就说明题目具有单调的逻辑,可以尝试使用双指针算法。 - 证明单调:一般证明题目的单调逻辑可以采用反证法——假如题目
(j,i)的情况不成立,那么右端点为i+1时,就不可能有(j,i+1),(j-1,i+1),(j-2,i+1),…,(0,i+1)的情况发生,只可能出现(j+1,i+1),(j+1,i+1),…,(i+1,i+1)的情况
模板代码:
// 朴素算法:O(n^2)
for( int i = 0; i < n ; i++)
{
for( int j = 0 ; j <= i ; j++)
{
if(check(i, j))
{
// 题目逻辑
// PASS
}
}
}
// 利用单调逻辑,将上面的算法优化到O(n)
// 换言之,本身需要枚举n^2种情况,但是可以优化到n种情况
// 双指针算法:O(n^2)
for( int i=0,j=0; i<n; i++)
{
while(j <= i && check(i, j)) j++;
// 题目逻辑
// PASS
}
例题
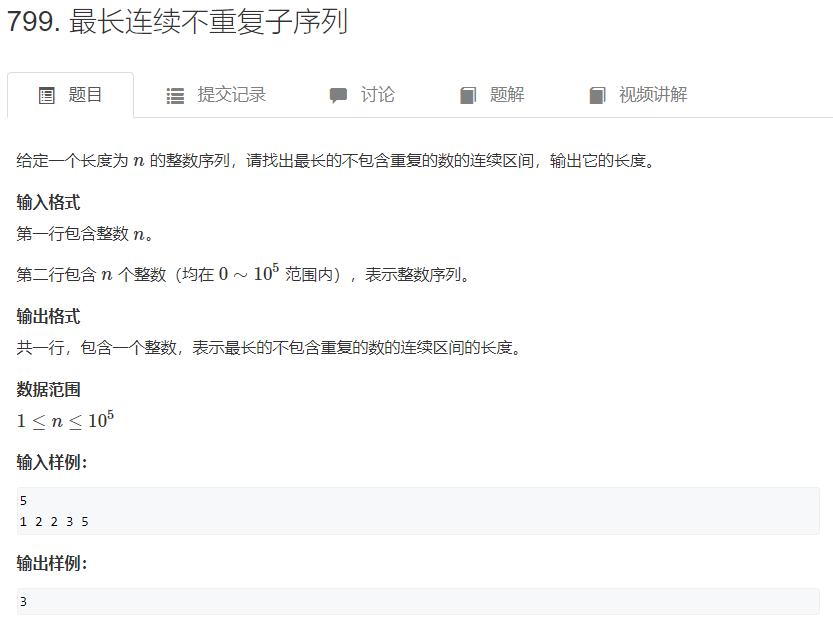
思路:
我们就用样例的1 2 2 3 5举例,如果采用朴素算法,将所有情况枚举一遍,那么会枚举出1+2+3+4+5=15种情况
但是这些情况,有一些是可以省略掉的。因为我们仔细考虑会发现题目存在单调逻辑。
该题中,如果一个区间不符合规律,那么包含该区间的所有区间都不符合逻辑。举个例子,假如区间称为[j,i]我们枚举1 2 2中的2 2,即1 (2 2),此时区间[1,2]很明显不符合条件,那么往后包含[1,2]区间的区间一定是不符合条件的。所以在==i从2往后枚举时,j只能取比1大的值==,这就是单调逻辑
因此我们只需要枚举右端点i,找到给定i下的最长不重复连续区间,保留此时的j,在后面的枚举中只需要将j在前面的基础上后移即可
代码:
#include<iostream>
using namespace std;
const int N =10e5+10;
int q[N],s[N]; // q[N]存放输入数据,s[N]存储维护区间数值出现次数
int main()
{
int n; cin >> n;
int res = 0;
// 输入
for(int i=0; i<n; i++) cin >> q[i];
// 双指针
for(int i=0,j=0; i<n; i++)
{
s[q[i]] ++ ; // 区间右侧新增q[i],计数器加1
while(s[q[i]] > 1) // 判断读入的数是否存在
{
s[q[j]] -- ;// 去除区间左侧的数
j++;// 区间左端点右移
}
res = max(res, i-j+1);// 记录区间最大值
}
cout << res;
}