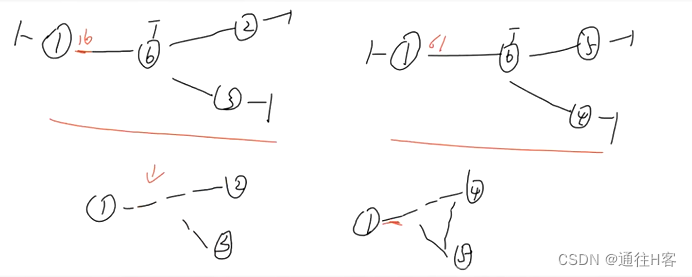厚积薄发打卡Day112：堆栈实践（二）＜汉诺塔问题＞

问题

相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

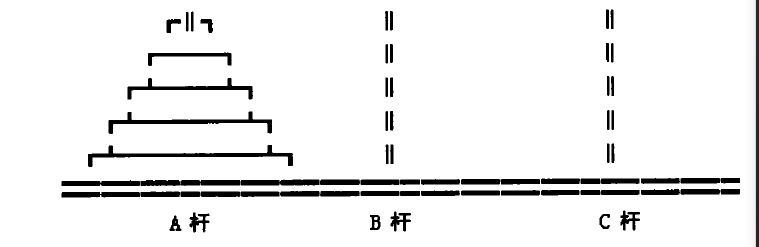
图1：汉诺塔问题图示

思路

在这个问题中我们得先定义三个塔：
1. 起点
2. 辅助塔
3. 终点
注意：上面三个塔的定义是相对的
汉诺塔必经的三个过程：

在这里插入图片描述

必经的三个步骤：

将n-1个盘子从【起点塔】移向【辅助塔】
将第n号盘子从【起点塔】移向【终点塔】
将n-1个盘子从【辅助塔】移向【终点塔】

举例：

在这里插入图片描述

数学归纳：

从上面的步骤可以看出 n-1个盘子移动了两次，n号盘子移动了一次
可以推导公式：

F(n) = 2F(n-1)+1

代码

public class Hanoi {

    // 步骤计数器
    private static int count;

    public static void main(String[] args) {
        while (true) {
            System.out.println("请输入盘子的数量：");
            Scanner scanner = new Scanner(System.in);
            int num = scanner.nextInt();
            count = 0;
            hanoi(num, "A", "B", "C");
            System.out.println("至少需要移动：" + count + " 步");
            System.out.println();
            move(num, "A", "B", "C");
        }
    }

    /**
     * @param num 总盘数
     * @param start 起始塔
     * @param help 辅助塔
     * @param end 终点塔
     */
    private static void hanoi(int num, String start, String help, String end) {
        count++;
        if (num == 1) {
            // 最终情况，将最后一个盘子从起始塔移向目标塔
            System.out.printf("%d 号 盘子从 [%s] -> [%s]%n", num, start, end);
        } else {
            hanoi(num - 1, start, end, help);
            // 将 n-1个盘子 从起始塔移动到 辅助塔
            // hanoi(1, start, help, end);
            System.out.printf("%d 号 盘子从 [%s] -> [%s]%n", num, start, end);
            hanoi(num - 1, help, start, end);
        }
    }
}

请输入盘子的数量：
3
1号 盘子从 [A] -> [C]
2号 盘子从 [A] -> [B]
1号 盘子从 [C] -> [B]
3号 盘子从 [A] -> [C]
1号 盘子从 [B] -> [A]
2号 盘子从 [B] -> [C]
1号 盘子从 [A] -> [C]
至少需要移动：7 步

请输入盘子的数量：
4
1号 盘子从 [A] -> [B]
2号 盘子从 [A] -> [C]
1号 盘子从 [B] -> [C]
3号 盘子从 [A] -> [B]
1号 盘子从 [C] -> [A]
2号 盘子从 [C] -> [B]
1号 盘子从 [A] -> [B]
4号 盘子从 [A] -> [C]
1号 盘子从 [B] -> [C]
2号 盘子从 [B] -> [A]
1号 盘子从 [C] -> [A]
3号 盘子从 [B] -> [C]
1号 盘子从 [A] -> [B]
2号 盘子从 [A] -> [C]
1号 盘子从 [B] -> [C]
至少需要移动：15 步