根据下面这道题讲下并查集
(其实本来是写题解的…写着写着就变成算法说明了)
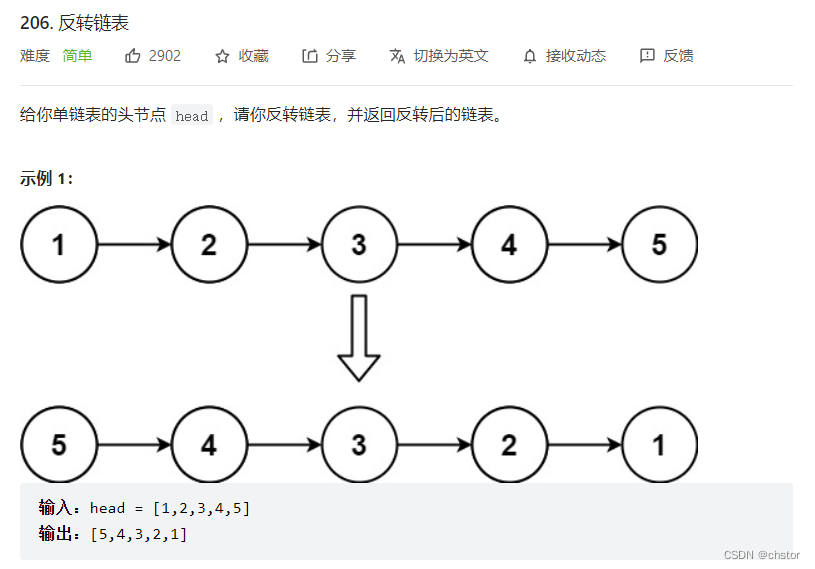
[蓝桥杯 2017 国 C] 合根植物(C++,并查集)
题目描述
w 星球的一个种植园,被分成 m × n m \times n m×n 个小格子(东西方向 m m m 行,南北方向 n n n 列)。每个格子里种了一株合根植物。
这种植物有个特点,它的根可能会沿着南北或东西方向伸展,从而与另一个格子的植物合成为一体。
如果我们告诉你哪些小格子间出现了连根现象,你能说出这个园中一共有多少株合根植物吗?
输入格式
第一行,两个整数 m m m, n n n,用空格分开,表示格子的行数、列数( 1 < m , n < 1000 1<m,n<1000 1<m,n<1000)。
接下来一行,一个整数 k k k,表示下面还有 k k k 行数据 ( 0 < k < 1 0 5 ) (0<k<10^5) (0<k<105)。
接下来 k k k 行,第行两个整数 a a a, b b b,表示编号为 a a a 的小格子和编号为 b b b 的小格子合根了。
格子的编号一行一行,从上到下,从左到右编号。
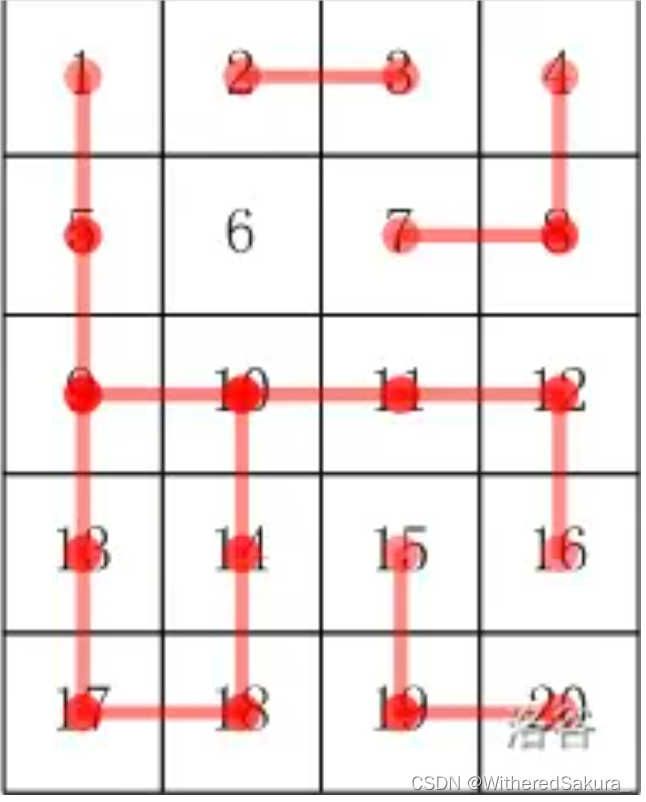
比如: 5 × 4 5 \times 4 5×4 的小格子,编号:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
17 18 19 20
输出格式
一行一个整数,表示答案
样例 #1
样例输入 #1
5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17
样例输出 #1
5
提示
样例解释
时限 1 秒, 256M。蓝桥杯 2017 年第八届国赛
解题思路:
emmm我也不知道该怎么引入,直接进行说明吧
并查集实现的就是合并两个元素(也可以是集合)成为一个集合
首先我们要知道如何辨别一个集合
我们知道一棵树所有子节点的根节点是相同的,换言之,根节点可以代表一棵树,抽象一点,就可以代表一个集合
那么如何寻访根节点呢?
int find(x) {//寻访节点x的根节点
if (father[x] == x)//x是根节点
return x;
else//x不是根节点
return find(father[x]);//寻访x的父节点
}
这个递归,应该…很好理解吧
但是如果一棵树的深度过深的话会导致寻访很慢,于是我们进行路径压缩
int find(x) {//寻访节点x的根节点
if (father[x] == x)//x是根节点
return x;
else {//x不是根节点
father[x] = find(father[x]);//路径压缩
return father[x];//寻访x的父节点
}
}
就是把所有子节点都连到根节点上
可以将以上代码优化
int find(x) {
return x == father[x] ? x : (father[x] = find(father[x]));
}
学会了辨别一个集合,接下来学习如何合并两个元素(或集合)
void merge(int x, int y) {
father[x] = father[y];
}
当然前提是判断两个元素不在一个集合中
bool is_same(int x, int y) {
if (find(x) == find(y)) return true;//一个集合
else return false;//两个集合
}
至此本题讲解完…好像没完,用递归寻访根节点会被卡掉
接下来介绍优化寻访的另一种方法,按秩合并
寻访慢的原因就是树的深度过深,我们希望深度尽可能的浅,这就是按秩合并的基本思想
void merge(int x, int y) {
if (depths[x] <= depths[y]) {//如果x是更简单的树
father[y] = father[x];//连接简单树到复杂树上
}
else father[x] = father[y];
if (depths[x] == depths[y])
depths[y]++;//如果深度相同,y的深度++,可以自行思考一下为什么(很简单的)
}
使用按秩合并记得要把所有元素的深度初始化为1
最后简单说明一下题意就可以明白了
其实二维的平面是假想的,直接维护一个m*n大小的数组就可以了
寻访根节点可以修改为while循环,大多数返回后没有指令的递归都可以优化为while不定循环
最后,AC代码如下
//并查集
#include <iostream>
using namespace std;
const int max_m = 1000;
const int max_n = 1000;
int ans;
int map[max_m * max_n] = { 0 };
int depths[max_m * max_n] = { 1 };
//寻访根节点
int find(int x) {
while (map[x] != x) x = map[x];
return x;
}
//按秩合并
void merge(int x, int y) {
if (depths[x] >= depths[y]) map[y] = map[x];
else map[x] = map[y];
if (depths[x] == depths[y]) depths[y]++;
}
int main() {
int m, n, k, u, v;
cin >> m >> n >> k;
int mul = m * n;
for (int i = 1; i <= mul; i++) {//初始化
map[i] = i;
depths[i] = 1;
}
ans = m * n;
for (int i = 0; i < k; i++) {//合并集合
cin >> u >> v;
int temp_1 = find(u);
int temp_2 = find(v);
if (temp_1 != temp_2) ans--;//集合数目-1
merge(temp_1, temp_2);
}
cout << ans;
return 0;
}