思路分析：

KMP算法是一种字符串匹配算法，他通过Next 数组能使i不回退，这样大大减少了无效的比对，提高了字符串匹配的速度。

Next数组：

要想让i不回退，就需要让j回退到合适的位置继续匹配，例如

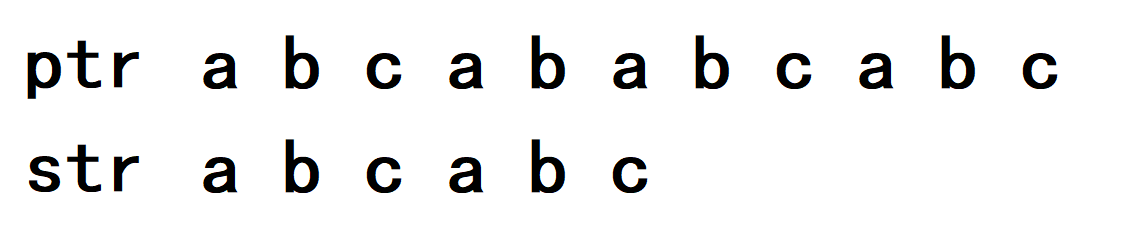
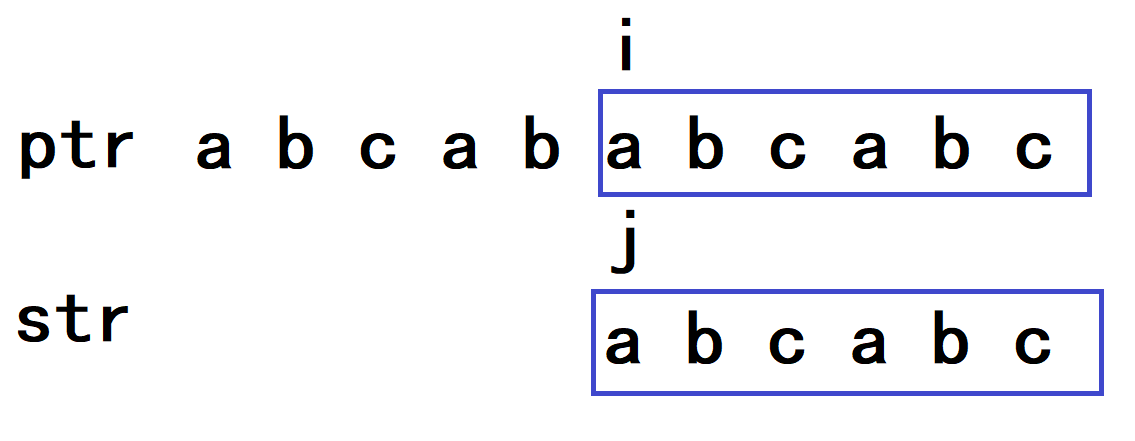
一开始ptr和str顺利互相匹配，i 和 j 会走到如图位置：

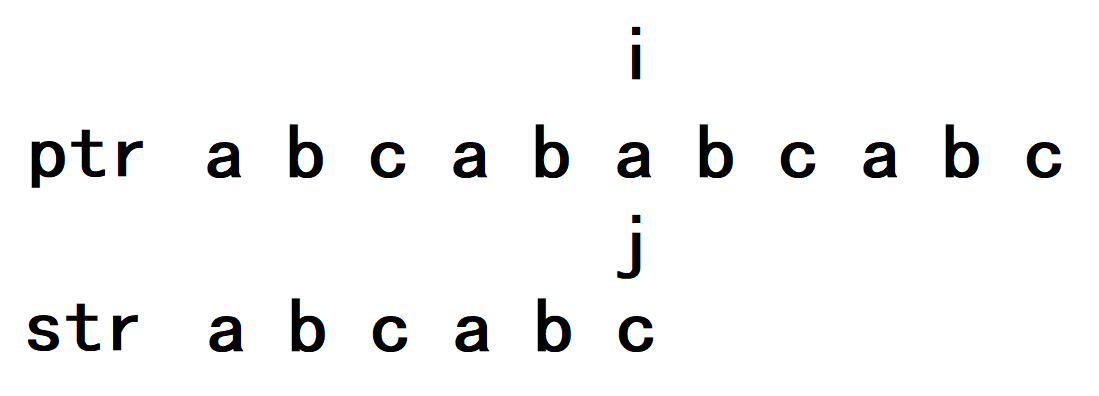
这时我们就不让i回退，而是让j回退到某个特殊位置，这个位置要能够让子串跳过的部分已经和主串相匹配，如图：

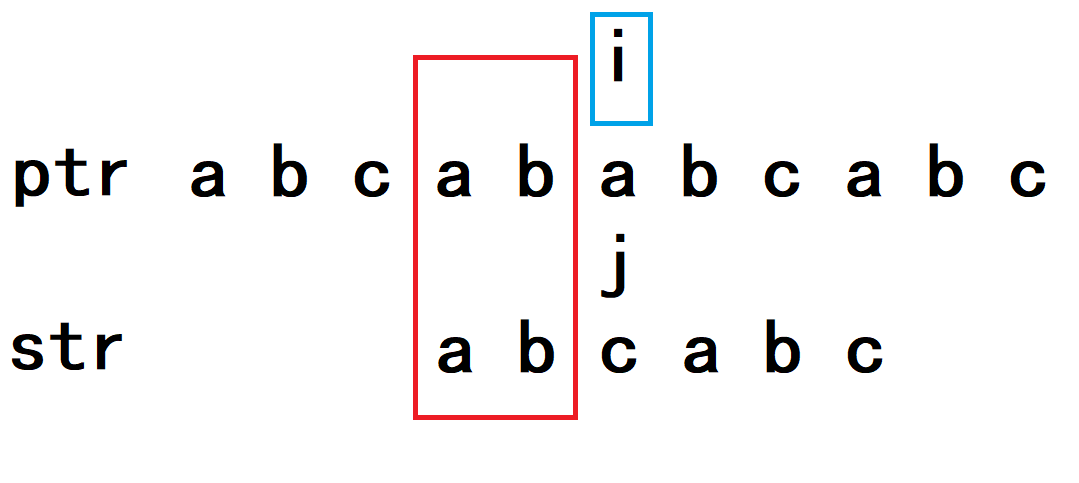
如图，i可以不回退j回退到c的位置，这样满足了子串跳过的部分（ab）已经和主串匹配：红色方框区域，我们只需要继续让i和j向后比较即可，我们发现主串和子串又不匹配，因此我们继续让j回退，如图：

这样我们能就很快速的不回退i就找到了对应的字符串。

我们发现，如果不回退i那么j的回退就变得很有讲究，第一次匹配失败后，我们把j回退到了下标为2的位置，我们为什么可以让他回退到下标为2的位置而不是从头开始？

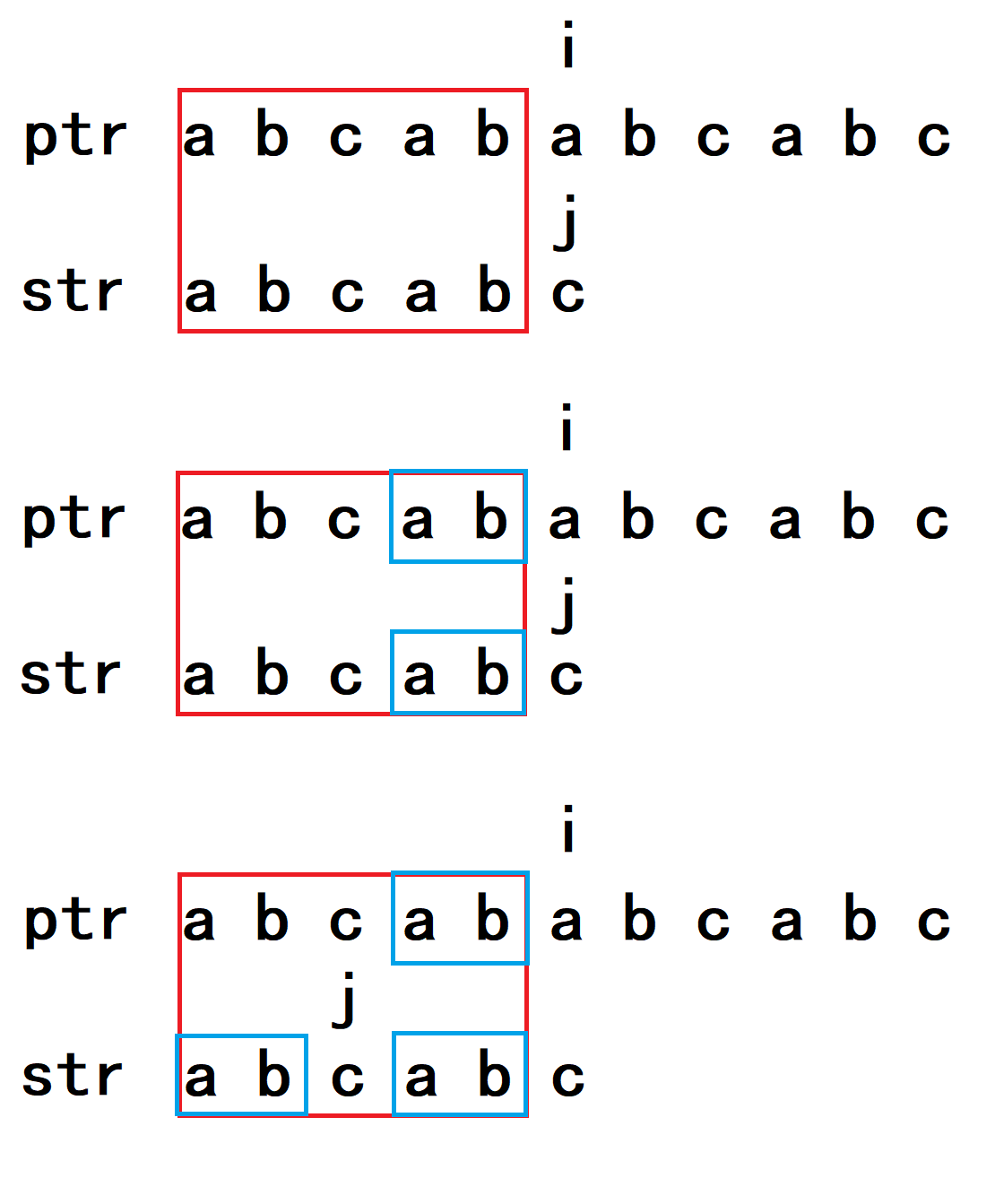
仔细看上图，如果能够走到j位置，就说明红色框框里的都已经匹配上了，进而说明上下两个蓝色框框内容是一样的，如果从头开始还能找到一个蓝色框框，那我们就可以省去比较蓝色框框里的元素，也就是图中的a b 。

其实，j要回退到哪个位置，取决于j之前走到了哪个位置，也取决于子串本身，如上图中的子串，j走到了下标为5的位置，这也就说明前面的元素已经和主串匹配，恰巧在已经匹配了的五个元素中，还有一对相同的串：ab ，这样我们就可以直接让j回退到上图中的位置

因此我们可以得出一个结论：在i 和 j 匹配不上的时候，j应该回退到哪里，取决于子串本身，与主串没有直接关系

由上面的分析我们可以总结一下回退的位置

下面我们来看一个新的子串

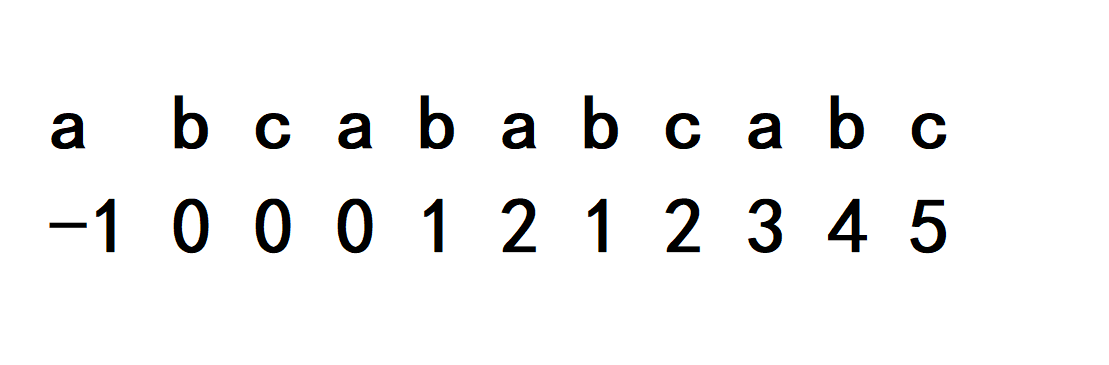
按照我们的逻辑，下面的数字是j匹配到对应位置后如果不匹配j回退的位置，也就是我们经常说的Next数组（另第一个位置是-1，在程序中在对逻辑进行控制）

观察Next数组，我们会发现一个规律，Next数组中有些位置是递增的，比如1 2 3 4 5

但有些位置却又不是递增的，如1 2 1，这里的规律是什么呢

我们不妨先来观察一下间断的位置，很明显我们能看出来是两个蓝色框框不一样导致了i+1位置没有连续下去：

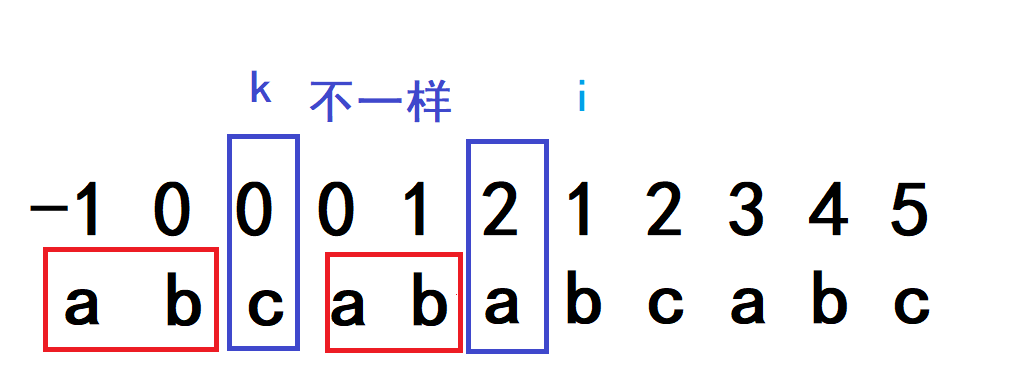
我们再来观察一下连续的情况：

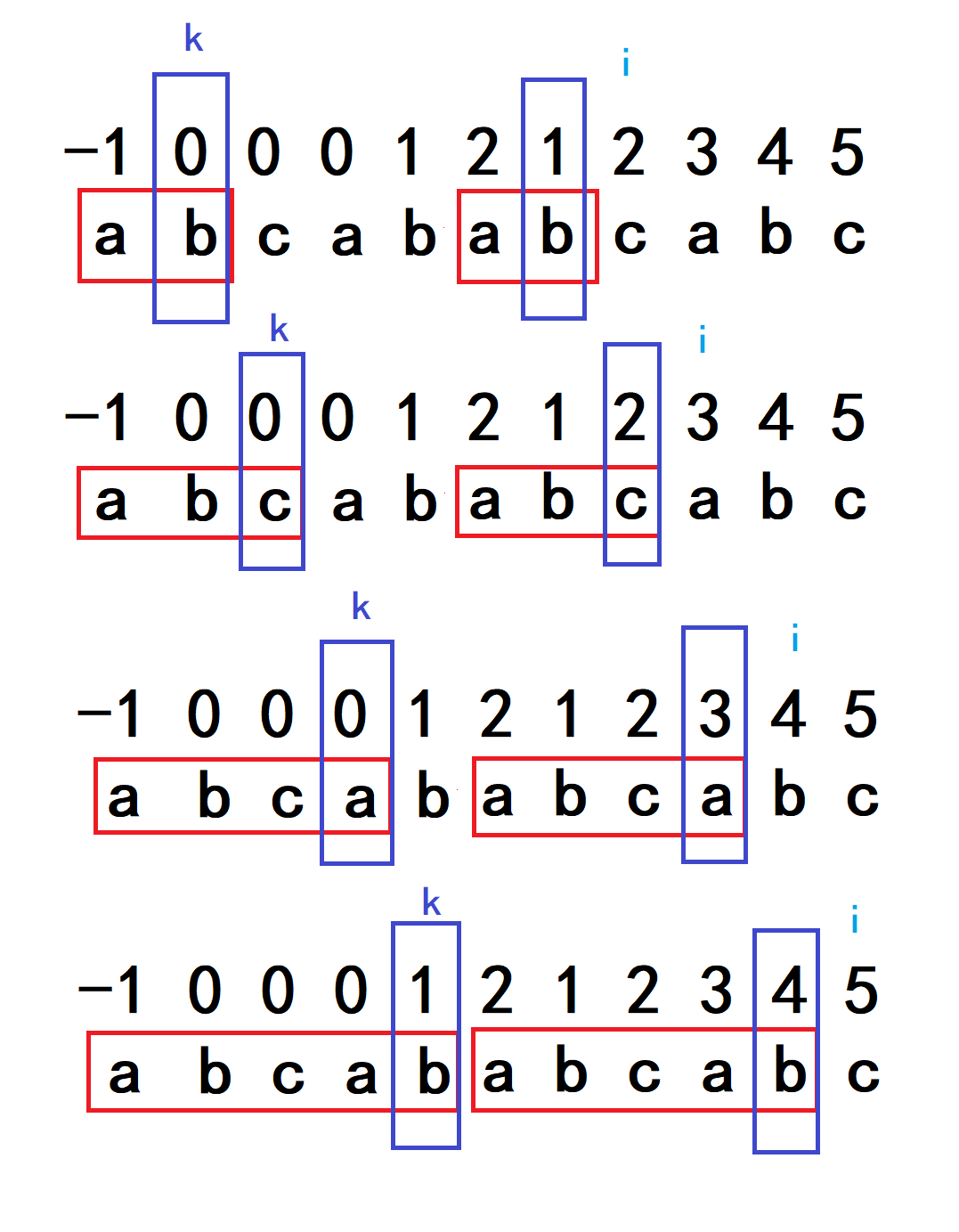
相信这样很直观的感受到正是因为紫色框框对应的两个元素不一样了，所以才导致没有连续起来，而如果紫色框框处一样，自然就会连续起来。

那没有连续起来的位置怎么知道要回退到什么地方呢？我们知道Next数组中存的数字是要回退的位置也就是找到[0~k][x~i-1]这两个最大且相同的字符串，

其中i-1-x = k-0 由此我们发现：x由k的位置决定，因此我们只需要让k继续回退到能连续的位置即可

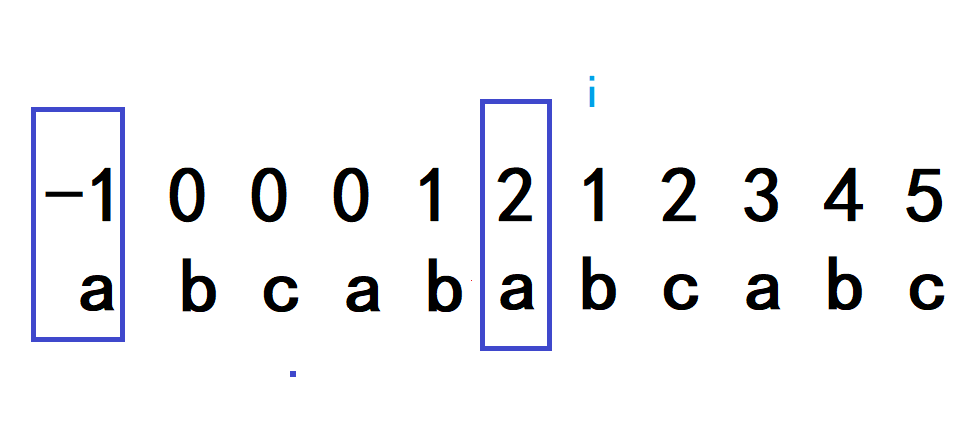
代码实现：

讲到这里相信大家已经明白了Next数组的本质和求法，接下来我们用代码来实现一下：

void GetNext(char* sub,int* next,int lenSub)
{
    next[0] = -1;
    next[1] =  0;
    int k = 0;
    int i = 2;

    while(i<lenSub)
    {
        if (k == -1 || sub[i - 1] == sub[k])
        {
            next[i] = k + 1;
            i++; k++;
        }
        else
        {
            k = next[k];
        }
    }
}

int KMP(char* str,char* sub,int pos)
{
    assert(str!=NULL && sub!=NULL);
    int lenStr = strlen(str);//主串的长度
    int lenSub = strlen(sub);//子串的长度
    if (lenStr == 0 || lenSub == 0)        return -1;//任何一个长度为0，都不用找
    if (pos < 0 || pos>lenStr) return -1;//位置不对也不用找

    int* next = (int*)malloc(sizeof(int)*lenSub);
    //开辟next数组
    assert(next != NULL);

    int i = pos;//遍历主串
    int j = 0;//遍历子串

    while (i < lenStr && j < lenSub)
    {
        if (j == -1 || str[i] == sub[j])
        {
            i++; j++;
        }
        else
        {
            j = next[j];
        }
    }

    if (j >= lenSub) 
    {
        return i - j;
    }
    return -1;
}