在学习上一章后，我们对树加以限制，如果树的度为 2，那么就称这颗树为 二叉树 (binary tree)。

二叉树的性质

在一棵二叉树上，有一些重要的性质：

1. 第 i 层 (i∈N) 上最多有 2^(i−1) 个结点
2. 层次为 k(k∈N) 的树最多有 2^k−1 个结点
3. 如果叶结点的数量为 n0​ ， degree=2 的结点的数量为 n2​ ，则 n0=n2+1

如果将二叉树的每一层填满，那么这颗二叉树被称之为 满二叉树 (full binary tree)；如果这颗二叉树除最后一层外都是满的，且最后一层要么是满的，要么是右边缺少连续的若干结点，那么称这颗二叉树为 完全二叉树 (complete binary tree)。

 由于 full binary tree 与 complete binary tree 是特殊的二叉树，因此它们也有一些确定性的性质。我们假设总结点数为 k ，树的高度 (即树的层数) 为 h ，其中某一层为第 i 层，则有以下性质：

 

 二叉树的实现

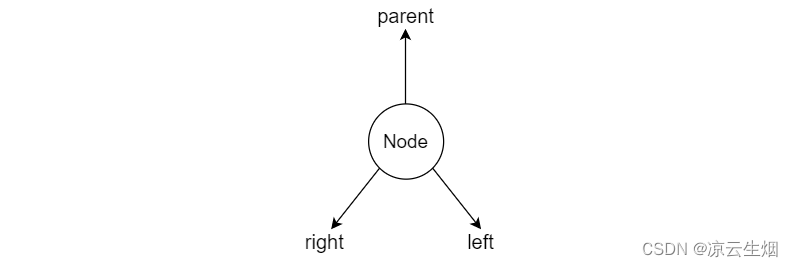
 为实现二叉树，我们可以为其采用双向链表的结构，但不再是指向结点的 prev 和 next，而是指向该结点的 left child 和 right child。

struct BinaryTreeBaseNode {
  BinaryTreeBaseNode* left,* right;
};
template <class Element>
struct BinaryTreeNode : BinaryTreeBaseNode {
  Element data;
};

在这里给出求解二叉树 root 中，node 的高度和深度

// 求解结点 node 的高度
int node_height(BinaryTreeBaseNode* node) {
  if (node == nullptr) {
    return -1;
  }
  return max(binary_tree_height(node->left),
             binary_tree_height(node->right)) + 1;
}
// 求解结点 node 在树 root 中的深度
int node_depth(BinaryTreeBaseNode* root, const BinaryTreeBaseNode* node) {
  if (root == nullptr) {
    return -1;
  }
  if (root == node) {
    return 0;
  }
  int left_depth = node_depth(root->left, node);
  int right_depth = node_depth(root->right, node);
  return left_depth == -1 ? (right_depth += right_depth != -1) : (left_depth + 1);
}

如果想要从结点向上求解某些数据时，并不容易做到，因为 child 没有指向 parent 的指针，需要遍历树找到 node 的 parent 才能操作。

// 求解结点 node 的 parent，如果不存在返回 nullptr
BinaryTreeBaseNode* get_parent(BinaryTreeBaseNode* root, const BinaryTreeBaseNode* node) {
  if (root == nullptr || root == node) {
    return nullptr;
  }
  if (root->left == node || root->right == node) {
    return root;
  }
  auto left = get_parent(root->left, node);
  return left == nullptr ? get_parent(root->right, node) : left;
}

为了方便实现我们自然而然的会在链域中添加指向 parent 的指针。这样在求解 sibling、 uncle 时十分方便，并且求解结点的深度时不再需要将其等价为 root 到 node 的路径长。需要注意的是，root 是没有 parent 的。

二叉树的遍历

还记得之前提到的 postorder traversal 与 preorder traversal 吗，它们对二叉树同样适用。不过先别急，既然现在 child 的数量确定了，能不能将对结点的处理放在两个结点的处理之间完成呢？当然没问题！这种处理方式就是 中序遍历 (inorder traversal)，当然这也是 DFS 的一种。

如果将当前结点标记为 N，左子结点标记为 L，右子结点标记为 R，那么前序遍历就可以表示为 NLR，中序遍历可以表示为 LNR，后序遍历可以表示为 LRN。

二叉树的前序遍历

recursion

void preorder(BinaryTreeBaseNode* root) {
  if (root == nullptr) {
    return;
  }
  process(root);
  preorder(root->left);
  preorder(root->right);
}

loop

void preorder(BinaryTreeBaseNode* root) {
  stack s;
  while (!s.empty() || root != nullptr) {
    while (root != nullptr) {
      process(root);
      s.push(root);
      root = root->left;
    }
    root = s.top();
    s.pop();
    root = root->rightl;
  }
}

二叉树的中序遍历

recursion

void inorder(BinaryTreeBaseNode* root) {
  if (root == nullptr) {
    return;
  }
  preorder(root->left);
  process(root);
  preorder(root->right);
}

loop

void preorder(BinaryTreeBaseNode* root) {
  stack s;
  while (!s.empty() || root != nullptr) {
    while (root != nullptr) {
      s.push(root);
      root = root->left;
    }
    root = s.top();
    s.pop();
    process(root);
    root = root->rightl;
  }
}

二叉树的后序遍历

recursion

void postorder(BinaryTreeBaseNode* root) {
  if (root == nullptr) {
    return;
  }
  preorder(root->left);
  preorder(root->right);
  process(root);
}

loop

在后序遍历中，在左子结点处理完成后，只有结点没有右子结点或右子结点处理完之后，才能对结点进行处理。因此需要判别当前结点的 右子结点为空 或 刚刚处理过的结点 是该结点的右子结点。判断右子结点为空十分简单，但是问题是如何记录刚刚访问过的结点？

利用一个变量指向正在处理的结点，当指向下一个待处理的结点时，其值就是该结点的上一个处理的结点，即处理前驱。

void postorder(BinaryTreeBaseNode* root) {
  stack s;
  BinaryTreeBaseNode* prev = nullptr;
  while (!s.empty() || root != nullptr) {
    while (root != nullptr) {
      s.push(root);
      root = root->left;
    }
    root = s.top();
    s.pop();
    if (root->right == nullptr || root->right == prev) {
      prev = root;
      process(root);
      root = nullptr;
    } else {
      s.push(root);
      root = root->right;
    }
  }
}

一个异构的前序遍历

如果你在对一个单词串进行翻转时，有一个简单可行的方法：先将单词串整体翻转，之后再逐词翻转。这样你就得到了一个对单词串的翻转！

 

这种异构的翻转也可以用在二叉树的 DFS 遍历上，前序遍历时遍历的结点顺序为 NLR (Node->Left->Right)，而后续遍历的结点顺序为 LRN ，对后续遍历的顺序进行翻转就变为了 NRL 。如果以 NRL 的顺序进行遍历，最后将结果翻转也可以得到一个后序遍历的序列，这本质上是一种前序遍历的异构。

二叉树的层序遍历

DFS 天生与 stack 结合在一起，而 BFS 与 queue 结合在一起。因此对于以上三种 DFS 遍历，使用 recursion 是一种简单、高效的理解与编码，而层序遍历则更适合于 loop。

void levelorder(BinaryTreeBaseNode* root) {
  queue q;
  q.push(root);
  while (!q.empty()) {
    for (int i = 0, cur_level_size = q.size(); i < cur_level_size; ++i) {
      root = q.front();
      q.pop();
      process(root);
      if (root->left != nullptr) {
        q.push(root->left);
      }
      if (root->right != nullptr) {
        q.push(root->right);
      }
    }
  }
}

Morris 遍历

在以上介绍的三种 DFS 遍历中，无论是 recursion 还是 loop 实现，都需要 O(N) 的时间复杂度与 O(N) 的空间复杂度。而 1979 年由 J.H.Morris 在他的 论文 中提出了一种遍历方式，可以利用 O(N) 的时间复杂度与 O(1) 的空间复杂度完成遍历。其核心思想是利用二叉树中的空闲指针，以实现空间复杂度的降低。

以 postorder 为例说明其算法的具体思路：

1. 如果当前结点的左子树为空，则遍历右子树
2. 如果当前结点的左子树不为空，在当前结点的左子树中找到当前结点在中序遍历中的前驱结点
   1. 如果前驱的右子结点为空，则将前驱结点的右子结点设置为当前结点，当前结点更新为其左子结点
   2. 如果前驱的右子结点为当前结点，则将其重新置空。倒序处理从当前结点的左子结点到该前驱结点路径上的所有结点。完成后将当前结点更新为当前结点的右子结点
3. 重复步骤 1、2 直到遍历结束

void __reverse_process(BinaryTreeBaseNode* node) {
  if (node == nullptr) {
    return;
  }
  __reverse_process(node->right);
  process(node);
}
void postorderTraversal(BinaryTreeBaseNode* root) {
  BinaryTreeBaseNode* cur = root,* prev = nullptr;
  while (cur != nullptr) {
    prev = cur->left;
    if (prev != nullptr) {
      while (prev->right != nullptr && prev->right != cur) {
        prev = prev->right;
      }
      if (prev->right == nullptr) {
        prev->right = cur;
        cur = cur->left;
        continue;
      }
      prev->right = nullptr;
      __reverse_process(cur->left);
    }
    cur = cur->right;
  }
  __reverse_precess(root);
}

 迭代器

既然可以遍历一棵树，那么依然希望可以在这棵树上暂停下来，对结点进行一些操作，再继续进行迭代。当我们选择的遍历方法不一样时，其迭代时的前驱与后继就不相同。

如果现在给定一个迭代器，应该如何找到迭代器的前驱与后继迭代器。这里给出求解中序遍历前驱的算法步骤与代码，求解中序遍历后继的算法与前驱的算法类似，因此只给出代码。

• 求解前驱
  • 如果结点的左子树存在，则前驱是结点左子树上最大的结点
  • 如果结点的左子树不存在，则需要寻找结点的 parent
    • 若结点是 parent 的右子树上的结点，则 parent 是其前驱
    • 若结点是 parent 的左子树上的结点，继续向上寻找，直到 parent 为 nullptr 或是其 parent 的右子树上的结点

// 寻找结点 node 的前驱
BinaryTreeBaseNode* get_previous(BinaryTreeBaseNode* node) {
  if (node->left != nullptr) {
    node = node->left;
    while (node->right != nullptr) {
      node = node->right;
    }
  } else {
    auto parent = get_parent(node);
    while (parent != nullptr && parent->left == node) {
      node = parent;
      parent = get_parent(parent);
    }
    node = parent;
  }
  return node;
}
// 寻找结点 node 的后继
BinaryTreeBaseNode* get_next(BinaryTreeBaseNode* node) {
  if (node->right != nullptr) {
    node = node->right;
    while (node->left != nullptr) {
      node = node->left;
    }
  } else {
    auto parent = get_parent(node);
    while (parent != nullptr && parent->right == node) {
      node = parent;
      parent = get_parent(parent);
    }
    node = parent;
  }
  return node;
}

 示例：表达式树

下图展示了一棵 表达式树 (expression tree)，leaf node 是操作数 (operand)，而 internal node 为运算符 (operator)。由于所有操作都是二元的，因此这颗树为二叉树。每个 operator 的 operand 分别是其两个子树的运算结果。

 

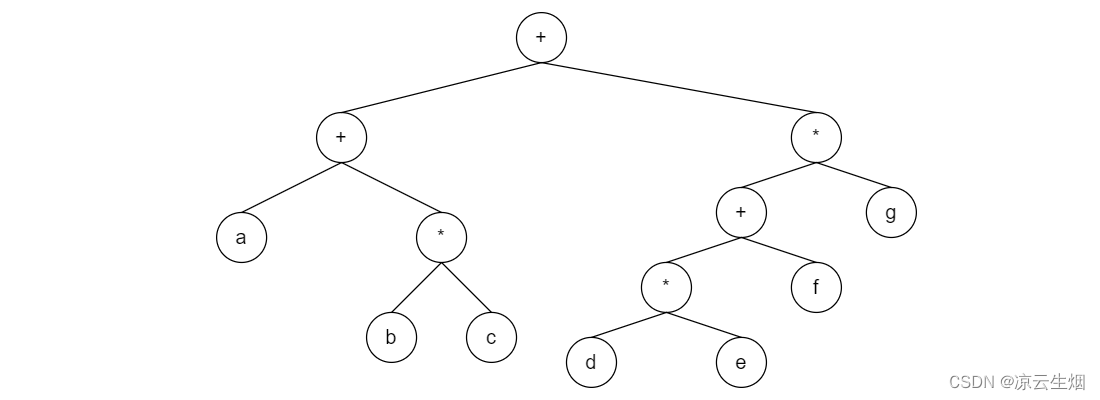
这个树对应的表达式为 a+b∗c+(d∗e+f)∗g ，如果我们对这颗树进行 postorder traversal 将得到序列 abc∗+de∗f+g∗+ ，这是一个后缀表达式；如果对其进行 preorder traversal，则会得到前缀表达式 ++a∗bc∗+∗defg ；最后试一下 inorder traversal，其结果应该是中缀表达式，不过其序列并没有带括号。

从 postorder traversal 的结果，可以很轻松的构建其这棵树。留给读者进行实现，这里将不再说明。