许多科学问题都要求以几何图形（geometric graphs）的形式处理数据。与一般图数据不同，几何图显示平移、旋转和反射的对称性。研究人员利用这种对称性的归纳偏差（inductive bias），开发了几何等变图神经网络（GNN），以更好地描述几何图的几何特性和拓扑。尽管取得了丰硕的成果，但它仍然缺乏一项survey来描述等变GNN是如何发展的，这反过来又阻碍了等变GNNs的进一步发展。为此，基于必要但简明的数学预备知识，我们下面分析并将现有方法分为三组，以了解如何表示GNN中的消息传递和聚合。另外还举例了相关应用，以便于以后的方法开发和实验评估研究。

---

归纳偏差or归纳偏置（inductive bias），归纳是自然科学研究中的一种方法，指的是从一些例子中寻找共性，形成一个通用的规则，bias是指我们对模型的偏好。因此归纳偏置可以理解为：

• 从现实生活中观察到的现象中归纳出一定的规则，然后对模型做一定的约束，从而可以起到"模型选择"的作用，即从假设空间中选择出更符合现实规则的模型。（可以理解为一个正则化方式）

关于等变与不变：

• 等变性（equivariant），对于一个特征，进行变换：$$f(g(x))=g(f(x))$$则称变换为等变的。
• 不变性（invraiant），对于特征，进行变换：$$f(x)=f(g(x))$$则称变换$f$对变换$g$具有不变性。

等变，不变与CNN：

• CNN具有等变性和不变性。如果我们的输出是给出图片中猫的位置，那么我们将图片中的猫从左边移到右边，这种平移也会反应在输出上，我们输出的位置也是从左边到右边，那么我们则可以说CNN有等变性；如果我们只是输出图片中是否有猫，那么我们无论把猫怎么移动，我们的输出都保持"有猫"的判定，因此体现了CNN的不变性。
• 因此，CNN中的卷积操作中的参数共享使得它对平移操作有等变性，而pooling操作对平移有不变性。

---

1.Introduction

许多问题，尤其是物理和化学问题，需要以几何图的形式处理数据。与一般图数据不同，几何图不仅为每个节点分配一个特征，还分配一个几何矢量。例如，分子或蛋白质可以被视为几何图，其中原子的3D位置坐标是几何矢量；或者在一般的多体物理系统中，3D状态（位置、速度或自旋）是粒子的几何矢量。值得注意的是，几何图显示了平移、旋转和反射的对称性。这是因为无论我们如何将分子（或一般物理系统）从一个地方平移或旋转到另一个地方，控制原子（或粒子）动力学的物理定律是相同的。在处理这类数据时，必须将对称性的归纳偏差纳入模型的设计中，这推动了几何等变图神经网络（GNN）的研究。

GNN最初由Sperduti和Starita于1997提出，在深度学习的发展下，GNN在图结构建模方面表现出了突出的优势。虽然已经开发了丰富的结构，但大多数以前的GNN在几何上并不是等变的，因此不适合用于几何图。为了实现几何等变，人们提出了大量工作来改进GNN中的消息传递和聚合机制。

然而，鉴于取得了丰硕的成就，仍然没有一份survey来描述等变GNN是如何发展的。这不仅阻碍了外部研究人员迅速进入这一领域，还可能阻碍从现有论文中提取经验教训和新想法，供那些想进一步推动这一领域的研究人员使用。

2.Backgrounds

在本节中，将介绍两个关键因素，即图神经网络（GNN）和等变，作为讨论几何等变GNN的基础。

2.1.消息传递GNNs

GNNs已经被广泛用于处理关系数据。考虑$G=(V,E)$，每个节点$i$都被分配一个特征$h_i$，我们也可以为连接$i,j$的边设置edge feature $e_{ij}$。Gilmer在2017年改进了一个开创性的消息传递方案，以将主流GNN统一到一个通用架构中。它迭代地为每个节点（或边）进行消息计算和邻域聚合。一般来说，我们有：$$m_{ij}={\psi }_m(h_i,h_j,e_{ij})\text{\hspace{1em}(1)}$$ h i ′ = ψ h ( { m i j } j ∈ N ( i ) , h i ) (2) h_{i}'=\psi_{h}(\left\{m_{ij}\right\}_{j\in N(i)},h_{i})\tag{2} hi′​=ψh​({mij​}j∈N(i)​,hi​)(2)其中，$N(i)$是$i$的邻居节点集合（默认不包括自环），${\psi }_m$和${\psi }_h$是带参数的函数。Eq.1描述了消息的生成，Eq.2描述了消息的聚合与节点的特征更新。

2.2.等变性

设$X$和$Y$分别为输入和输出的向量空间，这两个空间之间赋予一组变换$G$：$$G\times X\to X,G\times Y\to Y$$函数 “$\varphi :X\to Y$” 被称为对应$G$的等变量（如果当我们对输入应用任何变换时，输出也会存在相同的变换或在某种可预测的行为下发生变化），我们可以定义：

定义1（等变性）：函数 “$\varphi :X\to Y$” 是G-equivariant，当：$$\varphi ({\rho }_X(g)x)={\rho }_Y(g)\varphi (x),\forall g\in G\text{\hspace{1em}(3)}$$其中，${\rho }_X$和${\rho }_Y$分别是输入和输出空间中的群表示（group representations），特别的，如果${\rho }_Y$是恒等式（比如常量）则$\varphi$被称为不变量。

定义2（Group representation）：群的表示是可逆线性映射$\rho (g):G\to V$，$g\in G$是群中的元素，同时它是线性的：$\rho (g)\rho (h)=\rho (g\cdot h),\forall g,h\in G$。

---

群表示可以理解为变换的表示。比如：

• $O(n)$表示旋转和反射组成的$n$维正交群；
• $SO(n)$是一个只包含旋转的特殊正交群；
• $E(n)$是由旋转、反射和平移组成的$n$维欧几里得群；
• $SE(n)$是一个由旋转和平移组成的特殊的欧几里得群；
• 上面所有的群都是Lie群的具体例子；

---

3.几何等变GNNs

本节首先描述几何图，然后总结有望处理此类数据的几何等变GNN。

3.1.几何图

在许多应用中，我们处理的图不仅包含拓扑连接和节点特征，还包含某些几何信息。以分子为例，每个原子都有一个特征$h_i\in R^H$（比如，电荷，质量等）和一个几何矢量${\text{x}}_i\in R^3$（比如位置或速度坐标）。当通过GNN处理此类数据时，我们可以将等变的归纳偏差注入到图模型中。

对于几何图，应用场景决定是否需要等变性，例如：

• 在预测分子的能量时，我们需要输出对几何矢量的任何旋转保持不变性（需要不变性）；
• 然而，在预测分子动力学时，我们要求输出与每个原子位置的输入相等（需要等变性）。

为了更好地区分，在下文中，用粗体表示几何矢量，用普通符号表示非几何量。

Eq.1-2被改为：$$m_{ij}={\psi }_m({\text{x}}_i,{\text{x}}_j,h_i,h_j,e_{ij})\text{\hspace{1em}(4)}$$$${\text{m}}_{ij}={\psi }_{\text{m}}({\text{x}}_i,{\text{x}}_j,h_i,h_j,e_{ij})\text{\hspace{1em}(5)}$$ h i ′ = ψ h ( { m i j } j ∈ N ( i ) , h i ) (6) h'_{i}=\psi_{h}(\left\{m_{ij}\right\}_{j\in N(i)},h_{i})\tag{6} hi′​=ψh​({mij​}j∈N(i)​,hi​)(6) x i ′ = ψ x ( { m i j } j ∈ N ( i ) , x i ) (7) \textbf{x}'_{i}=\psi_{\textbf{x}}(\left\{\textbf{m}_{ij}\right\}_{j\in N(i)},\textbf{x}_{i})\tag{7} xi′​=ψx​({mij​}j∈N(i)​,xi​)(7)其中，$m_{ij}$和${\text{m}}_{ij}$分别是通过边$(i,j)$传递的标量和方向输出，${\psi }_h$和${\psi }_{\text{x}}$分别是用于标量特征和几何矢量特征的消息聚合函数。另外：

• ${\psi }_m$对输入$({\text{x}}_i,{\text{x}}_j)$是G-invariant的；
• ${\psi }_{\text{m}}$对输入$({\text{x}}_i,{\text{x}}_j)$是G-equivariant的；
• ${\psi }_{\text{x}}$对输入 { m i j } j ∈ N ( i ) \left\{\textbf{m}_{ij}\right\}_{j\in N(i)} {mij​}j∈N(i)​和${\text{x}}_i$是G-equivariant的；

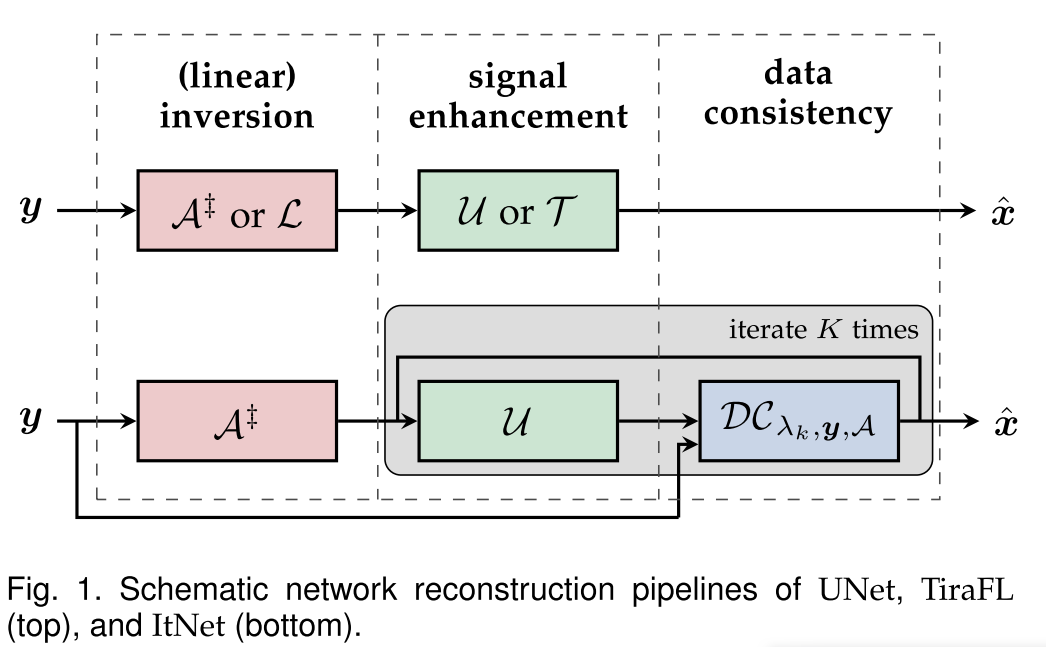
图1中详细说明了上述等变消息传递机制。

• 图1：旋转情况下几何等变消息传递的图示。生成标量消息和矢量消息，然后进行聚合，从而产生等变更新。

目前已经提出了多种等变GNNs，它们通常是不同Group上的 Eq.4-7 的不同具体对象。根据消息的表示方式，将当前的方法分为三类：不可约表示（irreducible representation），正则表示（regular representation），标量化（scalarization）。

在大多数情况下，由于相对位置${\text{x}}_i-{\text{x}}_j$是平移不变量（translation invariant），因此，下面讨论主要涉及旋转和除了平移的其他变换。

3.2.不可约表示Irreducible Representation

这类模型基于表示论中关于紧群的线性表示可以拆解为一系列不可约表示这一理论。从而在$SO(3)$群（$SO(n)$是一个只包含旋转的特殊正交群）中构建满足等变性的消息传递模型，例如：$${\text{m}}_{ij}^l=\sum _{k\ge 0}{\text{W}}^{lk}({\text{x}}_i-{\text{x}}_j){\text{x}}_j^k$$$${\text{x}}_i^{\prime l}=w_{ll}{\text{x}}_i^l+\sum _{j\in N(i)}{\text{m}}_{ij}^l$$上面模型对任意属于$SO(3)$的旋转操作等变。其中，${\text{x}}_i^l\in R^{2l+1}$表示节点$i$的 degree $l$ 几何向量。${\text{x}}_i\in R^3$是节点的坐标，$w_{ll}$是self-interaction权重，${\text{W}}^{lk}(\text{x})\in R^{(2l+1)\times (2k+1)}$是旋转可变的，具体实现为：$${\text{W}}^{lk}({\text{D}}^1(r)\text{x})={\text{D}}^l(r){\text{W}}^{lk}(\text{x})({\text{D}}^k(r){)}^{-1}$$

3.3.基于正则表示的模型

另一类的工作尝试利用群的正则表示来构建群卷积操作。比如Lie卷积：$$m_{ij}=\phi (log(u_i^{-1}{u}_j))h_j$$$$h_i^{\prime }=\frac{1}{|N(i)|+1}(h_i+\sum _{j\in N(i)}{m}_{ij})$$其中，$u_i$是${\text{x}}_i$在群中的映射元素，log将群元素映射到对应的Lie代数。$\phi$是一个MLP。通过这种构造，Lie卷积中对于$h_i$的更新实现了对于任意Lie群以及其离散子群的不变性。

3.4.标量化

除了基于群表示论的途径外，很多工作采用了基于标量化的建模等变性的方法。这类标量化的方法将几何特征转化为一些不变的标量，然后利用MLP网络结构来得到一个标量的变换，最后将这个变换加回到原有的几何特征上从而得到等变性。比如：$$m_{ij}={\phi }_m(h_i,h_j,||{\text{x}}_i-{\text{x}}_j|{|}^2,e_{ij})$$$${\text{x}}_i^{\prime }={\text{x}}_i+\sum _{j\ne i}({\text{x}}_i-{\text{x}}_j){\phi }_x(m_{ij})$$$$h_i^{\prime }={\phi }_h(h_i,\sum _{j\in N(i)}{m}_{ij})$$其中，$||{\text{x}}_i-{\text{x}}_j||$是对几何特征的标量化，$\phi$代表不同的MLP，通过将几何信息与非几何信息关联：$({\text{x}}_i-{\text{x}}_j){\phi }_x(m_{ij})$，可以同时保证非几何特征和几何特征传播过程中的等变性。这个构造结合了物理知识，可以看成是对两个粒子的库伦力 / 重力的计算的建模。

4.应用

等变GNN在从物理系统到化学物质的各种类型的real-world几何数据上有着广泛的应用。

物理动力学模拟

对复杂物理系统的动力学建模一直是一个具有挑战性的课题，神经网络已经被用于推断相互作用和动力学。在物理系统中，像带电粒子这样的物体通过遵循物理定律的力相互作用。通常任务是在初始条件下预测粒子的动力学，包括位置、速度和电荷。这样的任务是E(3)-等变的，因为粒子的动力学与整个系统一起平移、旋转和反射。

---

$E(n)$是由旋转、反射和平移组成的$n$维欧几里得群

---

分子

另一个重要的应用场景是分子数据，其中分子中的原子受到复杂的化学相互作用的影响。对于分子数据，标量节点特征$h_i$通常是原子的特征，节点之间的连接性要么由化学键提供，要么基于距离阈值获取。下面回顾分子的等变GNN，包括预测和生成。

预测
2022 年 7月18日腾讯 AI Lab发表了题为 “3D Equivariant Molecular Graph pretraining” 的文章，开发了基于能量表示的等变分子图神经网络预训练模型，在下游能量和力预测上均达到了最优的效果。

---

使用3D backbone模型，设计3D感知预训练任务，并针对下游任务进行评估，存在如下挑战：

• 如何保持生物世界的对称性旋转/平移分子的三维构象不会改变其行为规律。在数学上，应该使用backbone模型E(3)-等变和预训练损失E(3)-不变，其中，群E(3)包含旋转、反射和平移。

---

生成
Axelrod和Gomez Bombarelli引入了大规模未标记数据，将其分为两个子集GEOM-QM9和GEOM Drugs。这些数据集包含大量小分子构象的不同样本，并作为分子构象生成任务中的无监督训练集。ConfGF和DGSM使用旋转平移等变GNN参数化基于分数的生成模型中的分数函数，从而生成学习构象条件分布的生成模型。GeoDiff进一步将生成模型推广到去噪扩散模型。

蛋白质与小分子docking
预测药物样分子如何与特定蛋白质靶标结合是药物发现的核心问题。一种极快的计算binding方法将实现快速虚拟筛选或成为药物工程等关键应用。现有方法的计算成本很高，因为它们依赖于大量候选采样以及评分、排名和微调步骤。

“EquiBind:Geometric Deep Learning for Drug Binding Structure Prediction” 挑战了这一范式，这是一种 SE(3)-等变 几何深度学习模型，对：

• i) 受体receptor结合位置（盲对接）；
• ii) 配体ligand的结合姿势和方向进行直接预测。

与传统和最近的基线相比，EquiBind 实现了1200倍的加速。

• EquiBind架构：简单来说，该方法利用E(3)-等变网络生成配体和受体上的结合关键点，而后在三维空间中对这些点进行匹配来确定结合模式。同时，该网络还能够对配体的三维结构进行变换实现小分子柔性对接。