混淆矩阵回顾

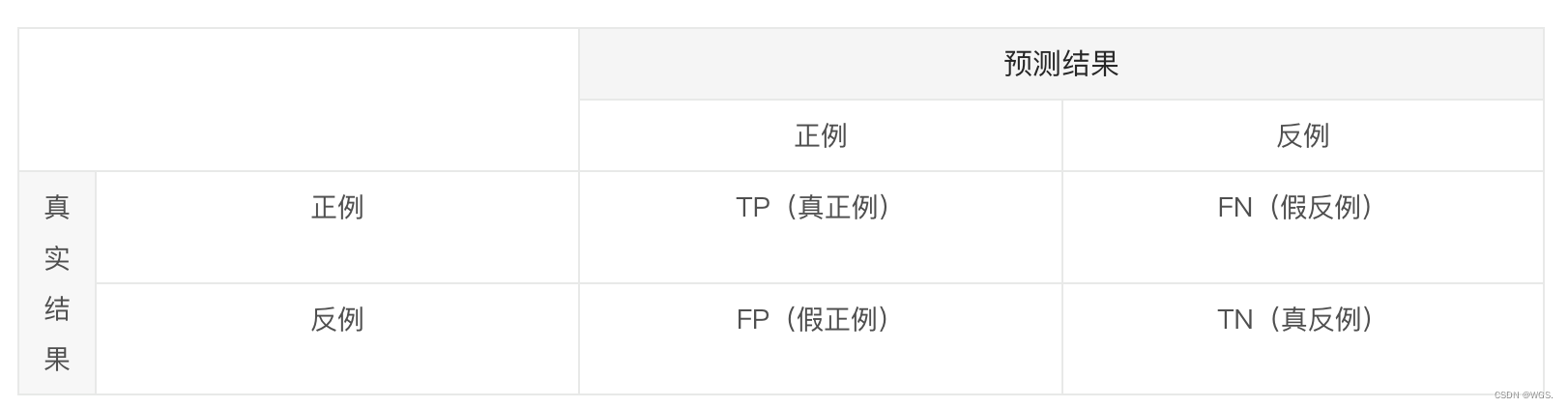
• 若一个实例是正类，并且被预测为正类，即为真正类，TP（True Positive）
• 若一个实例是正类，但是被预测为负类，即为假负类，FN（False Negative）
• 若一个实例是负类，但是被预测为正类，即为假正类，FP（False Positive）
• 若一个实例是负类，并且被预测为负类，即为真负类，TN（True Negative）

第一个字母T/F，表示预测的正确与否；第二个字母P/N，表示预测的结果为正例或者负例。TP就表示预测对了，预测的结果是正例，那它的意思就是把正例预测为了正例。

Precision、Recall、F1回顾

• 精确率（Precision、查准率）：针对预测结果而言，指的是所有预测为正的样本中实际为正的概率。
  $Precision=\frac{TP}{TP+FP}$

• 召回率（Recall、查全率）：针对原样本而言，指的是实际为正的样本中被预测为正样本的概率。
  $Recall=\frac{TP}{TP+FN}$

• F1：综合精确率和召回率：
  $F1=\frac{2\ast P\ast R}{P+R}$

举个例子：假设共有10张图片进行分类，其中有4张是狗。模型最终分出了5张狗，但是在这5张中，只有3张被正确识别为狗。
精确率为：3/5=60%，即分出的这5张，只有3张是对的；
召回率为：3/4=75%，即总共有4张狗图片需要识别，模型正确识别了3张。

多分类混淆矩阵

我们直接以3分类为例看下：

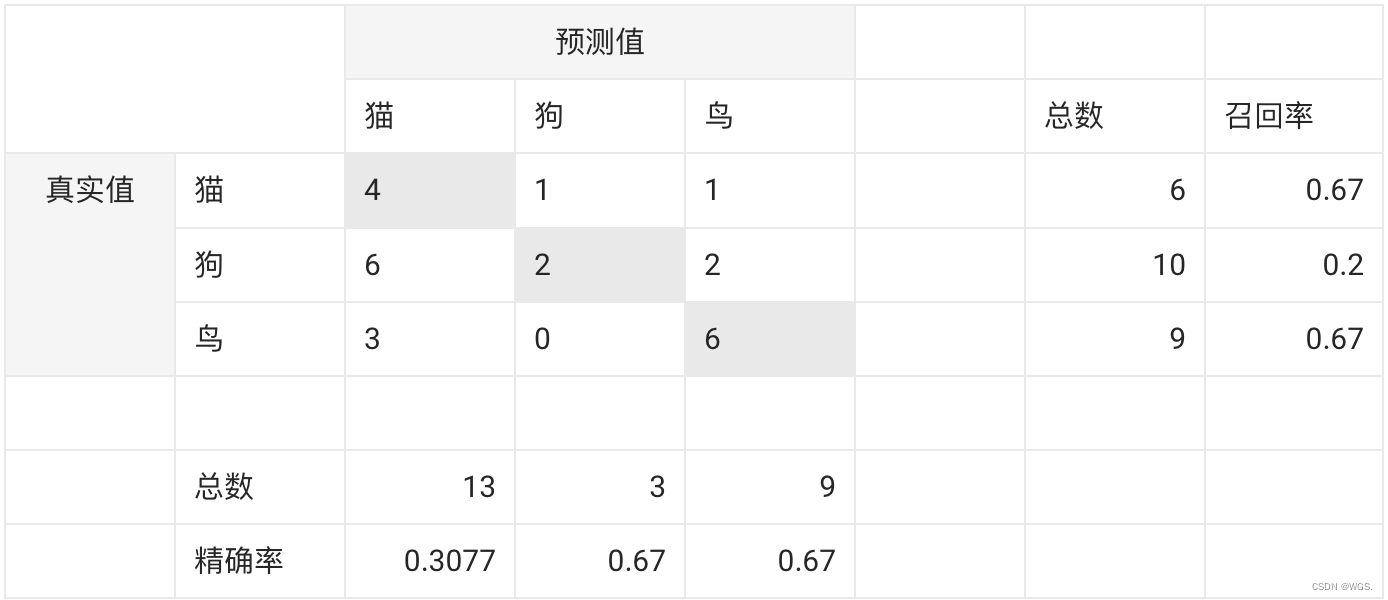
• 对角线的值表示分类器对该类别预测正确的个数；
• 每一横轴表示这个类别真实的样本数，猫共有6只、狗共有10只、鸟共有9只，样本总数为25；

对于猫来说：
$Precisio{n}_{猫}=\frac{4}{13}=0.3077$

$Recal{l}_{猫}=\frac{4}{6}=0.67$

对于狗来说：
$Precisio{n}_{狗}=\frac{2}{3}=0.67$

$Recal{l}_{狗}=\frac{2}{10}=0.2$

对于鸟来说：
$Precisio{n}_{鸟}=\frac{6}{9}=0.67$

$Recal{l}_{鸟}=\frac{6}{9}=0.67$

宏平均（Macro-average）

宏平均是直接将不同类别的指标加起来做平均，能够平等的看待每个类别，但是它的值会受到稀有类别的影响，会更加关注类别少的样本。

• 宏精确率 macroP：计算每个类别的精确率然后求均值：
  $macroP=\frac{1}{n}{\sum }_1^n{P}_i$
  $macroP=\frac{0.3077+0.67+0.67}{3}$

• 宏召回率 macroR：计算每个类别的召回率然后求均值：
  $macroR=\frac{1}{n}{\sum }_1^n{R}_i$
  $macroR=\frac{0.67+0.2+0.67}{3}$

• 宏F1 macroF1：
  $macroF1=\frac{2\times macroP\times macroR}{macroP+macroR}$

微平均（Micro-average）

与宏平均不同，微平均先将混淆矩阵的TP、FP、TN、FN对应位置求均值，然后再根据公式计算。

• 微精确率 microP：
  $microP=\frac{\overline{TP}}{\overline{TP}\times \overline{FP}}$

• 微召回率 microR：
  $microR=\frac{\overline{TP}}{\overline{TP}\times \overline{FN}}$

• 微F1 microF1
  $microF1=\frac{2\times microP\times microR}{microP+microR}$

加权平均（Weighted-average）

• 权重为各类别的占比：
  $w_i=\frac{sum(i)}{sum(class)}$

• 加权精确率 weightedP：
  $weightedP={\sum }_i{w}_i{P}_i$

• 加权召回率
  $weightedR={\sum }_i{w}_i{R}_i$

• 加权F1：
  $weightedF1=\frac{2\times weightedP\times weightedR}{weightedP+weightedR}$

总结

• 如果看重样本数量多的class，推荐微平均；
• 如果看重样本数量少的class，推荐宏平均；
• 如果微平均 远 低于宏平均，需要注意样本量多的class；
• 如果微平均 远 高于宏平均，需要注意样本量少的class。

代码

def adaptive_calculation(metric, pre_y, y, task='binary'):
    '''
    binary metric：accuracy、precision、recall、f1
    multiclass metric：accuracy、macro_p、macro_r、macro_f1、micro_p、micro_r、micro_f1、weighted_p、weighted_r、weighted_f1
    '''
    indict = {}
    indict['accuracy'] = metrics.accuracy_score(y, pre_y)
    if task == 'binary':
        for i in metric:
            if i == 'precision':
                indict['precision'] = metrics.precision_score(y, pre_y)
            if i == 'recall':
                indict['recall'] = metrics.recall_score(y, pre_y)
            if i == 'f1':
                indict['f1'] = metrics.f1_score(y, pre_y)
    elif task == 'multiclass':
        for i in metric:
            if i == 'macro_p':
                indict['macro_p'] = metrics.precision_score(y, pre_y, average='macro')
            if i == 'macro_r':
                indict['macro_r'] = metrics.recall_score(y, pre_y, average='macro')
            if i == 'macro_f1':
                indict['macro_f1'] = metrics.f1_score(y, pre_y, average='macro')
            if i == 'micro_p':
                indict['micro_p'] = metrics.precision_score(y, pre_y, average='micro')
            if i == 'micro_r':
                indict['micro_r'] = metrics.recall_score(y, pre_y, average='micro')
            if i == 'micro_f1':
                indict['micro_f1'] = metrics.f1_score(y, pre_y, average='micro')
            if i == 'weighted_p':
                indict['weighted_p'] = metrics.precision_score(y, pre_y, average='weighted')
            if i == 'weighted_r':
                indict['weighted_r'] = metrics.recall_score(y, pre_y, average='weighted')
            if i == 'weighted_f1':
                indict['weighted_f1'] = metrics.f1_score(y, pre_y, average='weighted')
    return indict