目录
一、栈概述
二、模拟实现栈
1、入栈
2、出栈
3、取栈顶元素
三、栈的应用
1、逆序打印链表
2、括号匹配问题
3、逆波兰表达式求值
4、栈的压入、弹出序列
5、最小栈
一、栈概述
栈(Stack)也是数据结构的一种,属于线性数据结构,栈最大的特点是“先进后出”,就是先进入栈的元素后出来,栈只能每次弹出栈顶元素,不能弹出处在栈中间的元素。
二、模拟实现栈
栈底层也是依据数组进行实现。
private int[] data;
private int usedSize;
public myStack(){
this.data=new int[10];
}1、入栈
将元素入栈首先要判断栈是否已满,如果满了就要扩容,否则就直接将元素插入到栈中,栈的长度加1。
//入栈
public void push(int val){
if(isFull()){
data= Arrays.copyOf(data,2*data.length);
}
data[usedSize++]=val;
}
//判断栈是否已满
public boolean isFull(){
if(usedSize==data.length){
return false;
}else{
return true;
}
}2、出栈
出栈就首先需要判断栈是否为空,如果未空则无法取元素,否则就取出栈尾元素,栈长度减1。
//出栈
public int pop(){
if(isEmpty()){
System.out.println("栈为空");
}
return data[--usedSize];
}
//判断栈是否为空
public boolean isEmpty(){
if(usedSize==0){
return true;
}
return false;
}3、取栈顶元素
与出栈不同,取栈顶元素只是拿到栈顶的元素,并不会让元素出栈,也需要判断栈是否为空。
//取栈顶元素
public int peek(){
if(isEmpty()){
System.out.println("栈为空");
}
return data[usedSize-1];
}在Java标准库中也只实现了以上方法,但是在用Stack类时却有许多方法,因为Stack类继承了Vector类,Vector类本身也实现了许多方法。
三、栈的应用
1、逆序打印链表
由于栈是先进后出的,所以就将链表中的元素全部入栈,再接着全部出栈。
//逆序打印链表
public void printList(ListNode head){
ListNode cur=head;
Stack<Object> stack = new Stack<>();
while(cur!=null){
stack.push(cur.val);
cur=cur.next;
}
while(!stack.empty()){
System.out.println(stack.pop());
}
}此处也可以通过递归来依靠链表直接打印。
//递归实现逆序打印链表
public void printList2(ListNode head){
if(head==null){
return;
}else if(head.next==null){
System.out.println(head.val);
}else{
printList(head.next);
System.out.println(head.val);
}
}2、括号匹配问题
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
解题思路:可以遍历字符串,遇到左括号则入栈,遇到右括号则取栈顶元素进行匹配,若匹配失败则直接返回false,否则继续向下遍历,如果出现栈为空但是仍有右括号或栈不为空,但是字符串已经遍历完的情况也需要返回失败。
public boolean isValid(String s) {
Stack<Character> stack=new Stack<>();
for(int i=0;i<s.length();i++){
char ch=s.charAt(i);
if(ch=='('||ch=='['||ch=='{'){
stack.push(ch);
}else{
if(!stack.isEmpty()){
char ch1=stack.peek();
if(ch1=='('&&ch==')'||ch1=='['&&ch==']'||ch1=='{'&&ch=='}'){
stack.pop();
}else{
return false;
}
}else{
return false;
}
}
}
if(!stack.isEmpty()){
return false;
}
return true;
}3、逆波兰表达式求值
给你一个字符串数组
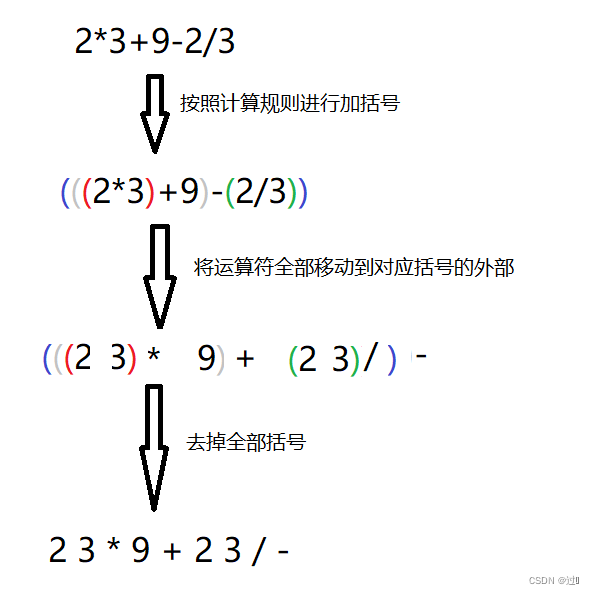
tokens,表示一个根据 逆波兰表示法 表示的算术表达式。逆波兰表达式也就是后缀表达式,我们通常使用的是中缀表达式,那么中缀表达式如何变成后缀表达式?
例如:
解题思路:由于本题给的就是一个后缀表达式,那么就不需要进行转换,可以通过遍历数组,如果是数字就入栈,如果是符号就弹出两个元素,分别作为左运算数和右运算数,因为-和/是要求运算顺序,然后将计算结果入栈,遍历完之后,栈中剩余的唯一元素就是表达式事务计算结果。
public int evalRPN(String[] tokens) {
Stack<String > stack=new Stack<>();
for(int i=0;i<tokens.length;i++){
if(tokens[i].equals("+")||tokens[i].equals("-")||tokens[i].equals("*")||tokens[i].equals("/")
&&!stack.isEmpty()){
int a=Integer.parseInt(stack.pop());
int b=Integer.parseInt(stack.pop());
int result=0;
switch(tokens[i]){
case "+":
result=b+a;
break;
case "-":
result=b-a;
break;
case "*":
result=b*a;
break;
case "/":
result=b/a;
break;
}
stack.push(String.valueOf(result));
}else{
stack.push(tokens[i]);
}
}
return Integer.parseInt(stack.pop());
}4、栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
解题思路:设置一个指针指向弹出序列的首个元素,将入栈序列的元素入栈,之后判断栈顶元素与指针所指的元素是否相同,若相同则指针后移,弹出栈顶元素,否则继续入栈,重复上述步骤,如果将入栈序列遍历完之后,栈不为空则返回false否则返回true。
public boolean IsPopOrder(int [] pushA,int [] popA) {
Stack<Integer> stack=new Stack<>();
int j=0;
for(int i=0;i<pushA.length;i++){
stack.push(pushA[i]);
while(!stack.isEmpty()&&j<popA.length&&stack.peek().equals(popA[j])){
stack.pop();
j++;
}
}
if(!stack.isEmpty()){
return false;
}
return true;
}5、最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。解题思路:在该问题中需要设置一个辅助栈minStack,
在插入元素时,如果minStack为空就直接插入,如果插入元素的值小于等于minStack的栈顶元素时就插入。
在删除栈顶元素时,如果minStack的栈顶元素与Stack的栈顶元素相同时也需要弹出。
在获取栈顶元素时,直接取Stack的栈顶元素。
在获取栈顶的最小元素时,则直接取minStack的栈顶元素。
class MinStack {
Stack<Integer> stack;
Stack<Integer> minStack;
public MinStack() {
stack=new Stack<>();
minStack=new Stack<>();
}
public void push(int val) {
stack.push(val);
if(minStack.isEmpty()){
minStack.push(val);
}else{
if(val<=minStack.peek()){
minStack.push(val);
}
}
}
public void pop() {
if(!stack.isEmpty()){
if(stack.pop().equals(minStack.peek())){
minStack.pop();
}
}
}
public int top() {
if(!stack.isEmpty()){
return stack.peek();
}
return -1;
}
public int getMin() {
return minStack.peek();
}
}