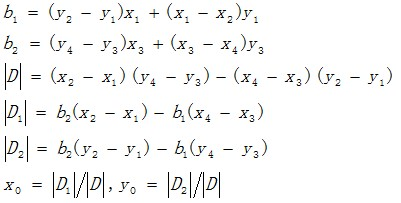美国人出的题真的难（个人感觉），看起来还行，做起来就是另外一会儿事儿了 

Farmer John's hobby of conducting high-energy physics experiments on weekends has backfired, causing N wormholes (2 <= N <= 12, N even) to materialize on his farm, each located at a distinct point on the 2D map of his farm (the x,y coordinates are both integers).
According to his calculations, Farmer John knows that his wormholes will form N/2 connected pairs. For example, if wormholes A and B are connected as a pair, then any object entering wormhole A will exit wormhole B moving in the same direction, and any object entering wormhole B will similarly exit from wormhole A moving in the same direction. This can have rather unpleasant consequences.
For example, suppose there are two paired wormholes A at (1,1) and B at (3,1), and that Bessie the cow starts from position (2,1) moving in the +x direction. Bessie will enter wormhole B [at (3,1)], exit from A [at (1,1)], then enter B again, and so on, getting trapped in an infinite cycle!
| . . . . | A > B . Bessie will travel to B then + . . . . A then across to B again
Farmer John knows the exact location of each wormhole on his farm. He knows that Bessie the cow always walks in the +x direction, although he does not remember where Bessie is currently located.
Please help Farmer John count the number of distinct pairings of the wormholes such that Bessie could possibly get trapped in an infinite cycle if she starts from an unlucky position. FJ doesn't know which wormhole pairs with any other wormhole, so \fBfind all the possibilities (i.e., all the different ways that N wormholes could be paired such that Bessie can, in some way, get in a cycle\fP). Note that a loop with a smaller number of wormholes might contribute a number of different sets of pairings to the total count as those wormholes that are not in the loop are paired in many different ways.
PROGRAM NAME: wormhole

INPUT FORMAT:

SAMPLE INPUT (file wormhole.in):
4 0 0 1 0 1 1 0 1
INPUT DETAILS:
There are 4 wormholes, forming the corners of a square.
OUTPUT FORMAT:

SAMPLE OUTPUT (file wormhole.out):
2
OUTPUT DETAILS:
If we number the wormholes 1..4 as we read them from the input, then if wormhole 1 pairs with wormhole 2 and wormhole 3 pairs with wormhole 4, Bessie can get stuck if she starts anywhere between (0,0) and (1,0) or between (0,1) and (1,1).
| . . d c . a b .
Here is a list of all the pairings, annotated with their wormhole results:
(a b) (c d) -- Bessie loops (a b) if she is on that line
(a c) (b d) -- Bessie loops b->d->c->a->b ... if she gets caught
(a d) (b c)
Only the pairings a-d and b-c allow Bessie to walk in the +x direction from any point in the 2D plane with no danger of cycling.

每日翻译（1/1）

题目大意：有n个虫洞，（n必为偶数），现在要将他分组，每两个虫洞一组，这两个虫洞无论进入哪一个都会被传送到另外一个虫洞，现要将n个虫洞分组，奶牛bessie从任意一点开始走，他只能向右走，问分组后将会陷入死循环的情况有几种

说实话蒟蒻翻译的太差了，画个图演示一下

 此时这两个黑洞配对，且小人现在在第一个黑洞。在这个时候他就会被传送到第二个黑洞

这下题目能看懂了吧

接下来其实就是搜索

第一步：枚举出所有配对情况

第二步：将所有配对情况一一考虑，并模拟是否会造成死循环。这里注意下，因为他只能向右走，所以只需要枚举纵坐标即可，也就是y轴

/*
ID:liusiyu3
TASK:wormhole
LANG:C++ 
*/
# include <iostream>
# include <cstdio>
# include <algorithm>
using namespace std;
# define int long long
int n,cnt;
struct node{
	int x;
	int y;
}a[15];
int b[15];
bool cmp(node a,node b){
	if (a.y==b.y){
		return a.x<b.x;
	}
	return a.y<b.y;
}
bool find_(int bushu,int now,int x,int way){//way=0表示目前是走路状态来到now点的，way=1表示目前是传送状态来到now点 
	if (now==x&&way==0&&bushu!=1){
		return true;
	}
	if (way==2){
		return find_(bushu+1,b[now],x,1);
	}else if (way==0){
		return find_(bushu+1,b[now],x,1);
	}else if (way==1){
		if (a[now].y==a[now+1].y){
			return find_(bushu+1,now+1,x,0);
		}else{
        	return 0;
		}
	}
}
bool check(){
	for (int i=1;i<=n;i++){
		if (find_(1,i,i,2)==true){
			return true;
		}
	} 
	return false;
}
void peidui(int x){
	if (x==n+1&&check()==true){
		cnt++;
		return;
	}
	if (b[x]==0){
        for (int i=x+1;i<=n;i++){
        	if (b[i]==0){
                b[i]=x;
				b[x]=i;
                peidui(x+1);
                b[i]=0;
				b[x]=0;
            }
		} 
    }
    if (b[x]!=0){
		peidui(x+1);
	}
	return ;
}
signed main(){
	freopen("wormhole.in","r",stdin);
	freopen("wormhole.out","w",stdout);
	scanf("%lld",&n);
	for (int i=1;i<=n;i++){
		scanf("%lld%lld",&a[i].x,&a[i].y);
	}
	sort(a+1,a+1+n,cmp);
	peidui(1);
	printf("%lld\n",cnt);
	fclose(stdin);
	fclose(stdout);
	return 0;
}