【排序4】探秘归并排序：提高程序效率的必备技巧

news2024/9/27 2:48:24

😊归并排序

🎊1、基本思想
🎊2、代码示例
🎊3、非递归实现
🎊4、归并排序的性能分析
🎊5、归并排序的优缺点
🎊6、归并排序的应用场景
🎊7、总结

🎊1、基本思想

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

🔍归并排序的实现可以分为两个主要步骤：分解和合并。
分解：将待排序序列平均分成两个子序列，递归地对子序列进行分解，直到子序列的长度为1（此时子序列已经有序）。
合并：将两个有序子序列合并成一个新的有序序列。合并操作从两个子序列的起始位置开始，比较两个子序列的当前元素，将较小的元素放入新序列中，并将该元素所在子序列的指针向后移动一位。重复此过程，直到一个子序列的所有元素都被放入新序列中。然后将另一个子序列的剩余元素依次放入新序列中。

合并如图：
在这里插入图片描述

🎊2、代码示例

public static void mergeSort(int[] array) {
        mergeFunc(array,0,array.length-1);
}

private static void mergeFunc(int[] array,int left,int right) {
	if(left >= right) {
		return;
    }
    int mid = left + ((right-left) >> 1);
    mergeFunc(array,left,mid);
    mergeFunc(array,mid+1,right);
    //左边分解完，右边分解完，开始合并
    merge(array,left,mid,right);
}

private static void merge(int[] array,int left,int mid,int right) {
	int s1 = left;
    int e1 = mid;
    int s2 = mid+1;
    int e2 = right;
    int[] tmpArr = new int[right-left+1];
    int k = 0;
    //1.保证两个表 都有数据
    while (s1 <= e1 && s2 <= e2) {
		if(array[s1] <= array[s2]) {
			tmpArr[k++] = array[s1++];
        }else {
            tmpArr[k++] = array[s2++];
        }
	}
	//2. 看哪个数组 还有数据 拷贝回去
    while (s1 <= e1) {
		tmpArr[k++] = array[s1++];
	}
    while (s2 <= e2) {
		tmpArr[k++] = array[s2++];
    }
    //3.拷贝到源数组
    for (int i = 0; i < k; i++) {
	}
}

🎊3、非递归实现

public static void mergeSortNor(int[] array) {
	int  gap = 1;
    //最外层循环 控制组数
    while (gap < array.length) {
		//每一组进行排序
        for (int i = 0; i < array.length; i = i+2*gap) {
        	int left = i;
        	int mid = left + gap-1;
        	if(mid >= array.length) {
			mid = array.length-1;
        	}
        	int right = mid+gap;
        	if(right >= array.length) {
        	right = array.length-1;
			}
        	merge(array,left,mid,right);
		}
		gap *= 2;
	}
}

🎊4、归并排序的性能分析

归并排序的时间复杂度为O(nlogn)，其中n为待排序序列的长度。这是因为归并排序每次都将序列分成两半，需要递归logn次。每次合并操作需要遍历所有元素，因此总的时间复杂度为O(nlogn)。归并排序的空间复杂度为O(n)，因为合并操作需要额外的空间来存储新序列。

🎊5、归并排序的优缺点

👻归并排序的优点包括：
1、稳定性：归并排序是一种稳定的排序算法，即相同元素的相对顺序在排序过程中不会改变。
2、时间复杂度：归并排序的时间复杂度为O(nlogn)，在处理大量数据时具有较高的性能。

🎉归并排序的缺点包括：
1、空间复杂度：归并排序的空间复杂度为O(n)，需要额外的空间来存储新序列。在内存受限的情况下，这可能会成为一个问题。

🎊6、归并排序的应用场景

归并排序在许多领域都有广泛的应用，例如：

1、外部排序：在处理大量数据且内存受限的情况下，归并排序是一种有效的外部排序算法。它可以将数据分成多个小块，分别排序后再合并。
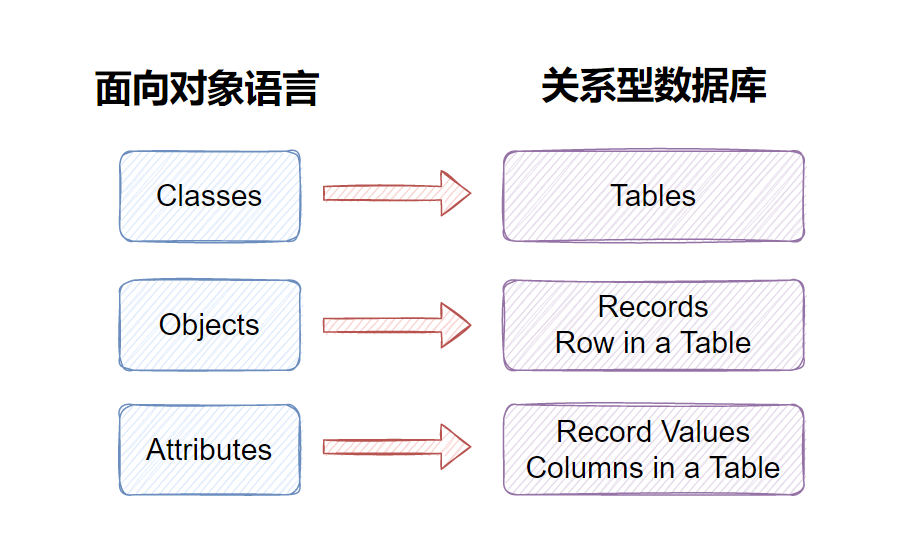
2、数据库系统：数据库系统在进行数据查询、排序和索引时，经常使用归并排序来提高性能。
3、大数据处理：在处理大规模数据集时，归并排序可以与其他算法（如MapReduce）结合使用，实现高效的数据处理和分析。