逻辑推理，形式逻辑：且关系，或关系，前加非后不变，箭头和或的转化

国考省考行测：逻辑推理，形式逻辑：且关系考点

2022找工作是学历、能力和运气的超强结合体!
公务员特招重点就是专业技能，附带行测和申论，而常规国考省考最重要的还是申论和行测，所以大家认真准备吧，我讲一起屡屡申论和行测的重要知识点
遇到寒冬，大厂不招人，可能很多算法学生都得去找开发，测开
测开的话，你就得学数据库，sql，oracle，尤其sql要学，当然，像很多金融企业、安全机构啥的，他们必须要用oracle数据库
这oracle比sql安全，强大多了，所以你需要学习，最重要的，你要是考网络警察公务员，这玩意你不会就别去报名了，耽误时间！
除了技术，申论和行测也得好好准备

文章目录

国考省考行测：逻辑推理，形式逻辑：且关系考点
@[TOC](文章目录)

考点2 且关系考察：联言命题，新闻联播：联合，都会播，且关系
定义
a且b，a与b同时成立
a且b且-c，仨同时成立

逻辑词
且、和、与，并列
递进词：更，而且，甚至
转折词：但，但是，却
语意并列，就是且关系，没有词引导

且关系的真假分析，考
当a，b全真时，则（a且b）为真
当a，b时有一个为假，则（a且b）为假
考察场景

或关系的考察，高难度，爱靠，相容选言问题
逻辑词
或关系的真假分析，重头戏
当ab有真时，a或b为真
当ab全假时，a或b为假

考试场景：箭头和或综合考察，贼难的
场景2：a或b，a假，则b必然真，-b——a真
题目是箭头多，或少，据此推理，思路：或变箭头
题目是有真有假，其中箭头无矛盾，且箭头的前或后有相同对象：箭头变或
或中推出关系的考察
真跟别的任意项或，都是真

要么关系：不相容选言命题
逻辑词
要么，要么，要么a，要么b，
ab有且只有一个成立/不成立

真假分析
使用场景
要么a，要么b，则a真b假，a假b真，b真a假，b假a真
要么与箭头的综合考场，考题可能考，很难的

且、或、要么的整体分析和综合考试

考点2 且关系考察：联言命题，新闻联播：联合，都会播，且关系

定义

a且b，a与b同时成立

a且b且-c，仨同时成立

在这里插入图片描述

逻辑词

且、和、与，并列

老章和老王是党员：章党员且王党员

递进词：更，而且，甚至

你进面了，而且是第一名，且

转折词：但，但是，却

你很丑但有钱，丑且有钱

语意并列，就是且关系，没有词引导

王是男博士，他爱吃糖，博士且爱吃糖
王是性感的男神，性感且男神
在这里插入图片描述
高富帅
矮肥黑
都是且关系
骚
不需要背诵
理解就行

且关系的真假分析，考

当a，b全真时，则（a且b）为真

全真则且真

当a，b时有一个为假，则（a且b）为假

有假则且关系为假
easy

好说
计算机中已经学烂了
在这里插入图片描述

考察场景

【1】与箭头综合考察
【2】单考真假分析，少

李班长，且王学委，上述为假，则下述哪个选项为真
反正有一个假就完事了
李不是班长，或王不是学委

-（a且b）=取反，符号取反，摩根等值定律==-a或-b
在这里插入图片描述
easy

在这里插入图片描述
理解就行

eg
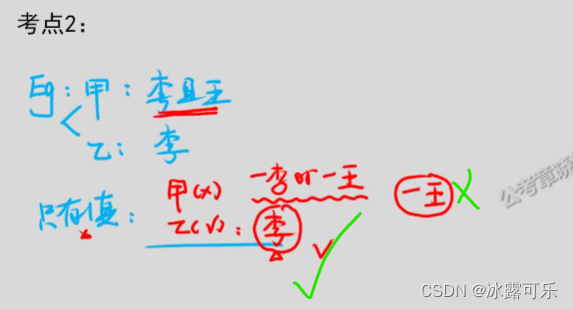
甲说：李是党员，且王是党员
乙说：李一定是党员
两者只有一个为真

不妨设甲真则李且王党员
那乙为假，李不是党员，矛盾了
所以甲不是真，甲为假
那就是-李或-王
此时，乙真，李是党员，则王不是党员，成立
故乙真

在这里插入图片描述

a——b且c且d
c不成立
请问能得出什么？
a一定不成立，因为bcd同时成立，c不成立，则a不可能成立
否后必否前

如果a且b——c且d
而-c
则
a且b为假
即-a或-b
正常
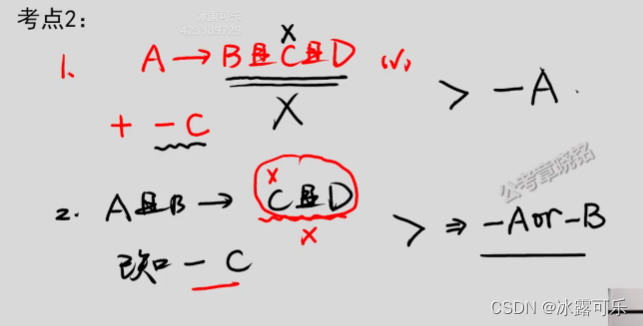
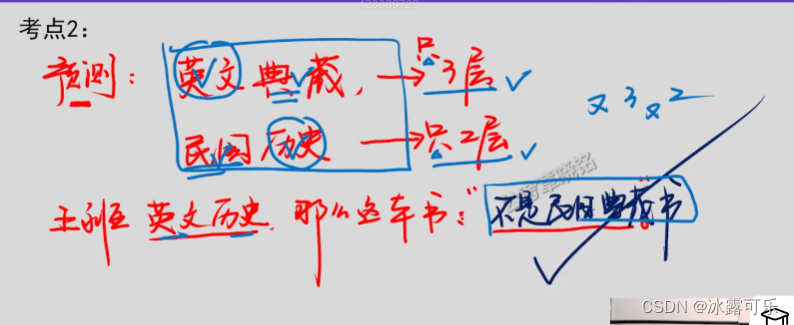
在这里插入图片描述
做预测
如果书是英文版典藏——只放在3层
如果书是民国历史——只放在2层
王，借了一本英文版的历史书，那么这书：
英文版且历史书——要么是典藏，要么是民国历史，但绝不可能是英文民国历史典藏

问：这书不是民国典藏书，对吗？对
因为英文，历史了，你如果是民国典藏，那不好意思，必须放23层，gg
在这里插入图片描述

a且b——c
d且e——-c
则c和-c不可能同时成立
如果abde都成立，则c和-c同时成立，矛盾
abde就绝不可能同时成立
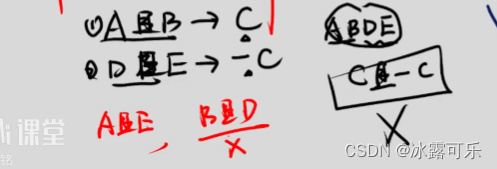
在这里插入图片描述

丽丽——强、装、铁且成立
否前后不定——不定
肯后前不定——不定
肯前必肯后——真
否后必否前——真
肯前否后——假

这个是箭头那边的规则
A肯前后不定，后面不知道的
B肯后前不定，前面不知道的
C肯前必肯后，后面多的真，C不对
D否后必否前，对的
在这里插入图片描述

或关系的考察，高难度，爱靠，相容选言问题

在这里插入图片描述
这个题很难，公考最爱靠
定义，几者中，至少一个成立，大于等于1个成立
abc至少一个成立，则a或b或c成立
a-b-c至少一个成立，a或-b或-c成立
有可能都成立
有真为真，全假为假
相容选言，就是可能都为真

李，王至少一个是lsp
可能俩都是lsp
有真为真，全假才假
在这里插入图片描述

逻辑词

a或b
a或者b
或a或b
或者a或者b
至少一个成立==或
不都不=至少一个=或
eg
a，b不都不是党员，-不都是党员，那么a至少有一个是
在这里插入图片描述

或关系的真假分析，重头戏

当ab有真时，a或b为真

至少一个成立，有真就行

当ab全假时，a或b为假

-至少一个，那么就是0个，一个都没有，全假
在这里插入图片描述

考试场景：箭头和或综合考察，贼难的

eg
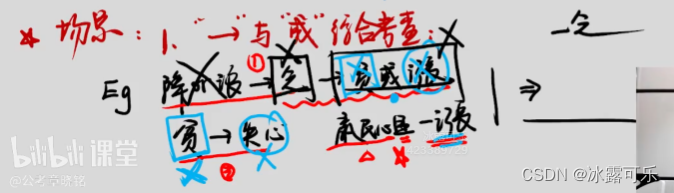
如果生产下降，或浪费严重，那么物资匮乏
如果物资匮乏，人民生活贫困，或物价暴涨
如果人民生活贫困，则政府失去民心
已知，政府赢得了民心，且物价没有暴涨，则：

赢得了民心且物价没有暴涨
赢得了民心——生活不贫困
加上物价没有暴涨，即**-（人民生活贫困，或物价暴涨）**==人民不贫困且物价没爆涨——物资不匮乏—— -（生产下降或浪费严重）
即生产上升了且没浪费
这就是结论
用逆否定律去做这个题
在这里插入图片描述

否前后不定——不定
肯后前不定——不定
肯前必肯后——真
否后必否前——真
肯前否后——假
记住哦
单独肯前，肯后，其余都不定
否后必然要否前
肯前必然要肯后——真的
如果肯前且否后了——假的

这些规则要牢记，结合或关系考试，就是公考经常考的题目

场景2：a或b，a假，则b必然真，-b——a真

这仨等价关系，这点很重要
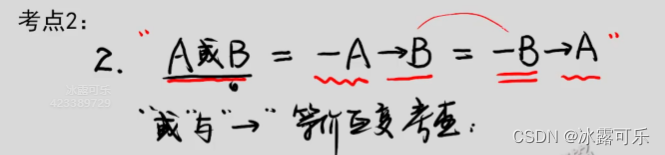
在这里插入图片描述

摩根等值
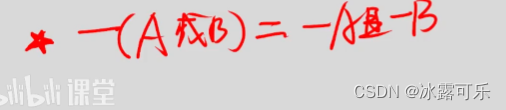
在这里插入图片描述
a或b==-a——b，鲁滨逊定律，否定肯定式

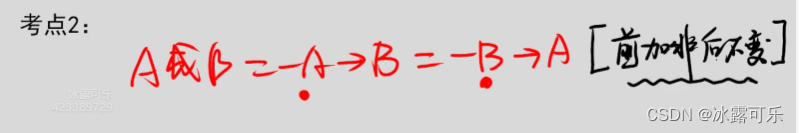
eg甲：李，王都是党员
乙：李是党员
若只有一个人真话，则：
如果甲是真，则乙必然假，李不是党员，甲又说李是党员，矛盾了
若果甲是假，则乙必然真，-（李且王）=-李或-王，而乙那说了李是党员那-王必然是真
所以王不是党员
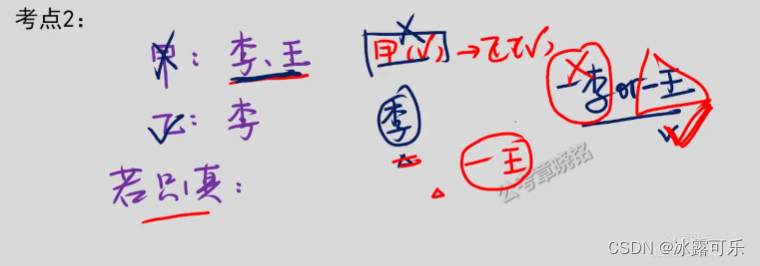
在这里插入图片描述
这就是a或b，则-a——b

题目是箭头多，或少，据此推理，思路：或变箭头

在这里插入图片描述

eg
甲：如果吃海带，就要吃豆包：海——豆
乙：除非吃藕片，否则不吃鸭血：-藕—— -鸭
丙：或不吃豆包，或不吃藕片：-豆或-藕
据此可以得出：

箭头多，或者少：或变箭头**【转换原则，是前加非，后不变】**
豆—— -藕
就是吃豆包，必然不吃藕片
则
海——豆—— -藕—— -鸭
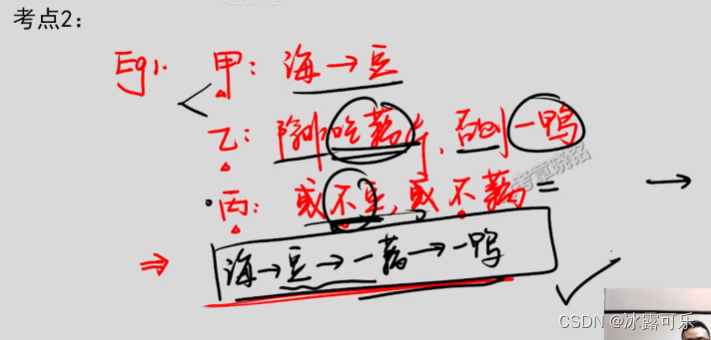
在这里插入图片描述
箭头关系已经建立起来了
则，再用我们的真假规则来判断选项

肯前后不定，肯后前不定——不定
肯前必肯后，否后必否前——真
肯前必否后——假

知道这种题目怎么做了吗？?
就这意思

题目是有真有假，其中箭头无矛盾，且箭头的前或后有相同对象：箭头变或

在这里插入图片描述
eg
甲：李是党员——王是党员
乙：只有章不是党员，李才是党员
丙：郑是党员但刘不是党员
以上仨只有1个真，据此：

绝对不能带入abcd答案，都没法判断！！！！！！！！！！！！！！！！！

所以，必须要建立箭头，然后判断真假
画箭头：
李党员——王是党员
李党员——章不是党员
郑党员且刘-党员

因为甲乙是箭头，且箭头的左边都是李，同一个对象
这时候必须把箭头转换为或关系 【转换原则，就是前加非，后不变】
李-党员或王是党员
李-党员或章-党员
郑党员且刘-党员

如果李-党员，则前面2项都是真，违背了：以上仨只有1个真
所以李是党员
在这里插入图片描述
这种题真牛逼！！！！！！！！
难，但是技巧就是上面的规则
牛逼
牛逼

a——b
a——c
两者只有一真
那么马上转换为或关系
-a或b
-a或c
两者只有一真，则-a一定是假
a一定是真
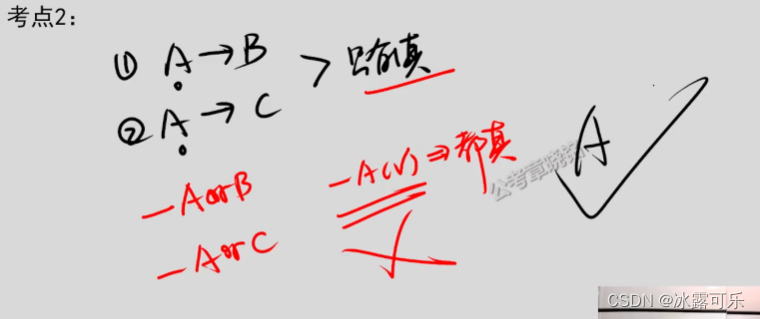
在这里插入图片描述
这就是箭头转换为或关系的骚操作

这就是箭头和或关系的2个原则了
【箭头太多，或很少，则或变箭头，原则：前加非，后不变】
【箭头无矛盾，且箭头的前或后都有同样的对象，则箭头变或，原则：前加非，后不变】

eg
若果办画展，一定办书展
如果不办诗歌，则要办书展
办舞蹈，且不办艺术展
仨只有一真，则
画——书
-诗歌——书
办舞蹈且-办艺术展
箭头没有矛盾，后面都是办书展，则将箭头变或**【原则就是前加非后不变】**
-画或书
诗歌或书
办舞蹈且-办艺术展
由于上述仨只有一个真，故书决不能为真，否则12都是真，违背了原则
故，-书
一定不办书展
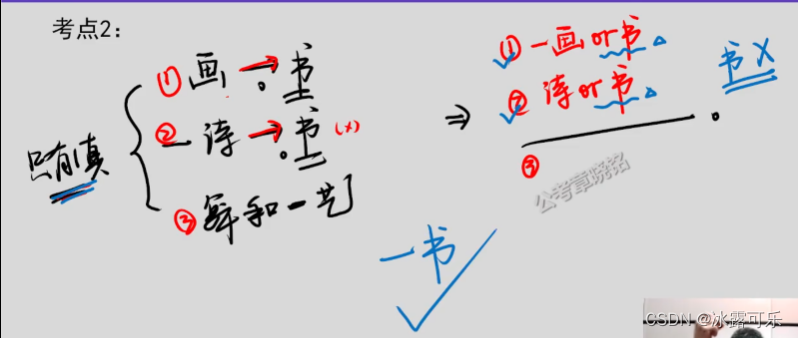
在这里插入图片描述
懂了吗？

在这里插入图片描述
你这个题因为箭头和或一样多，而且前后可能矛盾
所以上面的规则用不了
只能先把箭头写出来
然后带入选项
发现，D，苏老师不教物理，则4中吴老师必然教化学
2中或后面就不对，则前面必然对，就是孙老师一定教语文
懂？
D对了

或中推出关系的考察

真跟别的任意项或，都是真

在这里插入图片描述

如果仨只有一真，则，甲不真
因为甲真，则甲或别的必然真，2就成立了，违背了仨只有一真的原则

eg
王：选2个队长，华且果
章：华和果至少有一个参加
先：上述有一个为真，则先认为：
不妨设王真：则华且果——华或果
那章也真，违背了先的一个真原则
那就是章是对的
-华或-果
华和果至少一个选
选且只选1个
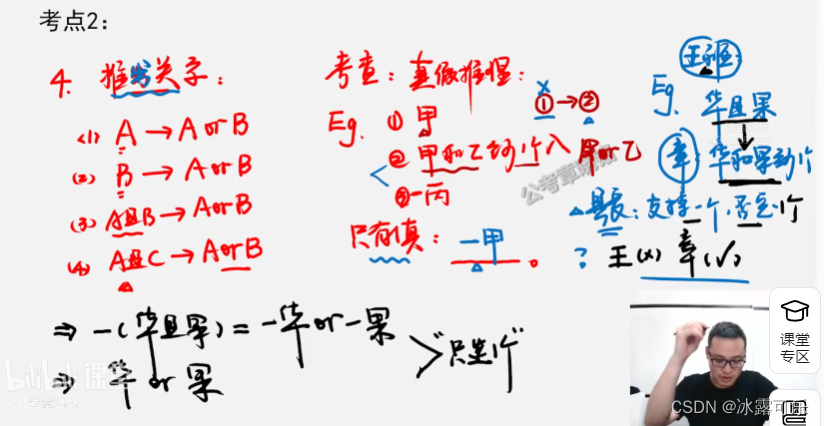
在这里插入图片描述
要么选华，要么选果
a且c，a必然

eg
王：选章和郑
狗：选章或张
已知，2只有一真，则

章和郑如果为真——章或张必然成立
所以-（章和郑）=-章或-郑
狗对的
后续其他的不懂了就
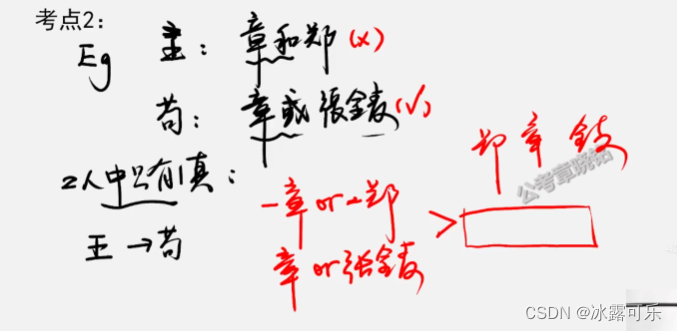
在这里插入图片描述

要么关系：不相容选言命题

或：相容
定义：两者中有且仅有一个成立
a和b有且只有一个成立，a要么a，要么b
这次公考，要么考上，要么落榜
要么生，要么死
不相容，二选择一
在这里插入图片描述

逻辑词

要么，要么，要么a，要么b，

ab有且只有一个成立/不成立

在这里插入图片描述

真假分析

当ab一真一假的时候，则要么a，要么b为真
全真或全假时，要么a要么b为假

一真一假为真，全真全假为假
在这里插入图片描述

使用场景

要么a，要么b，则a真b假，a假b真，b真a假，b假a真

在这里插入图片描述

要么与箭头的综合考场，考题可能考，很难的

eg
-考上的人，要么没上上岸存，要么没做题
如果真，据此可以推出：
a：考上的人，一定报了上岸存且做题了
b：报了上岸存，且做题了，一定考上了
c：报了上岸存，考上了
d：做题的人，一定没考上
e：既没有报上岸存，又没有做题，一定考不上

否前后不定
肯后前不定
肯前必肯后，否后必否前——真
肯前否后——假

-考上的人——要么没上上岸存，要么没做题
a：
否前后不定，所以a不对，谁知道呢？
b
报了，还做了题，，对于要么来说：全假，则后面为假，否后必否前，它考上了，没错
c
报了上岸存，对于要么来说：没说做没做题，无法搞出一真一假为真，所以c不知道啊
d
做了题，对于要么来说：没说是否报上岸村，无法搞出一真一假为真，所以d不知道啊
e
没报，没做题，，对于要么来说：全真全假为假，所以否后必否前，它一定考上，e对的

这的关键是判定要么要么整体是真还是假
一真一假为真
全真全假为假

否前后不定，肯后前不定
否后必否前，肯前必肯后——真
肯前否后——假
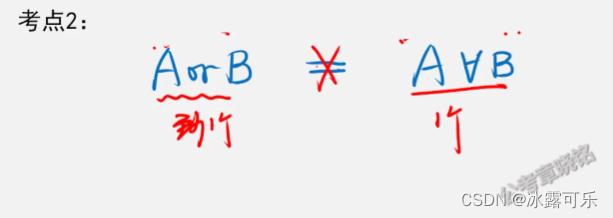
在这里插入图片描述
或跟要么要么是不等价的
或的推出关系就多了一个
要么要么，有且只有一个成立，则能推出或关系

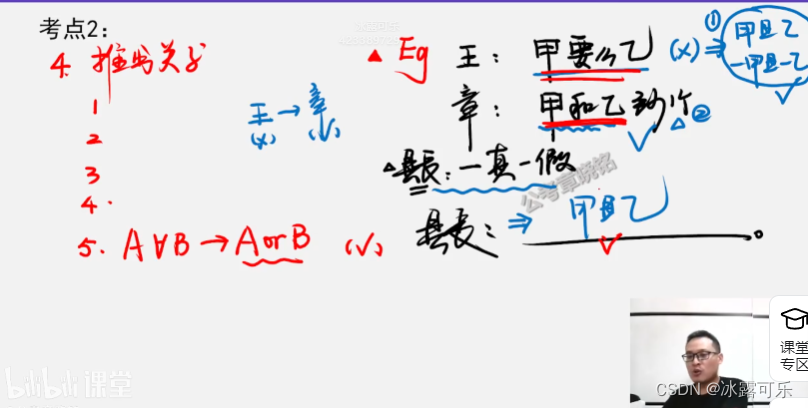
在这里插入图片描述
eg
王：甲要么乙去锻炼
章：甲，乙至少有一个去锻炼
县长：上述2只有一真
甲和乙二选一
甲或乙去
王能推出章，所以都成立，那跟县长违背了
所以王是错的，章是真的
-（甲，要么乙）
也就是说全真，全假才能让整体假
全假的话，甲乙都不去，而章至少有一个，那不行
因此，甲乙都得去
这样的话，满足王假，章真