读AI3.0笔记07_游戏与推理
news2026/2/14 21:17:09
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1411682.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
引领未来:云原生在产品、架构与商业模式中的创新与应用
文章目录 一、云原生产品创新二、云原生架构设计三、云原生商业模式变革《云原生落地 产品、架构与商业模式》适读人群编辑推荐内容简介目录 随着云计算技术的不断发展,云原生已经成为企业数字化转型的重要方向。接下来将从产品、架构和商业模式三个方面,…
融合创新:传统企业数字化转型的业务、战略、操作和文化变革
引言
随着科技的不断演进,传统企业正站在数字化转型的前沿,这是一场前所未有的全面变革之旅。数字化已经超越了单纯的技术升级,成为企业保持竞争力、开创未来的必然选择。本文将引领您探讨,迈向数字化未来的传统企业全面数字化转…
回归预测 | Matlab基于SSA-SVR麻雀算法优化支持向量机的数据多输入单输出回归预测
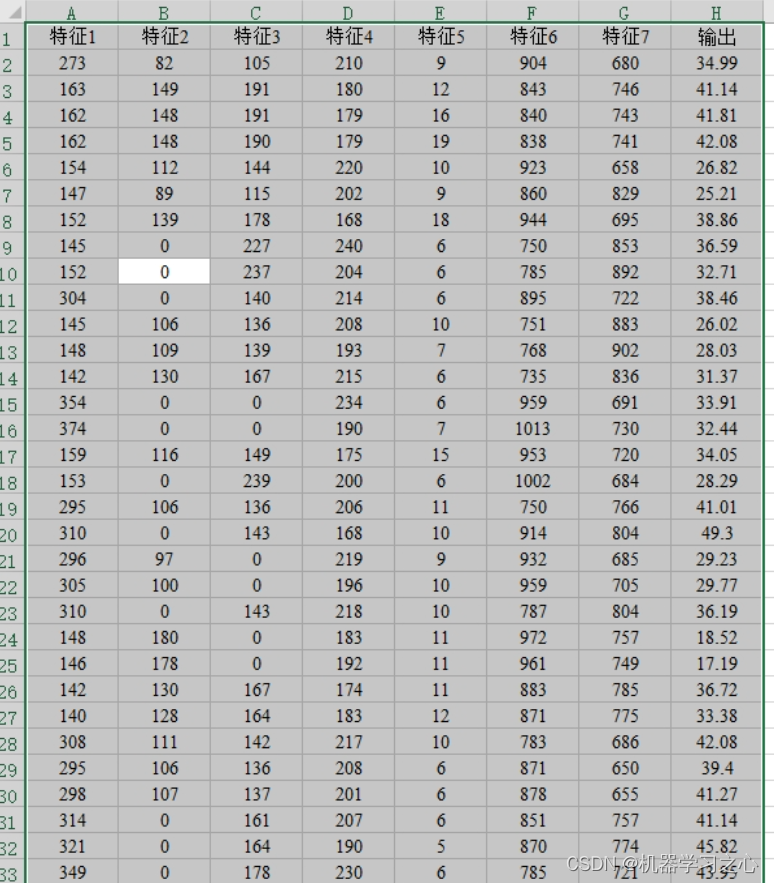
回归预测 | Matlab基于SSA-SVR麻雀算法优化支持向量机的数据多输入单输出回归预测 目录 回归预测 | Matlab基于SSA-SVR麻雀算法优化支持向量机的数据多输入单输出回归预测预测效果基本描述程序设计参考资料 预测效果 基本描述 1.Matlab基于SSA-SVR麻雀算法优化支持向量机的数据…
解密:消息中间件的选择与使用:打造高效通信枢纽
目录
第一章:消息中间件介绍
1.1 什么是消息中间件
1.2 消息中间件的作用
1.3 消息中间件的分类
第二章:消息中间件的选择标准
2.1 性能
2.2 可靠性
2.3 可扩展性
2.4 易用性
2.5 社区支持
2.6 成本
第三章:常见的消息中间件对比…
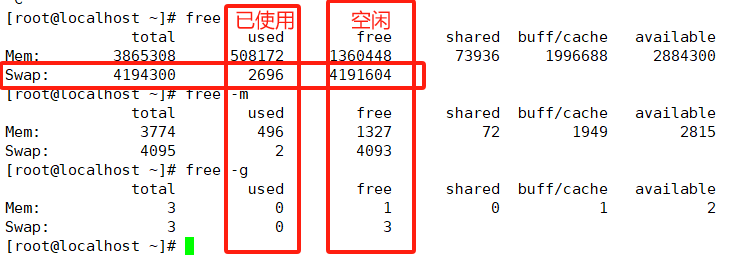
docker 网络及如何资源(CPU/内存/磁盘)控制
安装Docker时,它会自动创建三个网络,bridge(创建容器默认连接到此网络)、 none 、host
docker网络模式
Host
容器与宿主机共享网络namespace,即容器和宿主机使用同一个IP、端口范围(容器与宿主机或其他使…
[ACM学习] 进制转换
进制的本质
本质是每一位的数位上的数字乘上这一位的权重 将任意进制转换为十进制 原来还很疑惑为什么从高位开始,原来从高位开始的,可以被滚动地乘很多遍。
将十进制转换为任意进制
VsCode提高生产力的插件推荐-持续更新中
别名路径跳转
自定义配置// 文件名别名跳转
"alias-skip.mappings": {
"~/": "/src",
"views": "/src/views",
"assets": "/src/assets",
"network": "/src/network",
"comm…
Supervised Contrastive 损失函数详解
有什么不对的及时指出,共同学习进步。(●’◡’●)
有监督对比学习将自监督批量对比方法扩展到完全监督设置,能够有效地利用标签信息。属于同一类的点簇在嵌入空间中被拉到一起,同时将来自不同类的样本簇推开。这种损失显示出对自然损坏很稳…
支付宝AES如何加密
继之前给大家介绍了 V3 加密解密的方法之后,今天给大家介绍下支付宝的 AES 加密。 注意:以下说明均在使用支付宝 SDK 集成的基础上,未使用支付宝 SDK 的小伙伴要使用的话老老实实从 AES 加密原理开始研究吧。 什么是AES密钥
AES 是一种高级加…
虚幻UE 插件-像素流送实现和优化
本笔记记录了像素流送插件的实现和优化过程。 UE version:5.3 文章目录 一、像素流送二、实现步骤1、开启像素流送插件2、设置参数3、打包程序4、打包后的程序进行像素流参数设置5、下载NodeJS6、下载信令服务器7、对信令服务器进行设置8、启动像素流送 三、优化1、…
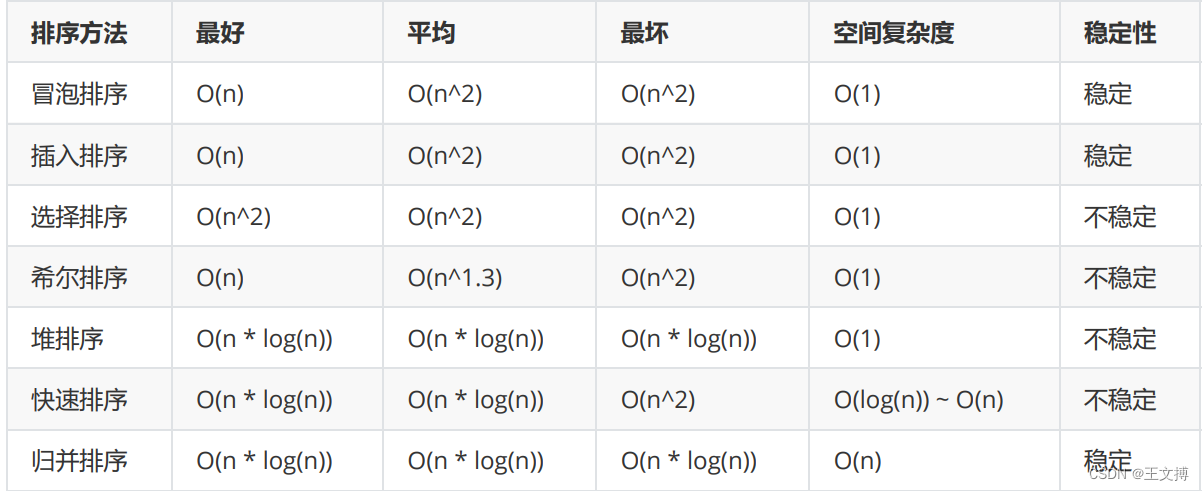
数据结构排序算详解(动态图+代码描述)
目录 1、直接插入排序(升序)
2、希尔排序(升序)
3、选择排序(升序)
方式一(一个指针)
方式二(两个指针)
4、堆排序(升序) 5、冒…
精酿啤酒:啤酒花的选择与处理方法
啤酒花在啤酒的酿造过程中起着重要的作用,它不仅赋予啤酒与众不同的苦味和香味,还为啤酒的稳定性提供了帮助。对于Fendi Club啤酒来说,啤酒花的选择和处理方法更是重要。下面,我们将深入探讨Fendi Club啤酒在啤酒花的选择和处理方…
一文详解C++拷贝构造函数
文章目录 引入一、什么是拷贝构造函数?二、什么情况下使用拷贝构造函数?三、使用拷贝构造函数需要注意什么?四、深拷贝和浅拷贝浅拷贝深拷贝 引入
在现实生活中,可能存在一个与你一样的自己,我们称其为双胞胎。 相当…
【并发编程】 synchronized的普通方法,静态方法,锁对象,锁升级过程,可重入锁,非公平锁
目录 1.普通方法
2.静态方法
3.锁对象
4.锁升级过程
5.可重入的锁
6.不公平锁
非公平锁的 lock 方法: 1.普通方法 将synchronized修饰在普通同步方法,那么该锁的作用域是在当前实例对象范围内,也就是说对于 SyncDemosdnewSyncDemo();这一个实例对象…
el-table 动态渲染多级表头;一级表头根据数据动态生成,二级表头固定
一、表格需求:
实现一个动态表头,一级表头,根据数据动态生成,二级表头固定,每列的数据不一样,难点在于数据的处理。做这种表头需要两组数据,一组数据是实现表头的,另一组数据是内容…
【洛谷】P1135奇怪的电梯(DFS)
这题利用 dfs 解决,编程实现比较简单。
具体来说,每层楼有两种可能,上楼或下楼,因此可以形成一个以 a 楼为根的二叉树,因此只需一个 for 循环遍历某个父节点的两个子节点,之后递归就行。
易错点ÿ…
马尔可夫预测(Python)
马尔科夫链(Markov Chains)
从一个例子入手:假设某餐厅有A,B,C三种套餐供应,每天只会是这三种中的一种,而具体是哪一种,仅取决于昨天供应的哪一种,换言之&#…


![[ACM学习] 进制转换](https://img-blog.csdnimg.cn/direct/e20f57219fba4eb6a23e04e0657d81fc.png)