目录

1、直接插入排序（升序）

2、希尔排序（升序） 

3、选择排序（升序）

方式一（一个指针）

方式二（两个指针）

4、堆排序（升序）

 5、冒泡排序（升序）

6、快速排序 （升序）

方式一（Hoare方法）

方式二（挖坑法） 

 快排改进算法（三数取中）

7、归并排序

8、总结

---

1、直接插入排序（升序）

描述：对于一个数组i从第二个数据开始比较，j=i-1，j<0停止，每次i下标元素放到临时变量tmp中与j下标比较，如果大于j下标，tmp还放回原位置，i和j都加加，如果小于j下标，j--,直到找到大于j下标元素，tmp放到j+1下标

时间复杂度：最好情况下O(n),最坏情况O(n^2)

空间复杂度：O（1）

//直接插入排序
//时间复杂度：最好情况下O(n),最坏情况O(n^2)
public class Test1 {
    public static void sort(int []array){
        for (int i = 1; i <array.length ; i++) {
            int tmp=array[i];
            int j = i-1;
            for (; j >=0 ; j--) {
                if(tmp<array[j])
                    array[j+1]=array[j];
                else break;
            }
            array[j+1]=tmp;
        }
    }
}

2、希尔排序（升序） 

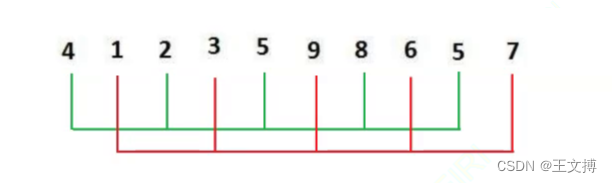
描述：我们先对数组中数据分组，数组长度即位N,具体先分为gap组，gap=N/2,N/4,N/8.....1。然后对每一组直接插入排序。

时间复杂度：O(n*log2（N)）,空间复杂度：O（1）

每种颜色一组例如：

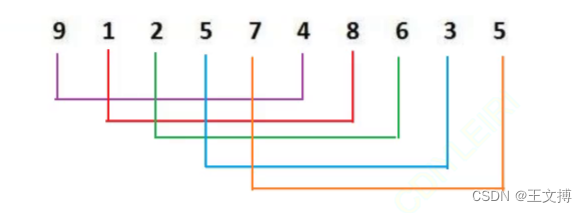
例如：

public static void ShellSort(int [] array){
        int gap=array.length;//10
        while (gap>1){
            gap=gap/2;
            Sort(array,gap);//5,2,1
        }
    }
    private static void Sort(int [] array,int gap){
        for (int i = gap; i <array.length ; i++) {
            int tmp=array[i];
            int j = i-gap;
             //每组直接插入排序
            for (; j >=0 ; j=j-gap) {
                if (tmp<array[j])array[j+gap]=array[j];
                else break;
            }
            array[j+gap]=tmp;
        }

3、选择排序（升序）

方式一（一个指针）

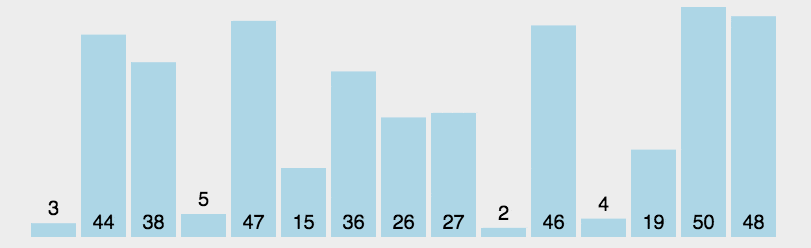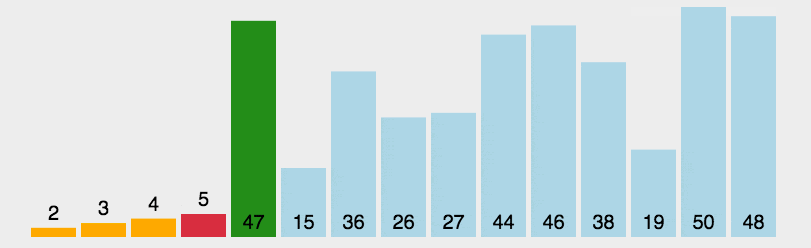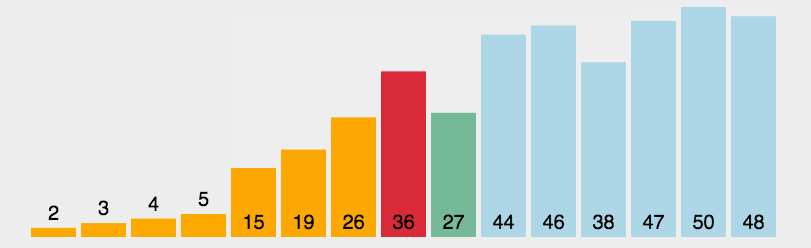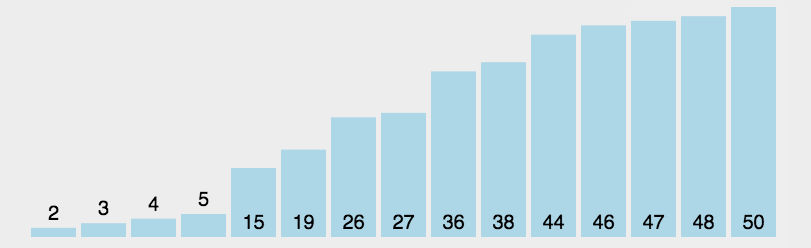
描述： 每次找最小值下标，与i下标交换，i++

空间复杂度：O（1），时间复杂度：O(N^2)

 public static void selcetSort(int [] array){
        for (int i = 0; i <array.length ; i++) {
            int min=i;//记录每次最小值下标
            for (int j = i+1; j <array.length ; j++)
                if (array[j]<array[min])min=j;
            swap(min,i,array);
        }
    }
 private static void swap(int i ,int j,int [] array){
        int tmp=array[i];
        array[i]=array[j];
        array[j]=tmp;
    }

方式二（两个指针）

思路：left,right指向数组的两端，每次遍历找到最大值和最小值，分别赋值给lefgt和right

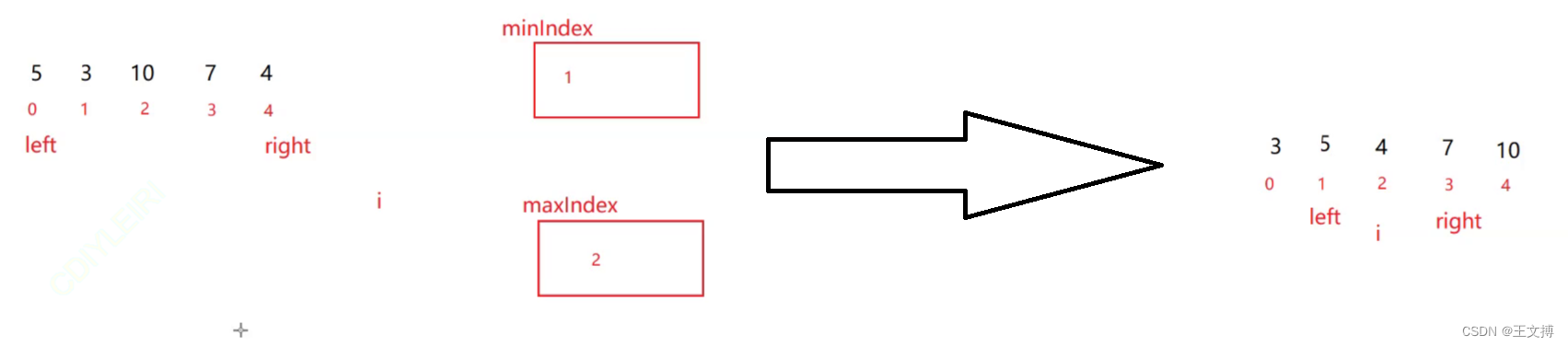
 public static void selectSort2(int[] array) {
        int left = 0;
        int right = array.length-1;
        int i;
        while (left < right) {
        //i  minIndex   maxIndex
            int minIndex=left,maxIndex=right;
            i=left+1;
            for(;i<right;i++){
                if (array[i]<=array[minIndex])minIndex=i;
                if (array[i]>array[maxIndex])maxIndex=i;
            }
            swap(left,minIndex,array);
            swap(right,maxIndex,array);
            left++;
            right--;
        }
    }
    private static void swap(int i ,int j,int [] array){
        int tmp=array[i];
        array[i]=array[j];
        array[j]=tmp;
    }

4、堆排序（升序）

思路：先创建成大根堆，每次排序把根节点与最后位置元素交换后向下调整，下一次根节点与end-1下标交换后向下调整，直到end<0;结束

 public static void HeapSort(int[]array){
        creatHeap(array.length,array);//创建大根堆
        int end=array.length-1;
        while (end>0){
            swap(end,0,array);
            signHeap(0,end,array);//向下调整不挑最后一个所以后减减
            end--;
        }

    }
    public static void creatHeap(int end,int [] array){
        int preheap;//每次的根节点
        for ( preheap=(end-1-1)/2;preheap>=0;preheap--){
            signHeap(preheap,end, array);
        }

    }
    //向下调整为大根堆为例
    private static void signHeap(int preheap,int end,int [] array){//向下调整
        int child=preheap*2+1;//preheap左子树下标
        while (child<end){
            if(child+1<end&&array[child]<array[child+1])child++;
            //现在child指向孩子节点的最大值
            if (array[preheap]<array[child]){
                swap(preheap,child,array);
                preheap=child;
                child=child*2+1;
            }
            else break;
        }
    }
    private static void swap(int i ,int j,int [] array){
        int tmp=array[i];
        array[i]=array[j];
        array[j]=tmp;
    }

 5、冒泡排序（升序）

 

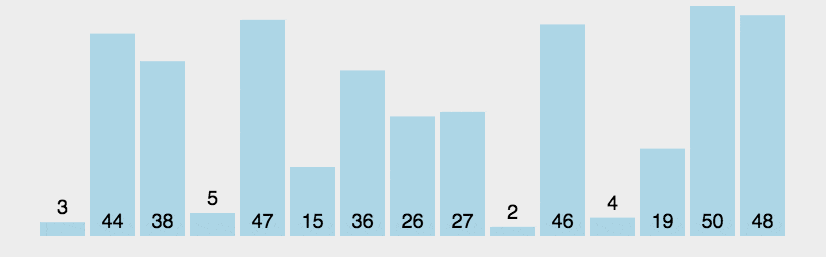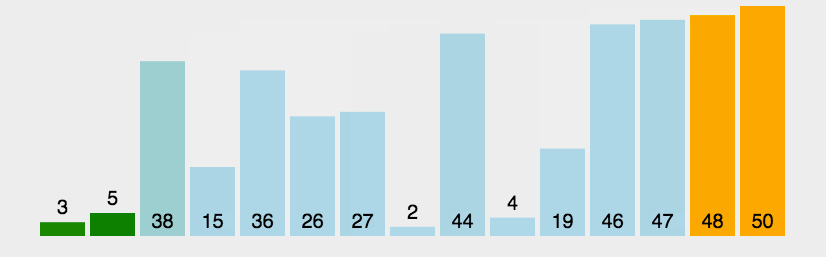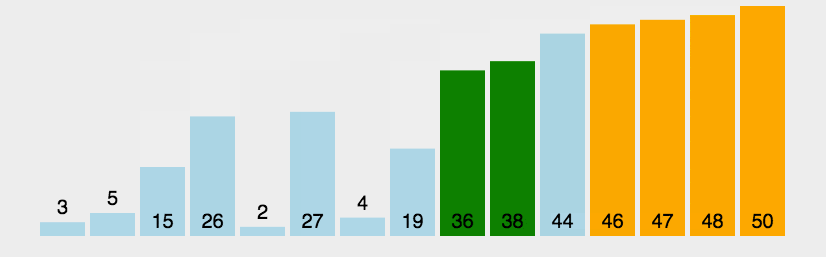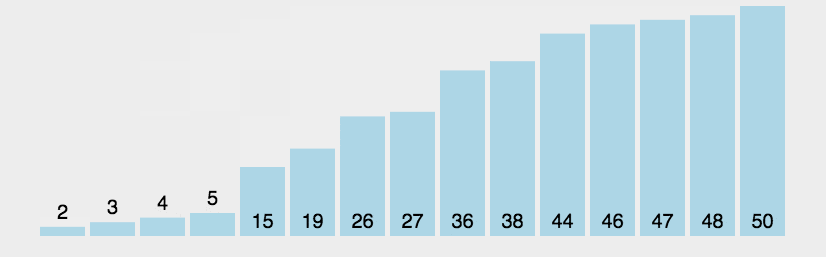
时间复杂度:O(N^2),空间复杂度O(1)

 public static void bubbleSort(int [] array){
        for (int i = 0; i < array.length-1; i++) {
            boolean flag=false;
            for (int j = 0; j < array.length-1; j++) {
                if (array[j]>array[j+1]){
                    swap(j,j+1,array);
                    flag=true;
                }
            }
            if (flag==false)break;
        }
    }
    private static void swap(int i ,int j,int [] array){
        int tmp=array[i];
        array[i]=array[j];
        array[j]=tmp;
    }

6、快速排序 （升序）

方式一（Hoare方法）

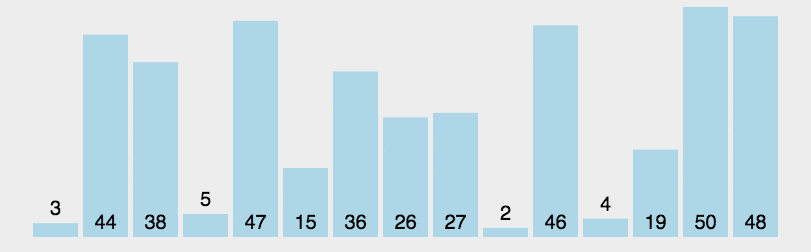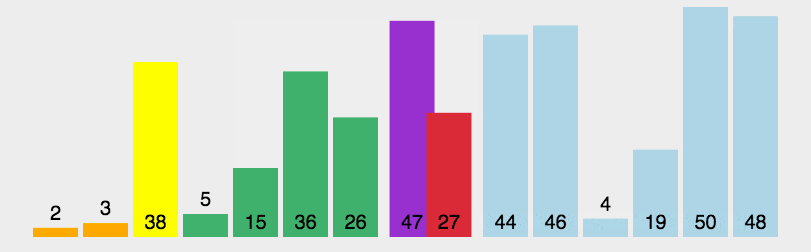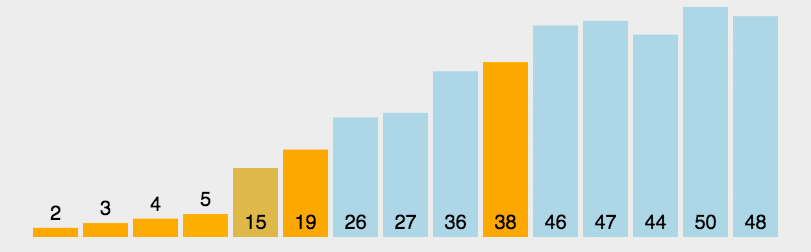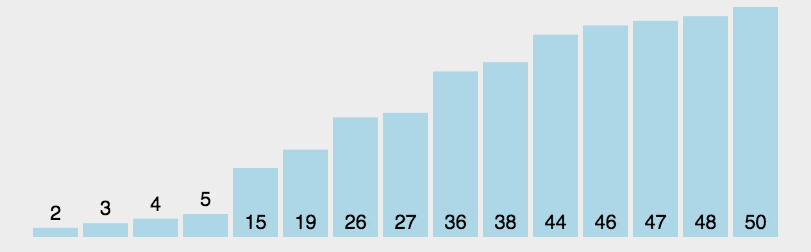
描述： 

每次都是最左边的元素是基点，从左边往右找到比基点大的跟从右往左找到比基点小的交换，最后left和right交点和基点交换，这样排完一次后交点左边比交点值小，后边大，分左右递归在排

时间复杂度:O(Nlog2(N)),空间复杂度O(log2(N))

    public static void quick(int [] array){
        int start=0,end=array.length-1;
        quickSort(array,start,end);
    }
    private static void quickSort(int [] array,int start,int end){
        if(start>=end)return;
        int mid=sort(array,start,end);
        quickSort(array,start,mid-1);
        quickSort(array,mid+1,end);
    }
    private static int sort(int [] array,int left,int right){
        int tmp=array[left];//基准
        int i=left;
        //先写右的right--，否则一遍走到left==right后与i下标交换的那一次且仅仅一次将会不有序
        while (left<right) {
            while (left < right && tmp <=array[right]) right--;//找到比tmp小的数
            while (left < right && tmp >= array[left]) left++;//找到比tmp大的数
            swap(right, left, array);
        }
        swap(left,i,array);
        return left;//left==right==mid
    }
    private static void swap(int i ,int j,int [] array){
        int tmp=array[i];
        array[i]=array[j];
        array[j]=tmp;
    }

方式二（挖坑法） 

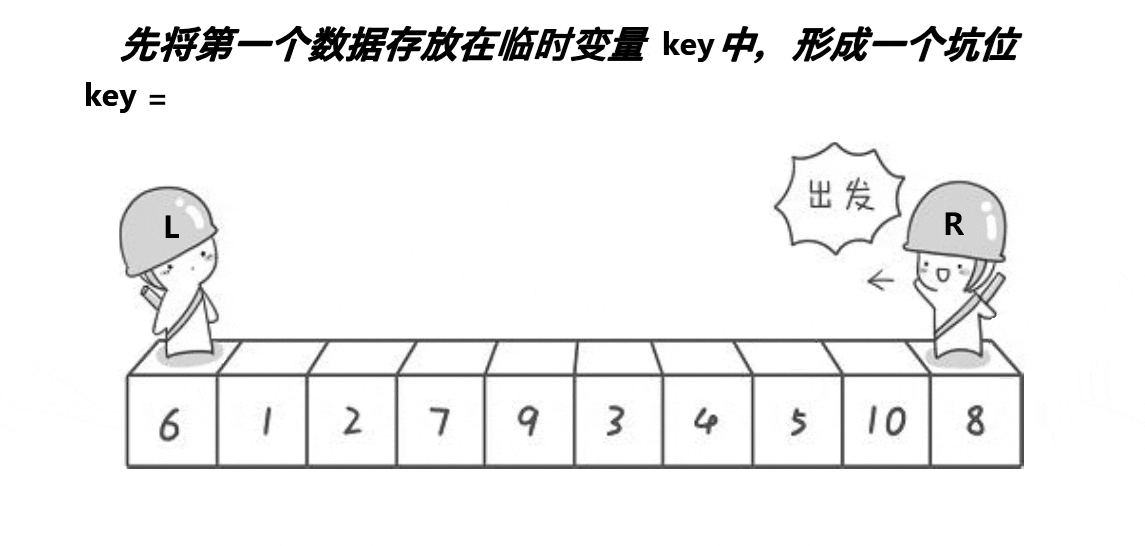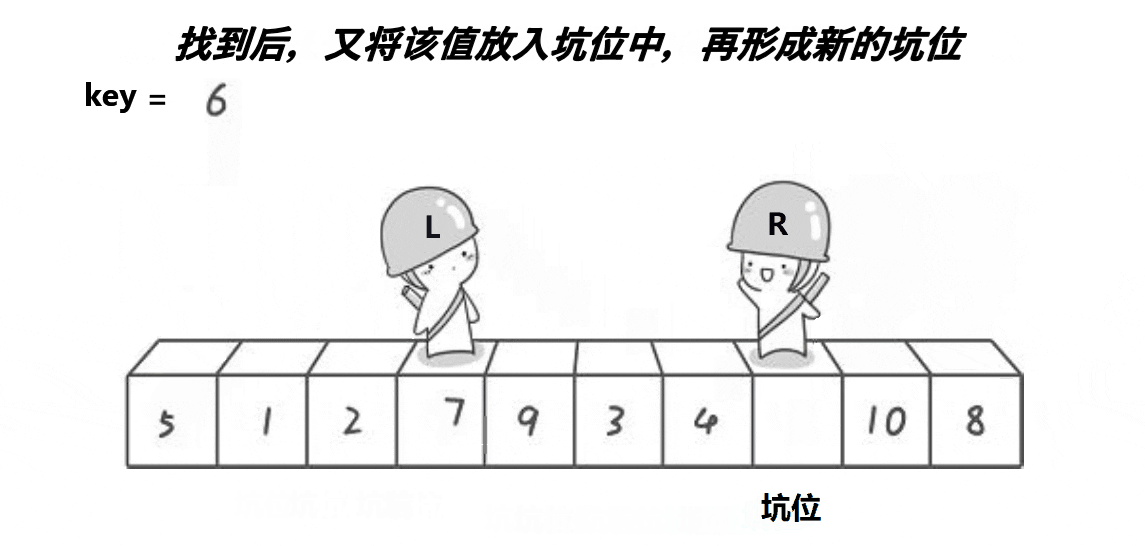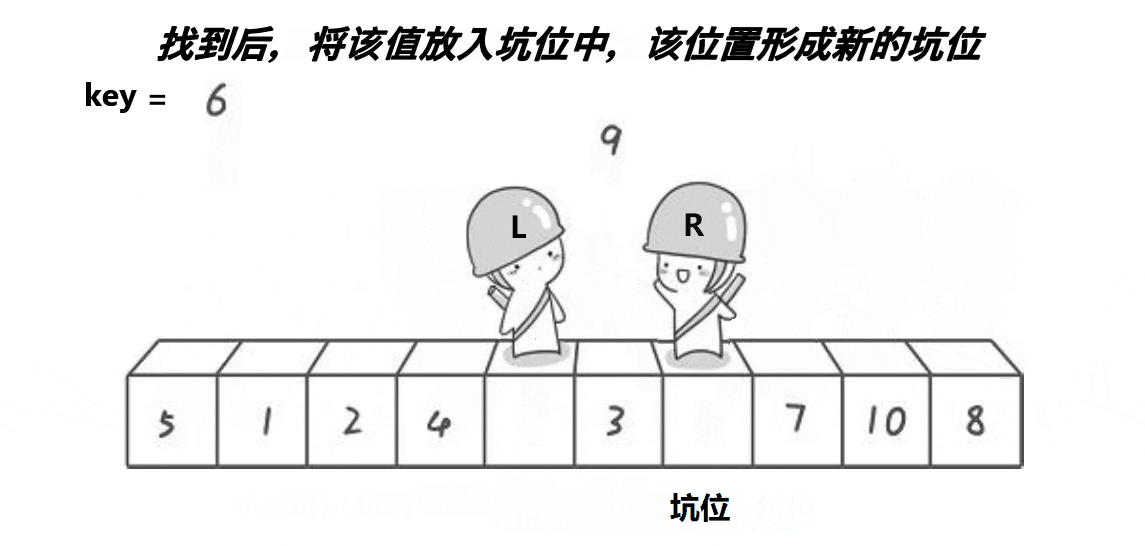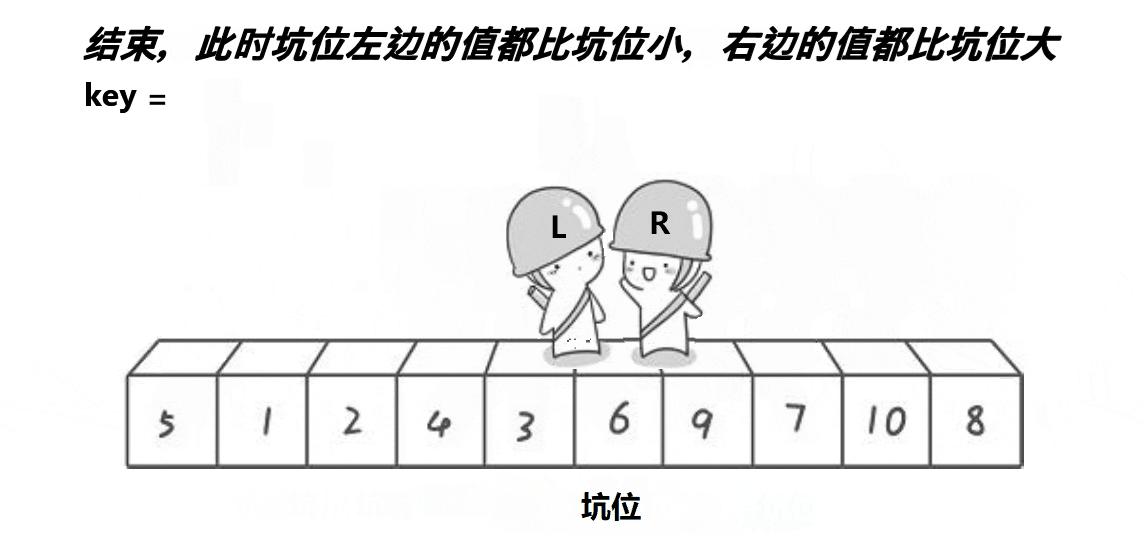
 思想：每次都是最左边的元素是基点，保存基点下标，此处就是一个坑，从右往左找到比基点小的放到基点下标，放到坑处 ，刚从右边放过来的元素位置就有是一个新的坑，我们再从左往右找到比基点大的元素放到新坑，当然这里又是一个坑。。。

时间复杂度:O(Nlog2(N)),空间复杂度O(log2(N))

    public static void quick(int [] array){
        int start=0,end=array.length-1;
        quickSort(array,start,end);
    }
    private static void quickSort(int [] array,int start,int end){
        if(start>=end)return;
        int mid=sort(array,start,end);
        quickSort(array,start,mid-1);
        quickSort(array,mid+1,end);
    }
    private static int sort(int [] array,int left,int right){
        int tmp=array[left];//基准
        int i=left;
        //先写右的right--，否则一遍走到left==right后与i下标交换后的那一次将会不有序
        while (left<right) {
            while (left < right && tmp <=array[right]) right--;//找到比tmp小的数
            array[left]=array[right];
            while (left < right && tmp >= array[left]) left++;//找到比tmp大的数
            array[right]=array[left];
        }
        array[left]=tmp;//最后入坑
        return left;//left==right==mid
    }

 快排改进算法（三数取中）

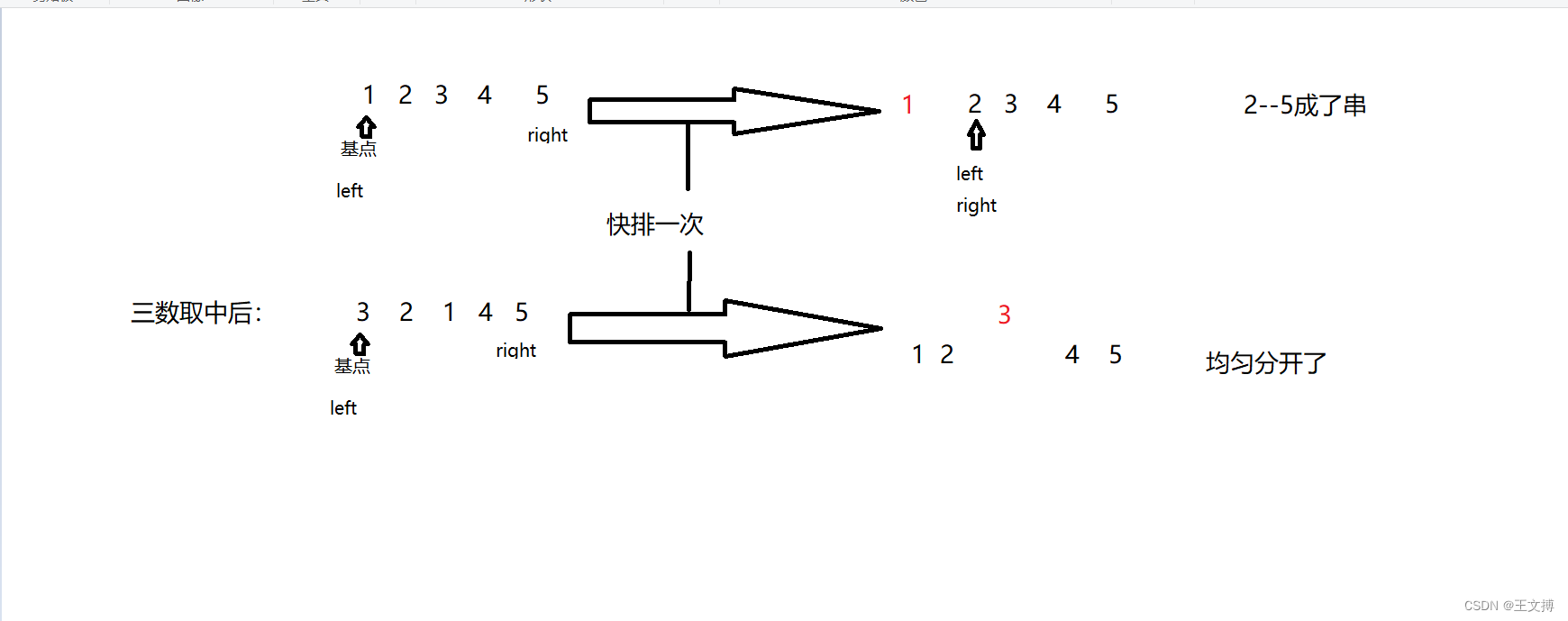
思想：三数取中法，index是每次左右短点和中间点第二大的数字，防止分组不太对称，成为串，这样时间复杂度变高

public static void quick(int [] array){
        int start=0,end=array.length-1;
        quickSort(array,start,end);
    }
    private static void quickSort(int [] array,int start,int end){
        if(start>=end)return;
        //三数取中法，index是每次左右短点和中间点第二大的数字
        //防止分组不太对称，成为串，这样时间复杂度变高
        int index=indexleNum(array,start,end);
        //快排排序开始
        int mid=sort(array,start,end);
        quickSort(array,start,mid-1);
        quickSort(array,mid+1,end);
    }
    //挖坑法
    private static int sort(int [] array,int left,int right){
        int tmp=array[left];//基准
        int i=left;
        //先写右的right--，否则一遍走到left==right后与i下标交换的那一次且仅仅一次将会不有序
        while (left<right) {
            while (left < right && tmp <=array[right]) right--;//找到比tmp小的数
            array[left]=array[right];
            while (left < right && tmp >= array[left]) left++;//找到比tmp大的数
            array[right]=array[left];
        }
        array[left]=tmp;//最后入坑
        return left;//left==right==mid
    }
    private static int indexleNum(int [] array,int left,int right){
        int index=left+((left+right)/2);
        //也就三个数据，空间复杂度不高，所以可以建立一个新的数组，用冒泡
        int [] b=new int[3];
        for (int i = 0; i < b.length-1; i++) {
            boolean flag=false;
            for (int j = 0; j < array.length-1; j++) {
                if (array[j]>array[j+1]){
                    swap(j,j+1,array);
                    flag=true;
                }
            }
            if (flag==false)break;
        }
        return b[1];
    }
    private static void swap(int i ,int j,int [] array){
        int tmp=array[i];
        array[i]=array[j];
        array[j]=tmp;
    }

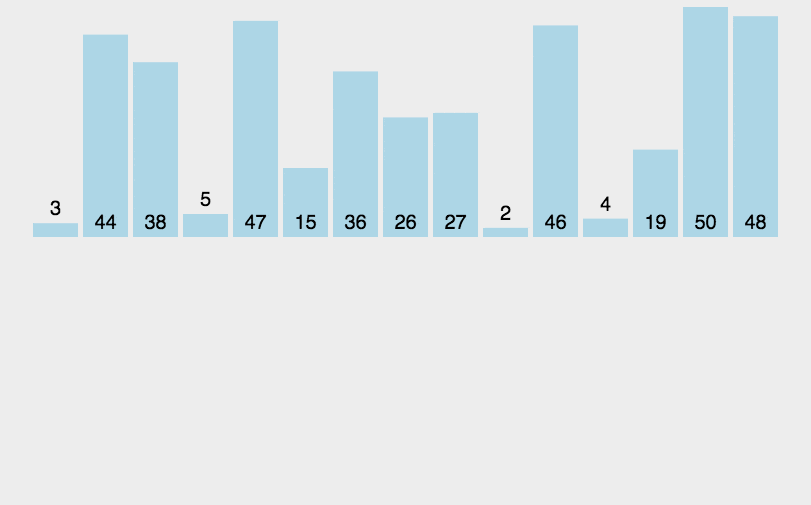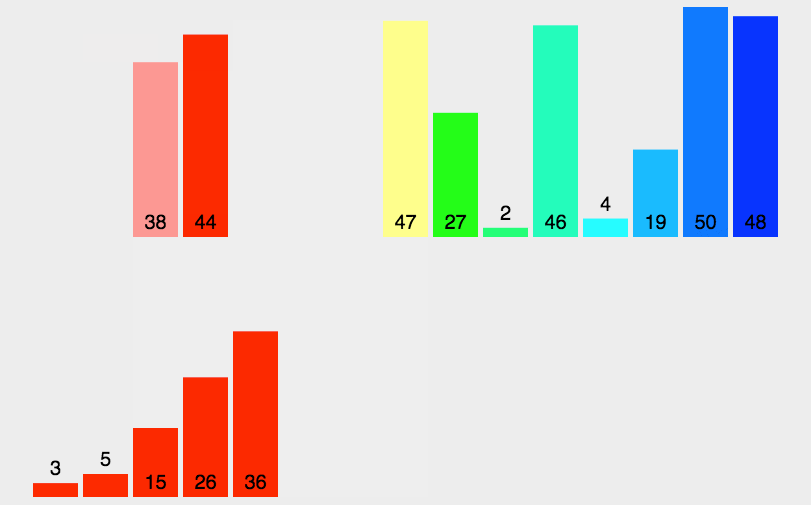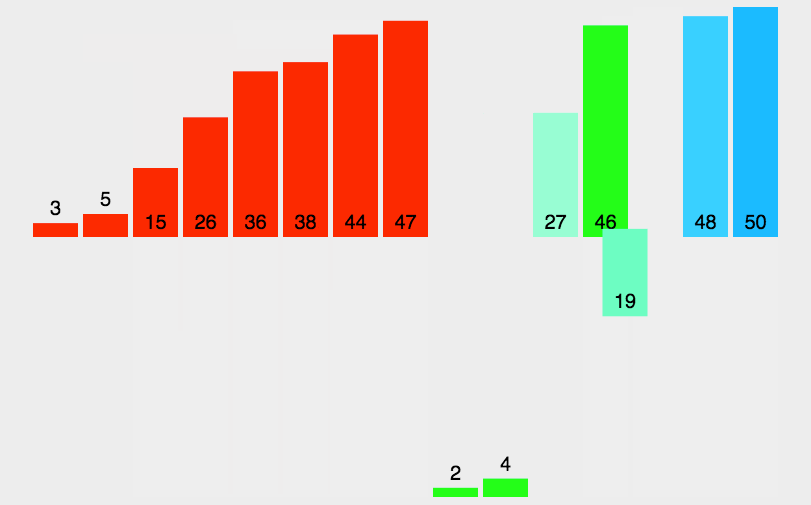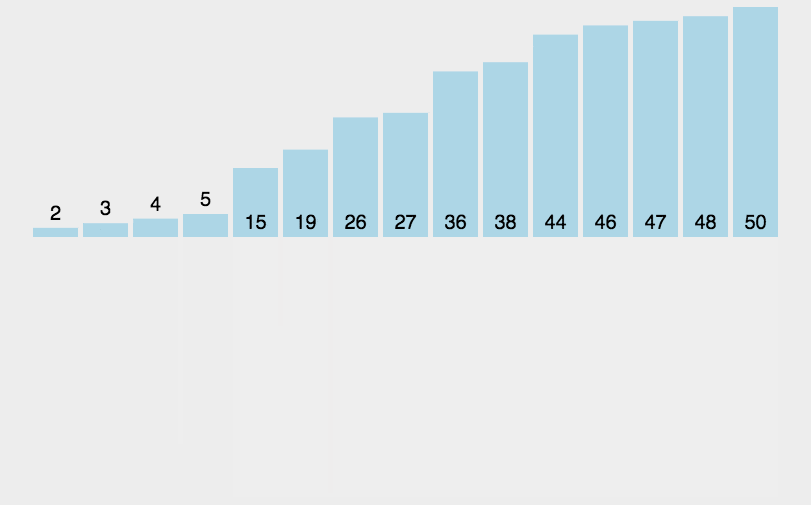
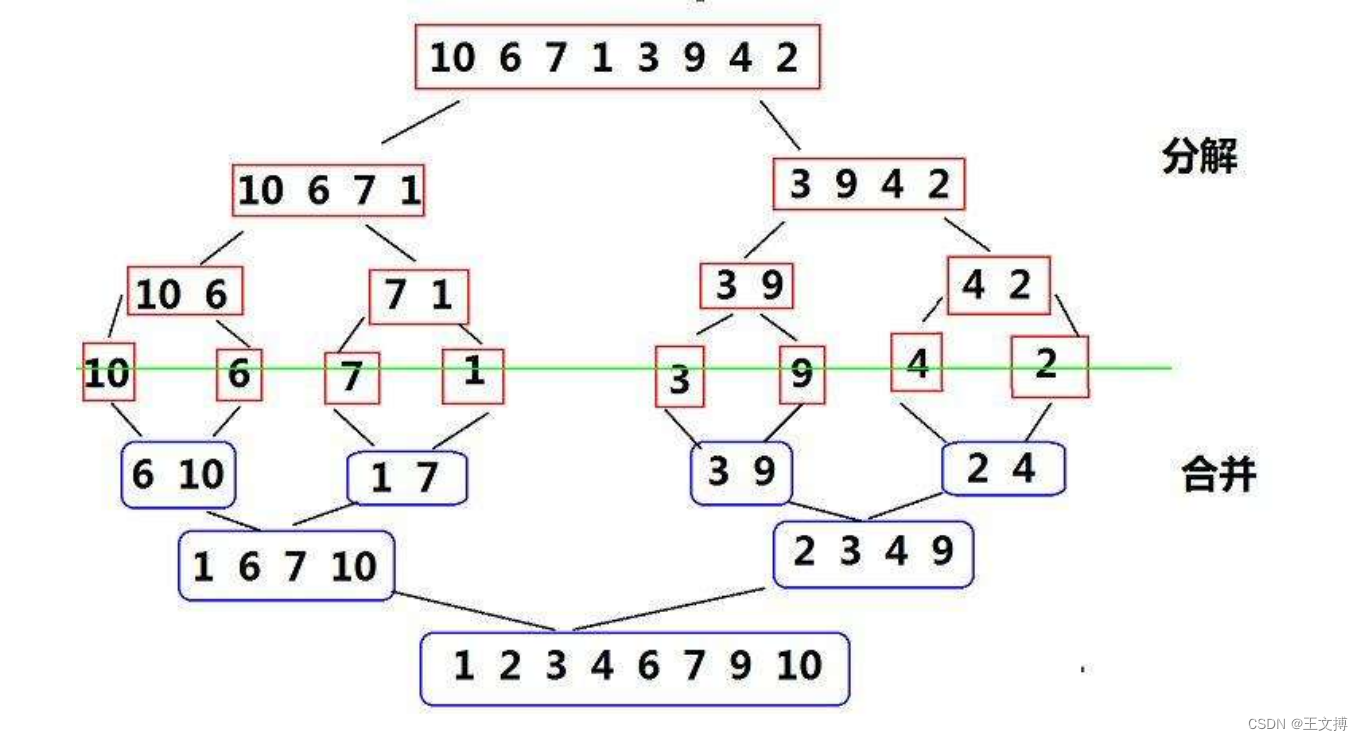
7、归并排序

时间复杂度:O(Nlog2(N)),空间复杂度O(N)

 

 public static void mergerSort(int [] array){
        mergeFunc(array,0,array.length-1);
    }
    private static void mergeFunc(int [] array,int left,int right){
        if(left>=right){
            return;
        }
        int mid=left+((right-left)>>1);
        mergeFunc(array,left,mid);
        mergeFunc(array,mid+1,right);
        //左右拆分完毕，开始合并
        merge(array,mid,left,right);
    }
    private static void merge(int []array,int mid,int left,int right){
        int start1=left;
        int end1=mid;
        int start2=mid+1;
        int end2=right;
        int [] tmp=new int[right-left+1];
        int k=0;
        //保证两个表都有数据
        while (start1<=end1&&start2<=end2){
            if (array[start1]<=array[start2])tmp[k++]=array[start1++];
            else {
                tmp[k++]=array[start2++];
            }
        }
        //如果s2没有数据了但是s1中还有数据
        while (start1<=end1)tmp[k++]=array[start1++];
        //如果s1没有数据了但是s2中还有数据
        while (start2<=end2)tmp[k++]=array[start2++];
        //放回到原来数组
        for (int i = 0; i < k; i++) {
            array[i+left]=tmp[i];//i+left防止覆盖数据
        }
    }

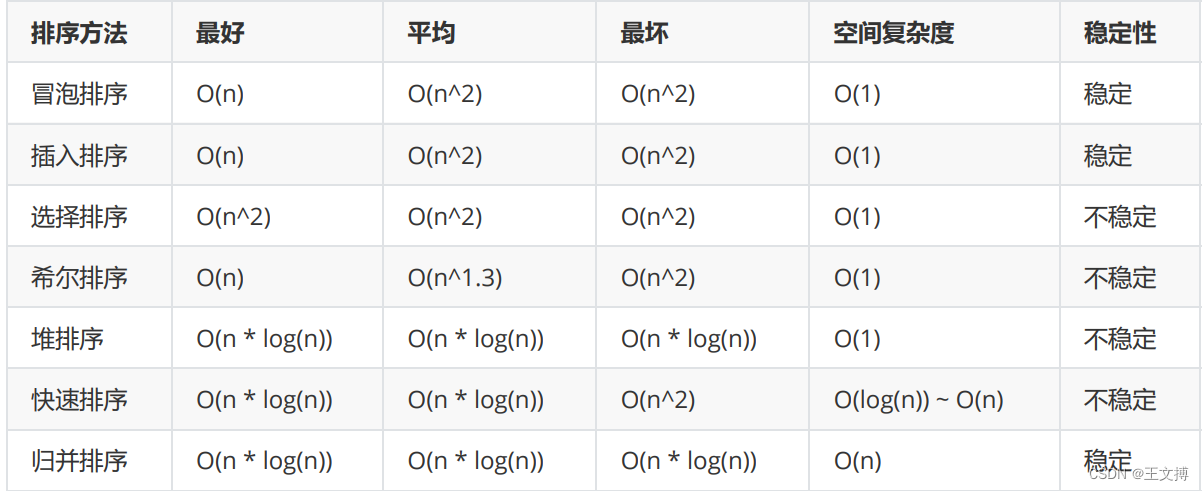
8、总结