力扣日记:【回溯算法篇】39. 组合总和
日期:2023.1.25
参考:代码随想录、力扣
39. 组合总和
题目描述
难度:中等
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
提示:
- 1 <= candidates.length <= 30
- 2 <= candidates[i] <= 40
- candidates 的所有元素 互不相同
- 1 <= target <= 40
题解
class Solution {
public:
#define SOLUTION 2
#if SOLUTION == 1
vector<int> path;
vector<vector<int>> results;
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
backtracking(candidates, target, 0, 0);
return results;
}
// sum 记录当前组合总和,startindex记录当前正在从哪一个元素开始遍历
void backtracking(vector<int>& candidates, int target, int sum, int startindex) {
if (sum > target) return;
if (sum == target) {
results.push_back(path);
return;
}
for (int i = startindex; i < candidates.size(); i++) {
path.push_back(candidates[i]);
backtracking(candidates, target, sum + candidates[i], i); // starindex = i, 而不是 i + 1, 则可重复取自身,但不能取前面的值
path.pop_back();
}
}
#elif SOLUTION == 2 // 剪枝优化
// 实际上本题的输入不一定是有序的
// 假设输入都是有序的(先对输入进行排序),则在for循环遍历时,可以通过以下方法进行剪枝:
// 如果sum + 下一个要加的值(即sum + candidates[i])已经比target大了,则不需要再继续for循环遍历
// 即条件还需要有 sum + candidates[i] <= target
// (如果没有这个剪枝,即使sum已经大于target也会继续遍历递归并在递归中return)
vector<int> path;
vector<vector<int>> results;
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
sort(candidates.begin(), candidates.end()); // 需要排序
backtracking(candidates, target, 0, 0);
return results;
}
// sum 记录当前组合总和,startindex记录当前正在从哪一个元素开始遍历
void backtracking(vector<int>& candidates, int target, int sum, int startindex) {
// if (sum > target) return; // 剪枝后这个不需要了(因为<=target才会进入递归)
if (sum == target) {
results.push_back(path);
return;
}
for (int i = startindex; i < candidates.size() && sum + candidates[i] <= target; i++) {
path.push_back(candidates[i]);
backtracking(candidates, target, sum + candidates[i], i); // starindex = i, 而不是 i + 1, 则可重复取自身,但不能取前面的值
path.pop_back();
}
}
#endif
};
复杂度
时间复杂度:O(n * 2^n)
空间复杂度:O(target)
TODO:怎么算?每个元素都要与集合中所有元素判断(弹入和弹出即为2),n * 2*n ?
思路总结
-
思路:
- 最开始的时候,由于看到题目同一个数字可以无限制重复被选取,就直接取消了 216. 组合总和 III 问题中 使用的
startindex,这样每次for循环都从头遍历一遍集合,肯定可以重复取,但运行后看到:
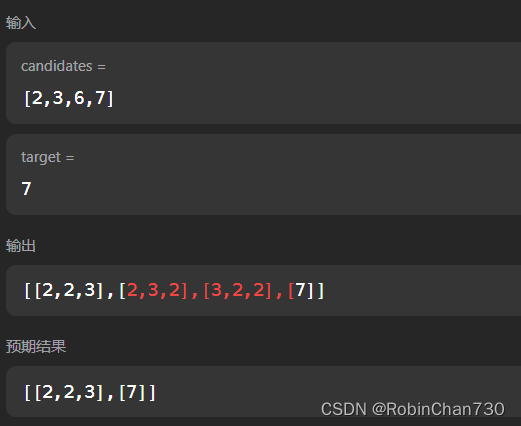
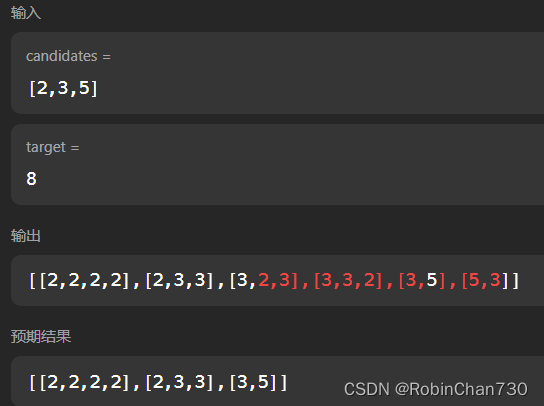
发觉这样存在一个问题,就是for循环从头遍历会取到当前元素之前的元素,导致结果集存在重复的组合(如[3,2,3]与[2,3,3]重复,就是因为把3放入path后,下一层递归还从2开始取值),因此要避免选到之前的元素,但又要能重复选取到自身,所以在递归时设置startindex = i,表示从当前遍历到的元素重新开始遍历,即可解决问题。 - 对于终止条件,则是通过 sum 进行判断
- 除此之外,其他思路与 216. 组合总和 III 问题类似,套用模板即可。
- 对比两道题目,都是从同一个元素取值,因此都需要
startindex,但是 第216题 中不能重复取自身,所以每次for循环在递归的时候startindex = i + 1;但本题可以重复取自身,所以startindex = i。且前者一定是k个数的组合,所以终止条件可以通过path.size() == k来判断;但本题不然,只能通过sum > target或sum == target判断 - 树状结构示意图:
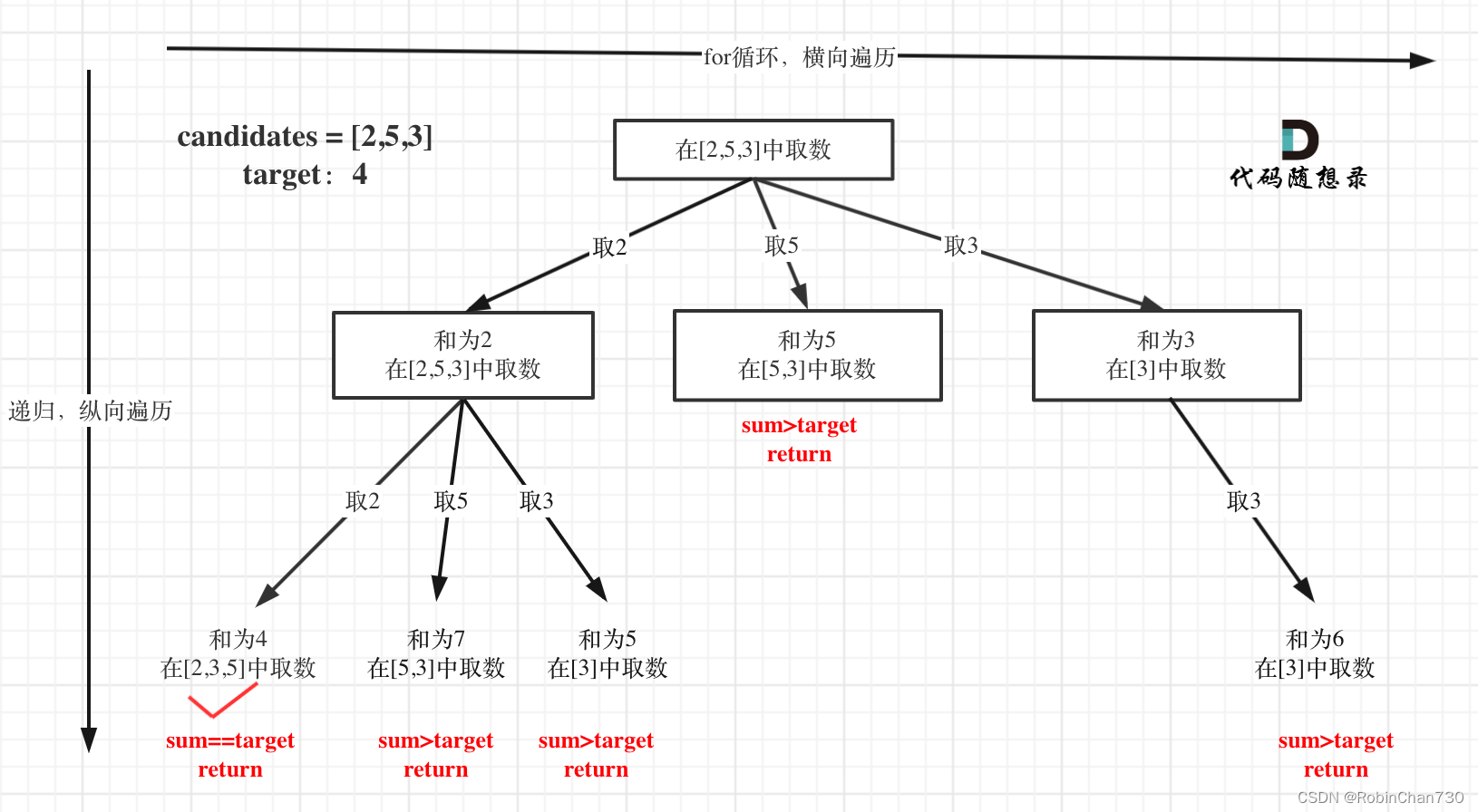
- 最开始的时候,由于看到题目同一个数字可以无限制重复被选取,就直接取消了 216. 组合总和 III 问题中 使用的
-
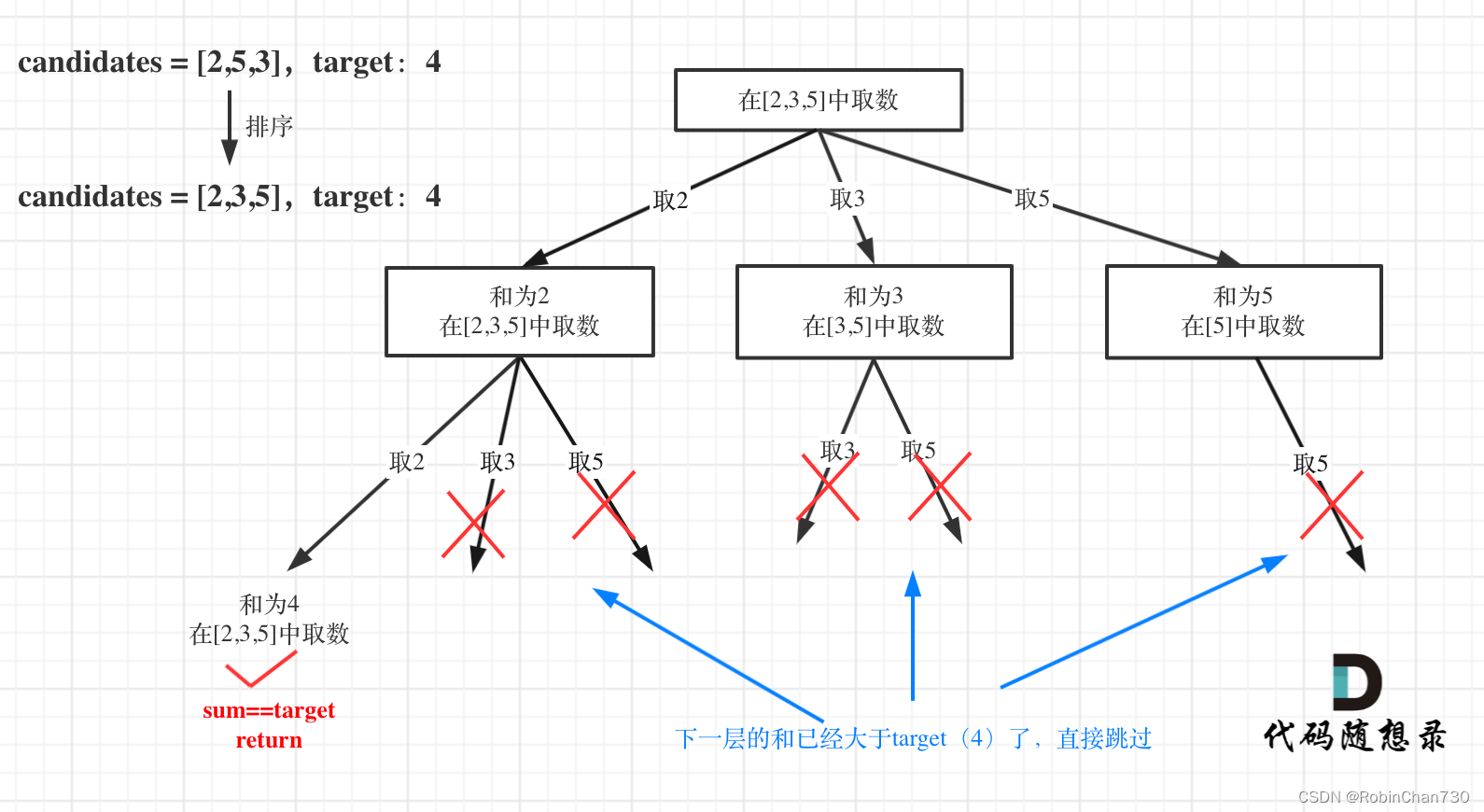
剪枝优化:
- 实际上本题的输入不一定是有序的,假设输入都是有序的(先对输入进行排序),则在for循环遍历时,可以通过以下方法进行剪枝:
- 如果sum + 下一个要加的值(即sum + candidates[i])已经比target大了,则不需要再继续for循环遍历
- 即条件还需要有 sum + candidates[i] <= target
- (如果没有这个剪枝,即使sum已经大于target也会继续遍历后面的值进行递归并在递归中return)
- 示意图:
-
套路总结(by 代码随想录):
- 对于组合问题,什么时候需要startIndex呢:
- 如果是一个集合来求组合的话,就需要startIndex,例如:77.组合,216.组合总和III。
- 如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:17.电话号码的字母组合
- 在求和问题中,排序之后加剪枝是常见的套路!
- 对于组合问题,什么时候需要startIndex呢:







![[足式机器人]Part2 Dr. CAN学习笔记- 最优控制Optimal Control Ch07-4 轨迹追踪](https://img-blog.csdnimg.cn/direct/40f20d6d28c74c3a981944c5315bfd56.png#pic_center)