目录
源算子
转换算子
1,基本转换算子
1.1映射(map)
1.2过滤(filter)
1.3扁平映射(flatMap)
2,聚合算子
2.1按键分区(keyBy)
2.2简单聚合
3,用户自定义函数
3.1.函数类(Function Classes)
3.2 富函数类(Rich Function Classes)
4,物理分区
输出算子
源算子
源算子
转换算子
1,基本转换算子
1.1映射(map)
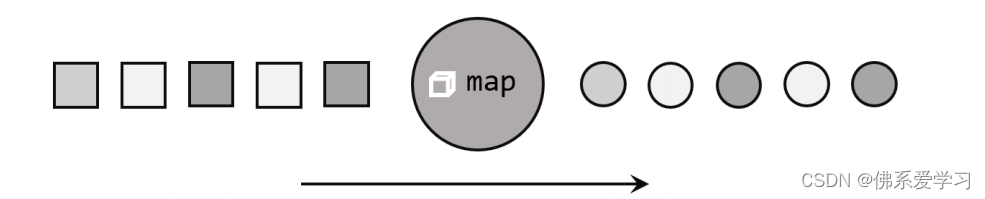
Map() 是大数据处理中常用的一个算子,主要用于转换数据流中的数据,生成新的数据流。这个操作可以看作是一种“一一映射”,即对输入数据流中的每个元素进行处理,并产生一个相应的输出元素。在处理大量数据时,Map() 算子能够帮助我们将复杂的数据转换成易于处理或符合特定需求的格式。通过定义一个函数或Lambda表达式,我们可以指定如何对输入数据进行转换。Map() 算子在处理数据流时非常灵活,可以应用于各种场景,如数据清洗、格式转换、特征提取等。
1.2过滤(filter)

Filter() 转换操作是对数据流执行过滤的过程,根据指定的布尔条件表达式来设置过滤条件。对于流中的每个元素,Filter() 算子会根据条件进行判断:如果条件为真(true),则元素正常输出;如果条件为假(false),则元素被过滤掉。这种过滤操作在大数据处理中非常有用,可以用于筛选出符合特定条件的数据,或者去除不符合要求的数据。通过 Filter() 算子,我们可以实现对数据流的筛选、去重、降噪等操作,从而更好地处理和分析数据。与 Map() 算子一样,Filter() 算子也提供了很大的灵活性,可以根据具体需求自定义过滤条件。在 Flink 中,我们可以通过实现一个函数或 Lambda 表达式来定义过滤条件,从而实现数据的筛选操作。
1.3扁平映射(flatMap)

FlatMap() 操作又称为扁平映射,主要用于将数据流中的整体(通常是集合类型)拆分成单个个体。与 Map() 算子不同,FlatMap() 可以产生 0 到多个元素,意味着对于输入数据流中的每个元素,FlatMap() 可以根据定义的处理逻辑生成一个或多个输出元素。这种操作在大数据处理中非常有用,特别是在需要对集合类型数据进行拆分和转换的场景中。
FlatMap() 可以被视为“扁平化”(flatten)和“映射”(map)两个操作的结合。具体来说,它首先按照某种规则将数据进行打散拆分,然后将拆分后的元素进行转换处理。这种操作在数据流处理中提供了一种有效的机制,用于处理复杂的转换逻辑,特别是需要将集合类型数据拆分成单个元素进行处理的情况。
2,聚合算子
2.1按键分区(keyBy)
在 Flink 中,DataStream API 本身不直接提供聚合操作。对海量数据进行聚合时,为了提高效率,我们需要进行分区并行处理。因此,在 Flink 中进行聚合之前,通常需要先进行分区操作。这个分区操作是通过 keyBy() 算子完成的。
keyBy() 算子在聚合操作中起着至关重要的作用。通过指定键(key),它可以将一条数据流逻辑上划分成不同的分区(partitions)。这些分区实际上是并行处理的子任务,每个分区对应一个任务槽(task slot)。
当使用不同的键时,流中的数据将被分配到不同的分区中。这样一来,所有具有相同键的数据都会被发送到同一个分区,从而确保后续的算子操作在同一个任务槽中执行。这种分区机制确保了相同键的数据能够被集中处理,提高了聚合操作的效率。
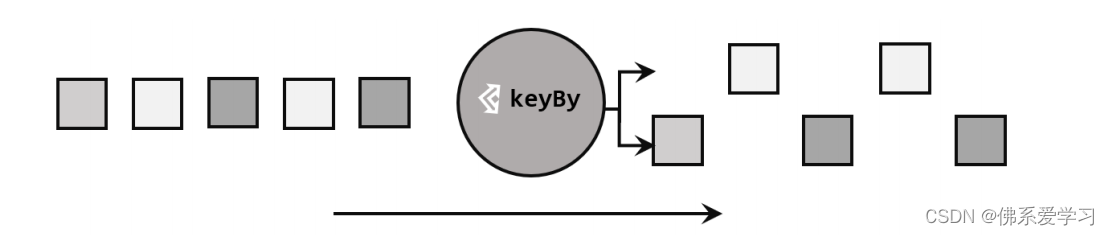
在内部,keyBy() 算子通过计算键的哈希值并对分区数进行取模运算来实现数据的分区。因此,如果键是一个 POJO 类,必须重写其 hashCode() 方法以确保正确的哈希计算。
在具体使用时,keyBy() 方法需要传入一个参数,这个参数可以是一个或一组键。有多种方式指定键:对于 Tuple 数据类型,可以指定字段的位置或多个位置的组合;对于 POJO 类型或 Scala 的样例类,可以指定字段的名称(String);此外,还可以使用 Lambda 表达式或实现一个键选择器(KeySelector)来描述从数据中提取键的逻辑。
通过合理使用 keyBy() 算子,开发者能够有效地对数据进行分区处理,从而实现高效的聚合操作。这为处理大规模数据流提供了强有力的支持,并确保了 Flink 流处理的灵活性和可扩展性。
2.2简单聚合
在拥有按键分区的 KeyedStream 数据流后,我们就可以基于它进行聚合操作了。Flink 为我们提供了一些内置的基本和简单聚合 API,主要包括以下几种:
- sum():在输入流上,对指定的字段执行叠加求和操作。
- min():在输入流上,对指定的字段求最小值。
- max():在输入流上,对指定的字段求最大值。
- minBy():与 min() 类似,但在输入流上针对指定字段求最小值。不同的是,min() 只计算指定字段的最小值,而其他字段会保留最初第一个数据的值;而 minBy() 会返回包含字段最小值的整条数据。
- maxBy():与 max() 类似,在输入流上针对指定字段求最大值。与 min()/minBy() 的区别相同。
这些聚合算子使用起来非常方便,语义也非常明确。调用这些聚合方法时,需要传入参数,但不像基本转换算子那样需要实现自定义函数。只要指定聚合指定的字段即可。字段的指定有两种方式:通过位置或通过名称。
对于元组类型的数据,同样可以使用这两种方式来指定字段。需要注意的是,元组中的字段名称是以 _1、_2、_3 等来命名的。
通过这些聚合算子,我们可以轻松地对按键分区的数据进行聚合操作,从而快速获得所需的数据摘要或统计信息。
3,用户自定义函数
在 Apache Flink 的 DataStream API 中,编程风格确实是一致的。基于 DataStream 的转换操作主要通过一系列的方法调用实现,每个方法都对应一个特定的算子操作。这些方法通常需要传入一个参数,这个参数是一个实现了特定接口的对象。
这些接口都遵循一个统一的命名规范,即以算子操作名称 + Function 结尾,如 SourceFunction、MapFunction、ReduceFunction 等。这种命名约定有助于开发者快速识别接口的用途。
用户可以通过多种方式实现这些接口:
3.1.函数类(Function Classes)
在处理流数据时,大部分操作都需要使用到用户自定义函数(UDF)。这些函数通过实现特定的接口,如 MapFunction、FilterFunction、ReduceFunction 等,来定义数据的处理逻辑。
3.2 富函数类(Rich Function Classes)
富函数类是 DataStream API 提供的一种特殊的函数类接口,它们都有一个 Rich 版本。与常规函数类相比,富函数类提供了更多的功能和更大的灵活性。
首先,所有的 Flink 函数类都有其 Rich 版本,如 RichMapFunction、RichFilterFunction、RichReduceFunction 等。这些富函数类通常以抽象类的形式出现,为开发者提供了一个基类,用于实现更复杂的功能。
与常规函数类的主要区别在于,富函数类可以获取运行环境的上下文,并拥有一些生命周期方法。这使得它们能够实现更高级的功能,比如获取执行环境的信息、访问外部资源或执行更复杂的初始化操作。
以下是生命周期方法的一些关键点:
- open()方法:这是 Rich Function 的初始化方法,标志着算子生命周期的开始。在算子的实际工作方法(如 map() 或 filter())被调用之前,open() 方法会被首先调用。因此,一次性工作,如文件 IO 流的创建、数据库连接的建立或配置文件的读取等,都适合在 open() 方法中完成。
- close()方法:这是生命周期中的最后一个方法,类似于对象的解构方法。它通常用于执行清理工作,例如释放资源或关闭打开的连接。
需要注意的是,对于一个并行子任务来说,生命周期方法只会调用一次;而实际的工作方法(如 RichMapFunction 中的 map()),则在每条数据到达时都会被触发一次调用。
通过使用富函数类,开发者可以更好地控制数据处理过程中的行为和资源管理,从而实现更高效和灵活的数据处理任务。
4,物理分区
分区操作在数据处理中是一个核心概念,它涉及到将数据重新分配到不同的子集或分区,以便进行更高效或更有针对性的处理。分区操作通常用于流处理和批处理系统,以提高数据处理的速度和效率。
在 Apache Flink 这样的流处理框架中,"keyBy()" 方法是一个逻辑分区操作。逻辑分区主要是基于某个或某些键值(key)对数据进行分组,以便于进行聚合、窗口操作等后续计算。
然而,仅仅通过逻辑分区可能并不足以满足所有的数据处理需求。因此,Flink 提供了一系列物理分区操作算子,用于在数据流经过转换操作之后,进行更细致和特定的分区。这些物理分区操作主要包括:
1,随机分区:将数据随机分配到不同的分区,以达到负载均衡的目的。
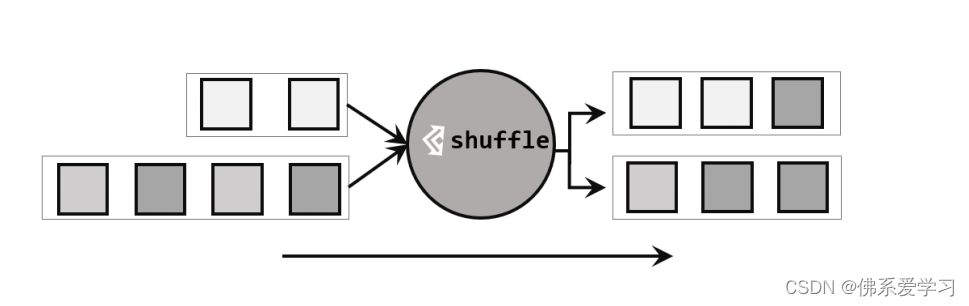
2,轮询分区:按照固定的顺序将数据分配到不同的分区,通常用于保证数据的顺序性。
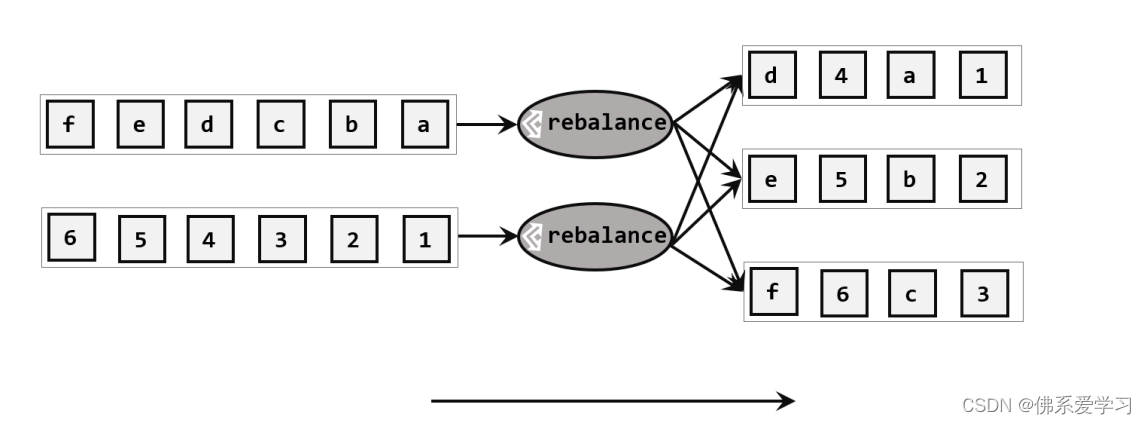
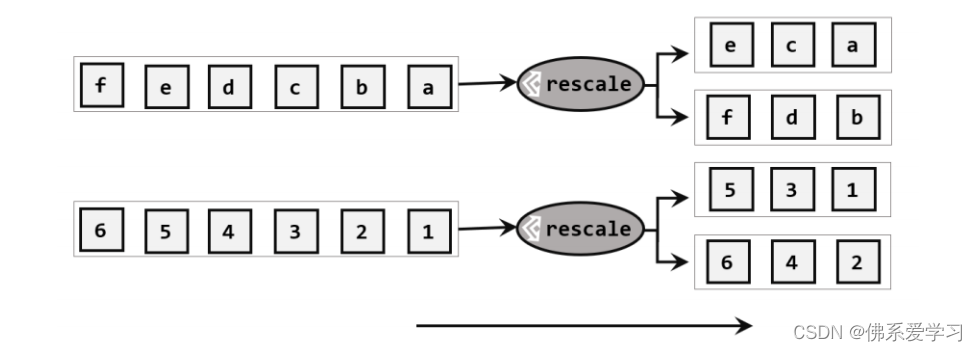
3,重缩放分区:根据数据的分布情况动态调整分区的数量,以实现更好的负载均衡。
4,广播:将数据同时发送到所有分区,主要用于全局状态的管理或同步。
5,全局分区:将所有数据分配到一个分区中,通常用于全局聚合或统计。
此外,Flink 还支持用户自定义分区策略,以满足特定的业务需求。用户可以根据自己的数据特性和处理逻辑,编写自定义的分区函数,以实现更精细的数据处理逻辑。
分区操作在流处理中起着至关重要的作用,通过合理的分区策略和操作,可以提高数据处理的效率、准确性和响应速度。
输出算子
输出算子

![[足式机器人]Part2 Dr. CAN学习笔记- 最优控制Optimal Control Ch07-4 轨迹追踪](https://img-blog.csdnimg.cn/direct/40f20d6d28c74c3a981944c5315bfd56.png#pic_center)