[NOI2018] 冒泡排序
题目背景
请注意,题目中存在 n = 0 n=0 n=0 的数据。
题目描述
最近,小 S 对冒泡排序产生了浓厚的兴趣。为了问题简单,小 S 只研究对 1 1 1 到 n n n 的排列的冒泡排序。
下面是对冒泡排序的算法描述。
输入:一个长度为 n 的排列 p[1...n]
输出:p 排序后的结果。
for i = 1 to n do
for j = 1 to n - 1 do
if(p[j] > p[j + 1])
交换 p[j] 与 p[j + 1] 的值
冒泡排序的交换次数被定义为交换过程的执行次数。可以证明交换次数的一个下界是 1 2 ∑ i = 1 n ∣ i − p i ∣ \frac 1 2 \sum_{i=1}^n \lvert i - p_i \rvert 21∑i=1n∣i−pi∣,其中 p i p_i pi 是排列 p p p 中第 i i i 个位置的数字。如果你对证明感兴趣,可以看提示。
小 S 开始专注于研究长度为 n n n 的排列中,满足交换次数 = 1 2 ∑ i = 1 n ∣ i − p i ∣ = \frac 1 2 \sum_{i=1}^n \lvert i - p_i \rvert =21∑i=1n∣i−pi∣ 的排列(在后文中,为了方便,我们把所有这样的排列叫「好」的排列)。他进一步想,这样的排列到底多不多?它们分布的密不密集?
小 S 想要对于一个给定的长度为 n n n 的排列 q q q,计算字典序严格大于 q q q 的“好”的排列个数。但是他不会做,于是求助于你,希望你帮他解决这个问题,考虑到答案可能会很大,因此只需输出答案对 998244353 998244353 998244353 取模的结果。
输入格式
输入第一行包含一个正整数 T T T,表示数据组数。
对于每组数据,第一行有一个正整数 n n n,保证 n ≤ 6 × 1 0 5 n \leq 6 \times 10^5 n≤6×105。
接下来一行会输入 n n n 个正整数,对应于题目描述中的 q i q_i qi,保证输入的是一个 1 1 1 到 n n n 的排列。
输出格式
输出共 T T T 行,每行一个整数。
对于每组数据,输出一个整数,表示字典序严格大于 q q q 的「好」的排列个数对 998244353 998244353 998244353 取模的结果。
样例 #1
样例输入 #1
1
3
1 3 2
样例输出 #1
3
样例 #2
样例输入 #2
1
4
1 4 2 3
样例输出 #2
9
提示
更多样例
更多样例请在附加文件中下载。
样例 3
见附加文件中的 inverse3.in 与 inverse3.ans。
样例 1 解释
字典序比 1 3 2 1 \ 3 \ 2 1 3 2 大的排列中,除了 3 2 1 3 \ 2 \ 1 3 2 1 以外都是「好」的排列,故答案为 3 3 3。
数据范围
下面是对本题每个测试点的输入规模的说明。
对于所有数据,均满足 T = 5 T = 5 T=5(样例可能不满足)。
记 n m a x n_\mathrm{max} nmax 表示每组数据中 n n n 的最大值, ∑ n \sum n ∑n 表示所有数据的 n n n 的和。
| 测试点 | n m a x = n_\mathrm{max} = nmax= | ∑ n ≤ \sum n \leq ∑n≤ | 特殊性质 |
|---|---|---|---|
| 1 | 8 8 8 | 5 n m a x 5 \ n_\mathrm{max} 5 nmax | 无 |
| 2 | 9 9 9 | 5 n m a x 5 \ n_\mathrm{max} 5 nmax | 无 |
| 3 | 10 10 10 | 5 n m a x 5 \ n_\mathrm{max} 5 nmax | 无 |
| 4 | 12 12 12 | 5 n m a x 5 \ n_\mathrm{max} 5 nmax | 无 |
| 5 | 13 13 13 | 5 n m a x 5 \ n_\mathrm{max} 5 nmax | 无 |
| 6 | 14 14 14 | 5 n m a x 5 \ n_\mathrm{max} 5 nmax | 无 |
| 7 | 16 16 16 | 5 n m a x 5 \ n_\mathrm{max} 5 nmax | 无 |
| 8 | 16 16 16 | 5 n m a x 5 \ n_\mathrm{max} 5 nmax | 无 |
| 9 | 17 17 17 | 5 n m a x 5 \ n_\mathrm{max} 5 nmax | 无 |
| 10 | 18 18 18 | 5 n m a x 5 \ n_\mathrm{max} 5 nmax | 无 |
| 11 | 18 18 18 | 5 n m a x 5 \ n_\mathrm{max} 5 nmax | 无 |
| 12 | 122 122 122 | 700 700 700 | ∀ i q i = i \forall i \enspace q_i = i ∀iqi=i |
| 13 | 144 144 144 | 700 700 700 | 无 |
| 14 | 166 166 166 | 700 700 700 | 无 |
| 15 | 200 200 200 | 700 700 700 | 无 |
| 16 | 233 233 233 | 700 700 700 | 无 |
| 17 | 777 777 777 | 4000 4000 4000 | ∀ i q i = i \forall i \enspace q_i = i ∀iqi=i |
| 18 | 888 888 888 | 4000 4000 4000 | 无 |
| 19 | 933 933 933 | 4000 4000 4000 | 无 |
| 20 | 1000 1000 1000 | 4000 4000 4000 | 无 |
| 21 | 266666 266666 266666 | 2000000 2000000 2000000 | ∀ i q i = i \forall i \enspace q_i = i ∀iqi=i |
| 22 | 333333 333333 333333 | 2000000 2000000 2000000 | 无 |
| 23 | 444444 444444 444444 | 2000000 2000000 2000000 | 无 |
| 24 | 555555 555555 555555 | 2000000 2000000 2000000 | 无 |
| 25 | 600000 600000 600000 | 2000000 2000000 2000000 | 无 |
提示
下面是对交换次数下界是 1 2 ∑ i = 1 n ∣ i − p i ∣ \frac 1 2 \sum_{i=1}^n \lvert i - p_i \rvert 21∑i=1n∣i−pi∣ 的证明。
排序本质上就是数字的移动,因此排序的交换次数应当可以用数字移动的总距离来描述。对于第 i i i 个位置,假设在初始排列中,这个位置上的数字是 pi,那么我们需要将这个数字移动到第 p i p_i pi 个位置上,移动的距离是 ∣ i − p i ∣ \lvert i - p_i \rvert ∣i−pi∣。从而移动的总距离就是 ∑ i = 1 n ∣ i − p i ∣ \sum_{i=1}^n \lvert i - p_i \rvert ∑i=1n∣i−pi∣,而冒泡排序每次会交换两个相邻的数字,每次交换可以使移动的总距离至多减少 2 2 2。因此 1 2 ∑ i = 1 n ∣ i − p i ∣ \frac 1 2 \sum_{i=1}^n \lvert i - p_i \rvert 21∑i=1n∣i−pi∣ 是冒泡排序的交换次数的下界。
并不是所有的排列都达到了下界,比如在 n = 3 n = 3 n=3 的时候,考虑排列 3 2 1 3 \ 2 \ 1 3 2 1,这个排列进行冒泡排序以后的交换次数是 3 3 3,但是 1 2 ∑ i = 1 n ∣ i − p i ∣ \frac 1 2 \sum_{i=1}^n \lvert i - p_i \rvert 21∑i=1n∣i−pi∣ 只有 2 2 2。
感谢给我讲了这个题的神仙跳瓜 jumpmelon\textrm{jumpmelon}jumpmelon。
首先看给的提示,我们可以发现在这样的排序方式下,对于每一个数都只向目标位置方向走,不换向。那么对于一个数 xxx,如果有一个比它大的数在它前面,那么它必须向左走;如果有一个比它小的数在它后面,那么它必须向右走。这样的排列是不合法的,即要求不存在长度超过 222 的下降子序列。
根据 Dilworth\textrm{Dilworth}Dilworth 定理,最长下降子序列的长度不超过 222,即整个排列最多被划分成 222 个上升子序列。
先不考虑字典序严格大于 qqq 的限制。
我们记 fi,jf_{i, j}fi,j 为前 iii 个的最大值为 jjj 后面 n−in - in−i 个位置的方案数。我们考虑第 iii 个数填什么。注意 i⩽ji \leqslant ji⩽j
如果填比 jjj 大的数,那么一定可以接在 jjj 的后面;如果要填比 jjj 小的数,那么必须填当前还没有填的中最小的,否则上升子序列将不止 222 个,所以
fi,j={fi+1,k (k>j)fi+1,j =∑k=jnfi+1,k\begin{aligned} f_{i, j} &= \begin{cases} f_{i + 1, k} \ \ \ \ \ (k > j) \\ f_{i + 1, j} \ \ \ \ \ \end{cases} \\ &= \sum_{k = j}^n f_{i + 1, k} \end{aligned} fi,j={fi+1,k (k>j)fi+1,j =k=j∑nfi+1,k
但是直接这样递推是 O(n2)O(n^2)O(n2) 的。我们把它以图像的形式表示,fi,jf_{i, j}fi,j 即表示从点 (i,j)(i, j)(i,j) 开始,每次向右走一步,向上走 x(x⩽0)x(x \leqslant 0)x(x⩽0) 步,不与直线 y=x−1y = x - 1y=x−1 (因为 i⩽ji \leqslant ji⩽j) 相交,走到点 (n,n)(n, n)(n,n) 的方案数。
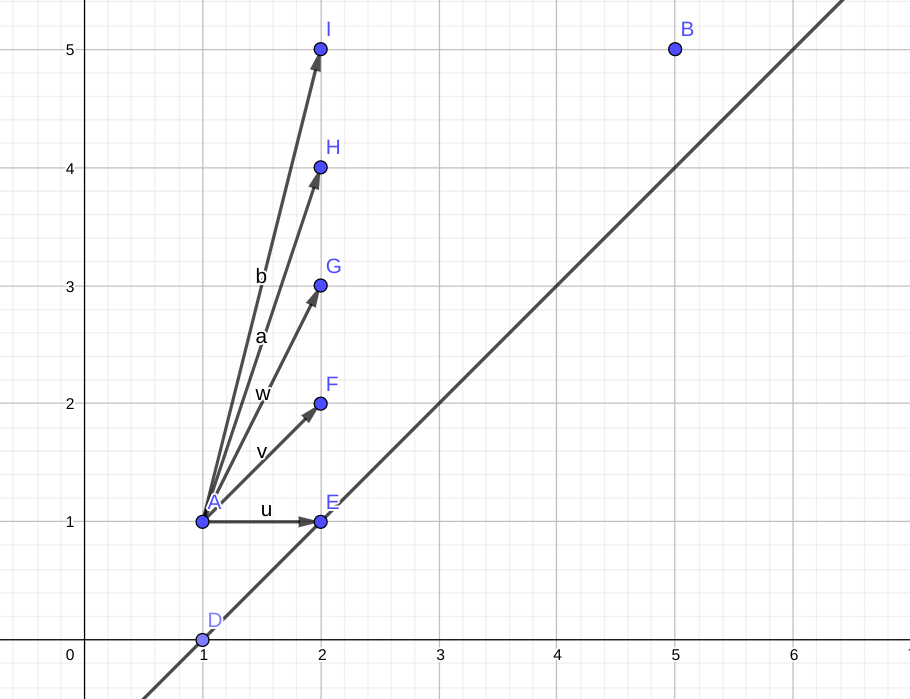
如图,即从点 A(i,j)A(i, j)A(i,j) 走到 B(n,n)B(n, n)B(n,n) 的不与直线 y=x−1y = x - 1y=x−1 相交的方案数。
首先,如果不考虑与直线不相交,即为走 n−in - in−i 次,每次选择向上走 x(x⩾0)x (x \geqslant 0)x(x⩾0) 步,一共走了 n−jn - jn−j 步的方案数。模仿插板法,因为 xxx 可以取 000,我们把总个数加上划分数 n−in - in−i,变成 n−i+n−jn - i + n - jn−i+n−j 个物品划分成 n−in - in−i 块的方案数,即 (2n−i−j−1n−i−1)\dbinom{2n - i - j - 1}{n-i-1}(n−i−12n−i−j−1)。
再模仿 Catalan\textrm{Catalan}Catalan 数的推法,看第一个与直线 y=x−1y = x - 1y=x−1 相交的位置。找点 (i,j)(i, j)(i,j) 关于直线 y=x−1y = x - 1y=x−1 的对称点 (j+1,i−1)(j + 1, i - 1)(j+1,i−1), 由于方案一一对应,所以,从点 (i,j)(i, j)(i,j) 出发,经过直线的方案数即为从点 (j+1,i−1)(j + 1, i - 1)(j+1,i−1) 出发到点 (n,n)(n, n)(n,n) 的方案数。
得到
fi,j=calc(i,j)−calc(j+1,i−1)=(2n−i−j−1n−i−1)−(2n−i−j−1n−j−2)\begin{aligned} f_{i, j} &= calc(i, j) - calc(j + 1, i - 1) \\ &= \dbinom{2n - i - j - 1}{n - i - 1} - \dbinom{2n - i - j - 1}{n - j - 2} \\ \end{aligned} fi,j=calc(i,j)−calc(j+1,i−1)=(n−i−12n−i−j−1)−(n−j−22n−i−j−1)
这样就得到 fff 的 O(1)O(1)O(1) 求解啦!(然而 O(n2)O(n^2)O(n2) 有足足 808080 分,真香)
可以发现 f0,0f_{0, 0}f0,0 即为 Catalan\textrm{Catalan}Catalan 数,可以得到 121212 分。
回到有限制字典序严格大于 qqq 的原题上来。考虑一位一位枚举,假设当前枚举到第 iii 项,我们计数证前 i−1i - 1i−1 项与 qqq 相同,第 iii 项大于 qiq_iqi 的排列个数。
记 mx=maxj=1i−1qjmx = \max_{j = 1}^{i - 1} q_jmx=maxj=1i−1qj,mnmnmn 为当前还没有用过的最小的数,v=qiv = q_iv=qi。第 iii 位只能填 mnmnmn 或大于 mxmxmx 的数。分类讨论
-
v=mnv = mnv=mn
(因为 mnmnmn 是最小可以填的,所以 vvv 的下界是 mnmnmn。)
此时,第 iii 项不能填 mnmnmn,只能大于 mxmxmx,故后面 n−in - in−i 项的填法有 ∑k=mx+1nfi,k\sum_{k = mx + 1}^n f_{i, k}∑k=mx+1nfi,k 种(kkk 为第 iii 位填的数)。
-
mn<v<mxmn < v < mxmn<v<mx
此时第 iii 位没有可以填的,后面不再存在合法方案。(但是还是要读完)
-
v⩾mxv \geqslant mxv⩾mx
此时第 iii 位可以填 mnmnmn 或大于 mxmxmx 的数,方案数为 ∑k=mxnfi,k\sum_{k = mx}^n f_{i, k}∑k=mxnfi,k。
问题又来了,怎么求 fff 的前缀和呢?考虑 fff 的递推式 fi,j=∑k=jnfi+1,kf_{i, j} = \sum_{k = j}^n f_{i + 1, k}fi,j=∑k=jnfi+1,k,这正是一个前缀和的形式。所以
∑k=limnfi,k=fi−1,lim\sum_{k = lim}^n f_{i, k} = f_{i - 1, lim} k=lim∑nfi,k=fi−1,lim
不用像其他题解上说的要用树状数组,复杂度 O(Tn)O(Tn)O(Tn)(还好写)
完结撒花~
代码
注意数组要开 2n2n2n,写起来很简单,但是最开始由于没彻底搞懂想了半天
#include <bits/stdc++.h>
using namespace std;
namespace TYC
{
typedef long long ll;
const int N = 1.2e6, p = 998244353;
int fac[N + 5], inv[N + 5], vis[N + 5];
inline int read()
{
int v = 0, fl = 0, ch = getchar();
while (!isdigit(ch))
fl |= (ch == '-'), ch = getchar();
while (isdigit(ch))
v = v * 10 + ch - '0', ch = getchar();
return fl ? -v : v;
}
inline int qpow(int v, int tim)
{
int ans = 1;
for (; tim; tim >>= 1, v = (ll)v * v % p)
if (tim & 1)
ans = (ll)ans * v % p;
return ans;
}
void init()
{
fac[0] = 1;
for (int i = 1; i <= N; i++)
fac[i] = (ll)fac[i - 1] * i % p;
inv[N] = qpow(fac[N], p - 2);
for (int i = N; i; i--)
inv[i - 1] = (ll)inv[i] * i % p;
}
inline int C(const int n, const int m)
{
return (n < 0 || m < 0 || n < m) ? 0 : int((ll)fac[n] * inv[m] % p * inv[n - m] % p);
}
int n;
inline int F(const int i, const int j)
{
return i <= j && j <= n ? (C(2 * n - i - j - 1, n - i - 1) - C(2 * n - i - j - 1, n - j - 2) + p) % p : 0;
}
void work()
{
init();
int T = read();
while (T--)
{
n = read();
memset(vis, 0, sizeof(int[n + 1]));
int ans = 0, mx = 0, mn = 1, flag = 0, v;
for (int i = 1; i <= n; i++)
{
v = read();
if (flag)
continue;
ans = (ans + (F(i - 1, max(mx, v) + 1) + p) % p) % p;
if (mx > v && v > mn)
flag = 1;
mx = max(mx, v);
vis[v] = 1;
while (vis[mn]) mn++;
}
printf("%d\n", ans);
}
}
}
int main()
{
TYC::work();
return 0;
}








![[BJDCTF2020]ZJCTF,不过如此(特详解)](https://img-blog.csdnimg.cn/img_convert/3b5dd69949e55aba44679863daea5f13.png)


![[蓝桥杯]真题讲解:冶炼金属(暴力+二分)](https://img-blog.csdnimg.cn/direct/61404e1a397f444f9a21ba10fcccf594.png)