文章目录
- 前言
- Crypto
- not_wiener
前言
比赛没打,赛后随便做一下题目

Crypto
not_wiener
task.py:
from Crypto.Util.number import *
from gmpy2 import *
import random, os
from hashlib import sha1
from random import randrange
flag=b''
x = bytes_to_long(flag)
def gen_key():
while True:
q = getPrime(160)
p = 2 * getPrime(1024-160) * q+1
if isPrime(p):
break
h = random.randint(1, p - 1)
g = powmod(h,(p-1)//q, p)
y=pow(g,x,p)
return p,q,g,y
def cry():
a =
p = getPrime(512)
q = getPrime(512)
d = getPrime(280)
n = p * q
e = inverse(d, (p - 1) * (q - 1))
c = pow(a, e, n)
return n,e,c
p,q,g,y=gen_key()
k1 = random.randint(1, q-1)
h1 = bytes_to_long(sha1(os.urandom(20)).digest())
r1 = pow(g, k1, p) % q
s1 = ((h1 + x*r1) * invert(k1, q))% q
n,e,c= cry()
a=
b= 17474742587088593627
k2 = a*k1 + b
h2 = bytes_to_long(sha1(os.urandom(20)).digest())
r2 = pow(g, k2, p) % q
s2 = ((h2 + x*r2) * invert(k2, q)) % q
print(n,e,c)
print(p,q,g,y)
print("h1:%s r1:%s s1:%s"%(h1,r1,s1))
print("h2:%s r2:%s s2:%s"%(h2,r2,s2))
1.txt:
n = 98871082998654651904594468693622517613869880791884929588100914778964766348914919202255397776583412976785216592924335179128220634848871563960167726280836726035489482233158897362166942091133366827965811201438682117312550600943385153640907629347663140487841016782054145413246763816202055243693289693996466579973
e = 76794907644383980853714814867502708655721653834095293468287239735547303515225813724998992623067007382800348003887194379223500764768679311862929538017193078946067634221782978912767213553254272722105803768005680182504500278005295062173004098796746439445343896868825218704046110925243884449608326413259156482881
c = 13847199761503953970544410090850216804358289955503229676987212195445226107828814170983735135692611175621170777484117542057117607579344112008580933900051471041224296342157618857321522682033260246480258856376097987259016643294843196752685340912823459403703609796624411954082410762846356541101561523204985391564
p= 161310487790785086482919800040790794252181955976860261806376528825054571226885460699399582301663712128659872558133023114896223014064381772944582265101778076462675402208451386747128794418362648706087358197370036248544508513485401475977401111270352593919906650855268709958151310928767086591887892397722958234379
q= 1115861146902610160756777713087325311747309309771
g= 61073566757714587321114447684333928353300944355112378054603585955730395524359123615359185275743626350773632555967063692889668342544616165017003197599818881844811647270423070958521148291118914198811187731689123176313367399492561288350530256722898205674043032421874788802819858438796795768177550638273020791962
y= 23678147495254433946472657196764372220306841739888385605070426528738230369489739339976134564575544246606937803367113623097260181789372915552172469427842482448570540429192377881186772226796452797182435452490307834205012154495575570994963829345053331967442452842152258650027916313982835119514473311305158299360
(h1, r1, s1) = 535874494834828755542711401117152397489711233142, 117859946800380767356190121030392492081340616512, 26966646740134065096660259687229179143947213779
(h2, r2, s2) = 236574518096866758760287021848258048065293279716, 863199000523521111517835459866422731857447792677, 517924607931342012033031470185302567344725962419
看一眼cry(),d为280bit,n为1024bit,d大概为
n
0.273
n^{0.273}
n0.273,wiener的界限为
1
3
n
1
4
\frac{1}{3}n^{\frac{1}{4}}
31n41,显然超过了wiener的界,而题目名为not_wiener,那就是boneh and durfee了,boneh and durfee的界限为
n
0.292
n^{0.292}
n0.292,刚好在其范围内。
简单设置一下参数,设置delta = .273,m = 7
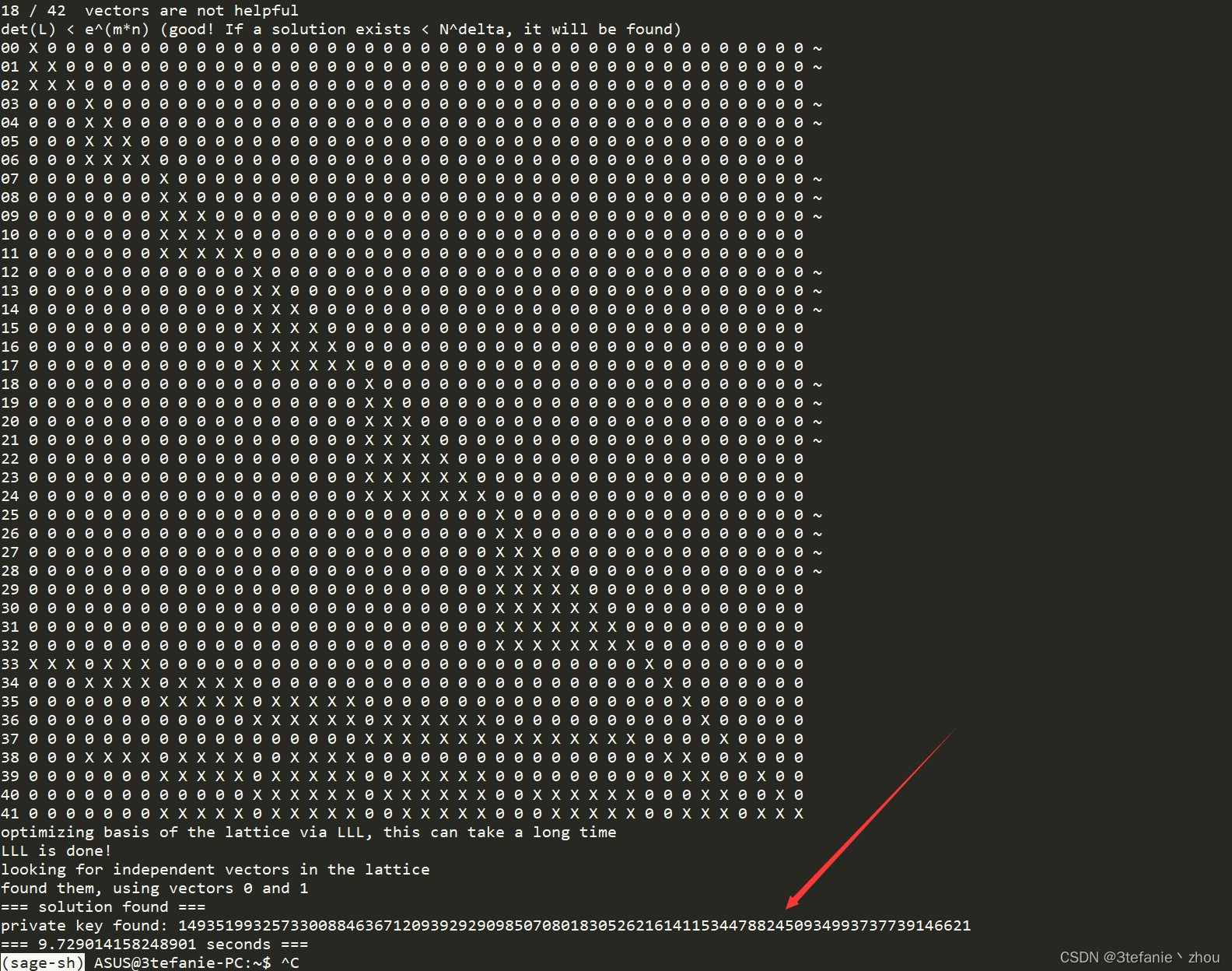
最后带入跑出来的d以及已知的n和c计算得到a
n = 98871082998654651904594468693622517613869880791884929588100914778964766348914919202255397776583412976785216592924335179128220634848871563960167726280836726035489482233158897362166942091133366827965811201438682117312550600943385153640907629347663140487841016782054145413246763816202055243693289693996466579973
e = 76794907644383980853714814867502708655721653834095293468287239735547303515225813724998992623067007382800348003887194379223500764768679311862929538017193078946067634221782978912767213553254272722105803768005680182504500278005295062173004098796746439445343896868825218704046110925243884449608326413259156482881
c = 13847199761503953970544410090850216804358289955503229676987212195445226107828814170983735135692611175621170777484117542057117607579344112008580933900051471041224296342157618857321522682033260246480258856376097987259016643294843196752685340912823459403703609796624411954082410762846356541101561523204985391564
d = 1493519932573300884636712093929290985070801830526216141153447882450934993737739146621
a = pow(c,d,n)
print(a)
#a = 24601959430759983424400804734518943158892550216065342062971649989571838687333
另外一部分,看上去和DSA差不多,主要是等式的变换
此时我们已知
p
,
q
,
g
,
y
,
h
1
,
h
2
,
r
1
,
r
2
,
s
1
,
s
2
p,q,g,y,h_1,h_2,r_1,r_2,s_1,s_2
p,q,g,y,h1,h2,r1,r2,s1,s2,以及有如下等式
s
1
=
(
h
1
+
x
∗
r
1
)
∗
k
1
−
1
m
o
d
q
(
1
)
s_1 = (h_1+x*r_1)*k_1^{-1} \space mod \space q \hspace{2.5cm}(1)
s1=(h1+x∗r1)∗k1−1 mod q(1)
s
2
=
(
h
2
+
x
∗
r
2
)
∗
k
2
−
1
m
o
d
q
(
2
)
s_2 = (h_2+x*r_2)*k_2^{-1} \space mod \space q \hspace{2.5cm}(2)
s2=(h2+x∗r2)∗k2−1 mod q(2)
r
1
=
(
g
k
1
m
o
d
p
)
m
o
d
q
r_1 = (g^{k_1} \space mod \space p) \space mod \space q
r1=(gk1 mod p) mod q
r
2
=
(
g
k
2
m
o
d
p
)
m
o
d
q
r_2 = (g^{k_2} \space mod \space p) \space mod \space q
r2=(gk2 mod p) mod q
k
2
=
a
∗
k
1
+
b
k_2 = a*k_1+b
k2=a∗k1+b
我们的目的是求出x,但是等式中的k1和k2也是未知的,那么我们就没办法直接求x了。因此我们可以参照DSA,先消除关于x的式子
对于式1,乘上
k
1
r
2
k_1r_2
k1r2,得到
s
1
k
1
r
2
=
r
2
(
h
1
+
x
∗
r
1
)
m
o
d
q
s_1k_1r_2 = r_2(h_1+x*r_1) \space mod \space q
s1k1r2=r2(h1+x∗r1) mod q
对于式2,乘上
k
2
r
1
k_2r_1
k2r1,得到
s
2
k
2
r
1
=
r
1
(
h
2
+
x
∗
r
2
)
m
o
d
q
s_2k_2r_1 = r_1(h_2+x*r_2) \space mod \space q
s2k2r1=r1(h2+x∗r2) mod q
将
k
2
=
a
∗
k
1
+
b
k_2 = a*k_1+b
k2=a∗k1+b带入
s
2
(
a
∗
k
1
+
b
)
r
1
=
r
1
(
h
2
+
x
∗
r
2
)
m
o
d
q
s_2(a*k_1+b)r_1 = r_1(h_2+x*r_2) \space mod \space q
s2(a∗k1+b)r1=r1(h2+x∗r2) mod q
两式相减消除x,得到
s
1
k
1
r
2
−
s
2
(
a
∗
k
1
+
b
)
r
1
=
r
2
h
1
−
r
1
h
2
m
o
d
q
s_1k_1r_2-s_2(a*k_1+b)r_1=r_2h_1-r_1h_2 \space mod \space q
s1k1r2−s2(a∗k1+b)r1=r2h1−r1h2 mod q
s
1
k
1
r
2
−
s
2
a
k
1
r
1
−
s
2
b
r
1
=
r
2
h
1
−
r
1
h
2
m
o
d
q
s_1k_1r_2-s_2ak_1r_1-s_2br_1 = r_2h_1-r_1h_2 \space mod \space q
s1k1r2−s2ak1r1−s2br1=r2h1−r1h2 mod q
此时x已经消除,我们的目的是求出k1
再化简一下,得到
k
1
(
s
1
r
2
−
s
2
a
r
1
)
=
r
2
h
1
−
r
1
h
2
+
s
2
b
r
1
m
o
d
q
k_1(s_1r_2-s_2ar_1) = r_2h_1-r_1h_2+s_2br_1 \space mod \space q
k1(s1r2−s2ar1)=r2h1−r1h2+s2br1 mod q
将
k
1
k_1
k1移到左边
k
1
=
(
r
2
h
1
−
r
1
h
2
+
s
2
b
r
1
)
∗
(
s
1
r
2
−
s
2
a
r
1
)
−
1
m
o
d
q
k_1 = (r_2h_1-r_1h_2+s_2br_1)*(s_1r_2-s_2ar_1)^{-1} \space mod \space q
k1=(r2h1−r1h2+s2br1)∗(s1r2−s2ar1)−1 mod q
此时式子中的变量都已知,带入即可计算出
k
1
k_1
k1
解出k1,然后带入到
s
1
=
(
h
1
+
x
∗
r
1
)
∗
k
1
−
1
m
o
d
q
s_1 = (h_1+x*r_1)*k_1^{-1} \space mod \space q
s1=(h1+x∗r1)∗k1−1 mod q
化简一下,得到x的等式
x
=
(
s
1
∗
k
1
−
h
1
)
∗
r
1
−
1
m
o
d
q
x = (s_1*k_1-h_1)*r_1^{-1} \space mod \space q
x=(s1∗k1−h1)∗r1−1 mod q
最后转换一下x即可得到flag
exp如下:
#sage
p= 161310487790785086482919800040790794252181955976860261806376528825054571226885460699399582301663712128659872558133023114896223014064381772944582265101778076462675402208451386747128794418362648706087358197370036248544508513485401475977401111270352593919906650855268709958151310928767086591887892397722958234379
q= 1115861146902610160756777713087325311747309309771
g= 61073566757714587321114447684333928353300944355112378054603585955730395524359123615359185275743626350773632555967063692889668342544616165017003197599818881844811647270423070958521148291118914198811187731689123176313367399492561288350530256722898205674043032421874788802819858438796795768177550638273020791962
y= 23678147495254433946472657196764372220306841739888385605070426528738230369489739339976134564575544246606937803367113623097260181789372915552172469427842482448570540429192377881186772226796452797182435452490307834205012154495575570994963829345053331967442452842152258650027916313982835119514473311305158299360
(h1, r1, s1) = 535874494834828755542711401117152397489711233142, 117859946800380767356190121030392492081340616512, 26966646740134065096660259687229179143947213779
(h2, r2, s2) = 236574518096866758760287021848258048065293279716, 863199000523521111517835459866422731857447792677, 517924607931342012033031470185302567344725962419
a= 24601959430759983424400804734518943158892550216065342062971649989571838687333
b= 17474742587088593627
k1 = (r2*h1-r1*h2+s2*b*r1)*inverse_mod(s1*r2-s2*a*r1,q)%q
x = (s1*k1-h1)*inverse_mod(r1,q)%q
flag = bytes.fromhex(hex(x)[2:])
print(flag)
#l1near_k1s_unsafe
【所有远游,都是为了重逢。】





![编译原理2.3习题 语法制导分析[C++]](https://img-blog.csdnimg.cn/direct/d95a220fe7394240a247d6392c8c10d5.png)