Tarjan 算法（超详细！！）

news2024/9/27 15:35:47

推荐在 cnblogs 上阅读

Tarjan 算法

前言

说来惭愧，这个模板仅是绿的算法至今我才学会。

我还记得去年 CSP2023 坐大巴路上拿着书背 Tarjan 的模板。虽然那年没有考连通分量类似的题目。

现在做题遇到了 Tarjan，那么，重学，开写！

另，要想学好此算法的第一件事——膜拜 Tarjan 爷爷。

Tarjan 算法到底是什么

其实广义上有许多算法都是 Tarjan 发明的（大名鼎鼎的 Link-Cut-Tree 正是出自他手），而本文介绍的是可以解决图中强连通分量的算法。

也就是狭义的 Tarjan 算法。

什么是强连通分量

对于一个图 $G$ 来说，一个字图中，任意两点都可以彼此到达（存在路径），这个子图就称为图 $G$ 的强连通分量。特别地，一个点也是一个强连通分量。

算法思路

Tarjan 是基于 DFS 实现的，走过的边会形成一棵搜索树。可以看作是原图删去一些边留下来而形成的。

看个图吧：

如果我们把抛弃的边分为三个大类，可以分为：

横叉边（红）
前向边（黄）
后向边（蓝）

上图把抛弃的边画出来就是这样了：

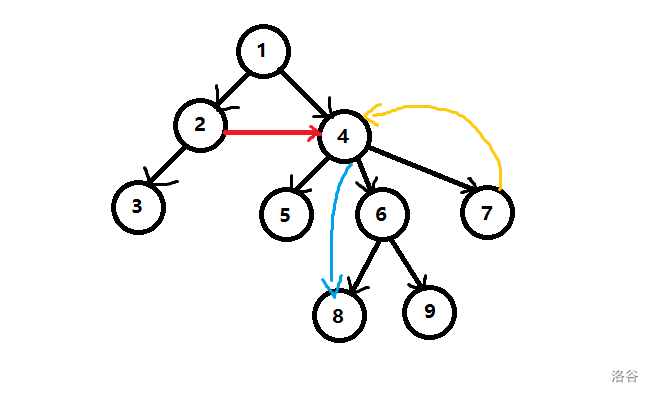
容易发现，能够构成环的只有前向边。而我们所需要得到的连通分量，正需要环。

我们怎么知道 DFS 到什么时候是一条前向边呢？

我们可以在 DFS 过程中给每个点打一个时间戳（实际上就是 DFS 序， dfn[x]=++cnt），如此，当我们遍历某节点的儿子 $v$ 时， $v$ 是一个已访问过的节点，那么我们找到了后向边。

如何维护？——用两个数组

dfn[i]：储存时间戳。
low[i]：储存 $i$ 点可以访问到的最高祖先的 dfn 值（因为 DFS 序由小到大，所以储存的数越小、表示 $i$ 点访问祖先能力越强）。

特殊地，一个点访问祖先的能力再差，也可以访问到自己。

代码实现

code

int dfn[MAXN],low[MAXN],tim;
bool vis[MAXN];
int ans;
stack<int> st;
int belong[MAXN];
vector<int> G[MAXN];
void tarjan(int x)
{
    dfn[x]=low[x]=++tim;
    st.push(x);
    vis[x]=1;
    for(int i=hd[x];i;i=lt[i])
    {
        int v=en[i];
        if(!dfn[v])
        {
            tarjan(v);
            low[x]=min(low[x],low[v]);
        }
        else if(vis[v]) // 此时找到后向边，不着急操作，等待回溯以后在操作
            low[x]=min(low[x],dfn[v]);
    }
    if(dfn[x]==low[x]) // 这是根节点独有的性质
    {
        ++ans; // 看看目前已经是第几个强连通分量了
        int top;
        do
        {
            top=st.top();st.pop();
            vis[top]=0;
            belong[top]=ans; // belong[] : 某节点属于那个强连通分量
            G[ans].push_back(top); // 强连通分量有哪些成员节点。
        } while (top!=x);
    }
}

P1726 上白泽慧音

题目要求：求出最大强连通分量、并输出其成员。如数量相同，输出最小的成员集合。

此题目中，belong[] 就不需要了，存成员是必要的；按字典序输出的话，把成员丢进优先队列带走，秒了！

code

#include<bits/stdc++.h>
using namespace std;

#define int long long

const int MAXN=2e5+5;

int n,m;
int dfn[MAXN],low[MAXN],tim;
bool vis[MAXN];
int ans;
stack<int> st;
int belong[MAXN];
int su,hd[MAXN],lt[MAXN],en[MAXN];
priority_queue<int,vector<int>,greater<int>> G[MAXN];
struct node
{
    int id,sz,val;
}p[MAXN];

void add(int u,int v)
{
    en[++su]=v,lt[su]=hd[u],hd[u]=su;
}

void tarjan(int x)
{
    dfn[x]=low[x]=++tim;
    st.push(x);
    vis[x]=1;
    for(int i=hd[x];i;i=lt[i])
    {
        int v=en[i];
        if(!dfn[v])
        {
            tarjan(v);
            low[x]=min(low[x],low[v]);
        }
        else if(vis[v])
            low[x]=min(low[x],dfn[v]);
    }
    if(dfn[x]==low[x])
    {
        ++ans;
        p[ans].id=ans;
        p[ans].val=st.top();
        int top;
        do
        {
            top=st.top();st.pop();
            vis[top]=0;
            belong[top]=ans;
            p[ans].sz++;
            G[ans].push(top);
        } while (top!=x);
    }
}

signed main()
{
    scanf("%lld%lld",&n,&m);
    for(int i=1,u,v,w;i<=m;i++)
    {
        scanf("%lld%lld%lld",&u,&v,&w);
        add(u,v);
        if(w==2) add(v,u);
    }
  
    for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);

    sort(p+1,p+ans+1,[](node x,node y){
        return x.sz==y.sz?x.val<y.val:x.sz>y.sz;
    });

    printf("%lld\n",p[1].sz);
    while (!G[p[1].id].empty())
    {
        printf("%lld ",G[p[1].id].top());
        G[p[1].id].pop();
    }
  
    return 0;
}