5.4 如何高效解决接雨水问题

本文对应的力扣题目：

42.接雨水

说白了就是用一个数组表示一个条形图，问你这个条形图最多能接多少水，函数签名如下：

int trap(int[] height);

5.4.1 核心思路

暴力算法：

int trap(vector<int>& height) {
    int n = height.size();
    int ans = 0;
    for (int i = 1; i < n - 1; i++) {
        int l_max = 0, r_max = 0;
        // 找右边最高的柱子
        for (int j = i; j < n; j++)
            r_max = max(r_max, height[j]);
        // 找左边最高的柱子
        for (int j = i; j >= 0; j--)
            l_max = max(l_max, height[j]);
        // 计算能够装的水
        ans += min(l_max, r_max) - height[i];
    }
    return ans;
}

5.4.2 备忘录优化

预先把这两个数组计算好，即可避免重复计算：

int trap(vector<int>& height) {
    if (height.empty()) return 0;
    int n = height.size();
    int ans = 0;
    // 数组充当备忘录
    vector<int> l_max(n), r_max(n);
    // 初始化 base case
    l_max[0] = height[0];
    r_max[n - 1] = height[n - 1];
    // 从左向右计算 l_max
    for (int i = 1; i < n; i++)
        l_max[i] = max(height[i], l_max[i - 1]);
    // 从右向左计算 r_max
    for (int i = n - 2; i >= 0; i--) 
        r_max[i] = max(height[i], r_max[i + 1]);
    // 计算答案
    for (int i = 1; i < n - 1; i++) 
        ans += min(l_max[i], r_max[i]) - height[i];
    return ans;
}

5.4.3 双指针解法

int trap(vector<int>& height) {
    if (height.empty()) return 0;
    int n = height.size();
    int left = 0, right = n - 1;
    int ans = 0;
    
    int l_max = height[0];
    int r_max = height[n - 1];
    
    while (left <= right) {
        l_max = max(l_max, height[left]);
        r_max = max(r_max, height[right]);
        
        // ans += min(l_max, r_max) - height[i]
        if (l_max < r_max) {
            ans += l_max - height[left];
            left++; 
        } else {
            ans += r_max - height[right];
            right--;
        }
    }
    return ans;
}

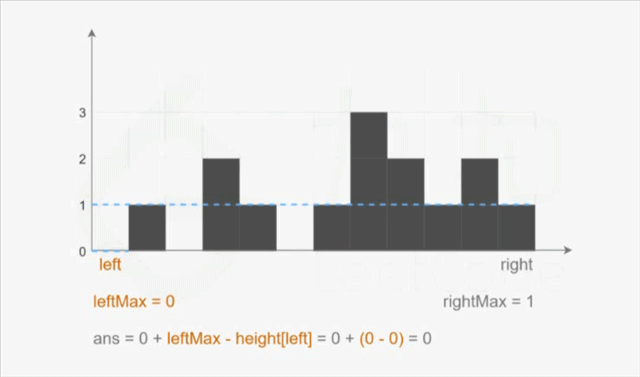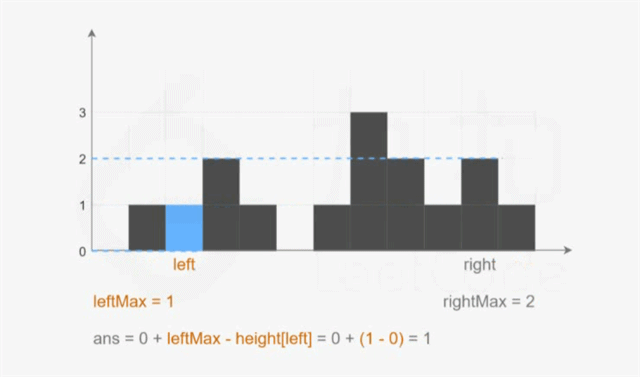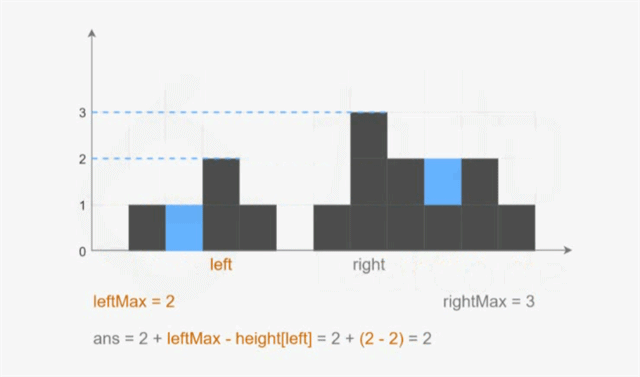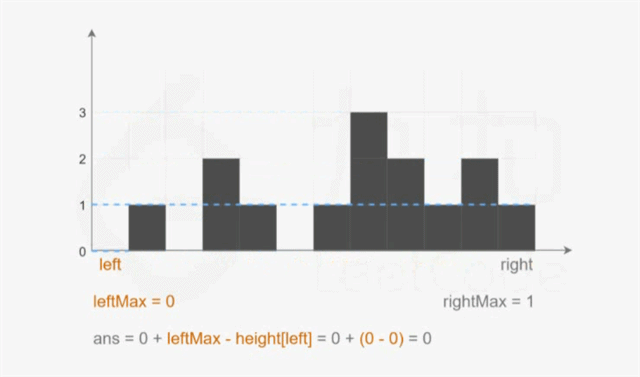
var trap = function(height){
    // 初始化能接雨水量
    let ans = 0;
    // 初始化两个指针，左边为0，右边为柱高长度-1
    let left = 0, right = height.length - 1;
    // 初始化两边存储最大值
    let leftMax = 0, rightMax = 0;
    // 当两个指针没有相遇的时候
    while(left < right){
        // 更新两边存储最大值
        leftMax = Math.max(leftMax, height[left]);
        rightMax = Math.max(rightMax, height[right]);
        // 如果 左边柱子高度 小于 右边
        if(height[left] < height[right]){
            // 下标 left 处能接的雨水量 = 左边存储的最大值 - 左边柱子高度
            ans += leftMax - height[left];
            // 移动左指针
            ++left;
        }else{
            ans += rightMax -  height[right];
            --right;
        }
    }
    return ans;
}

繁琐问题必有猥琐解法，记录简单处理问题的逻辑，就能掌握规律！