1.决定下一步做什么

问题：
假如，在你得到你的学习参数以后，如果你要将你的假设函数放到一组
新的房屋样本上进行测试，假如说你发现在预测房价时产生了巨大的误差，现在你的问题是要想改进这个算法，接下来应该怎么办？
解决思路：
一种办法是使用更多的训练样本。具体来讲，也许你能想到通过电话调查或上门调查来获取更多的不同的房屋出售数据。但是实际上特别多的数据是没有太大用处的。
另一个方法，你也许能想到的是尝试选用更少的特征集。因此如果你有一系列特征，比如𝑥1, 𝑥2, 𝑥3等等。也许有很多特征，也许你可以花一点时间从这些特征中仔细挑选一小部分来防止过拟合。或者也许你需要用更多的特征，也许目前的特征集，对你来讲并不是很有帮助。
获得更多的训练实例——通常是有效的，但代价较大，下面的方法也可能有效，可考虑先采用下面的几种方法。
1.尝试减少特征的数量
2.尝试获得更多的特征
3.尝试增加多项式特征
4.尝试减少正则化程度𝜆
5.尝试增加正则化程度𝜆

2.评估一个假设

用算法来评估假设函数，并以此为基础考虑如何避免过拟合和欠拟合问题。
选择参量来使训练误差最小化并不一定是好事，因为可能会出现过拟合的情况。
如何判定一个假设函数过拟合？
可以对假设函数ℎ(𝑥)进行画图，然后观察图形趋势，但对于特征变量不止一个的这种一般情况，还有像有很多特征变量的问题，想要通过画出假设函数来进行观察，就会变得很难甚至是不可能实现。为了检验算法是否过拟合，我们将数据分成训练集和测试集，通常用 70%的数据作为训练集，用剩下 30%的数据作为测试集。很重要的一点是训练集和测试集均要含有各种类型的数据，通常我们要对数据进行“洗牌”，然后再分成训练集和测试集。

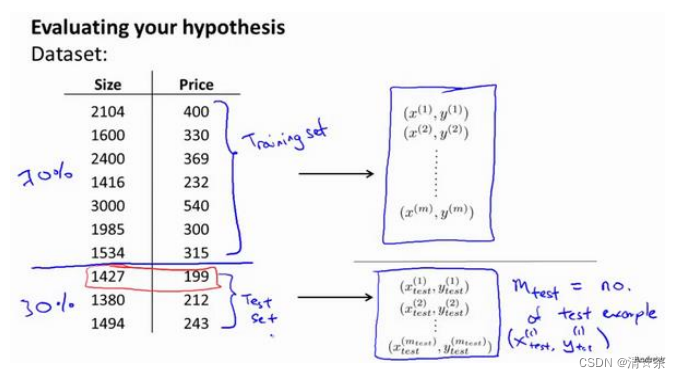
测试集评估在通过训练集让我们的模型学习得出其参数后，对测试集运用该模型，我们有两种方式计算误差：
1.对于线性回归模型，我们利用测试集数据计算代价函数𝐽
2.对于逻辑回归模型，我们除了可以利用测试数据集来计算代价函数外：

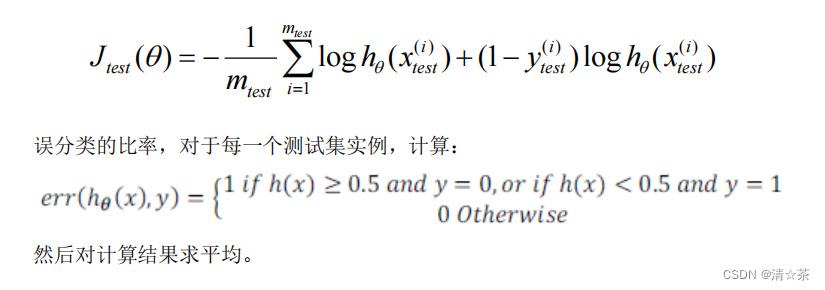
3.模型选择和交叉验证集

假设我们要在 10 个不同次数的二项式模型之间进行选择：

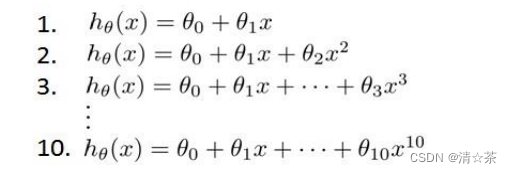
显然越高次数的多项式模型越能够适应训练集，但是适应训练集并不一定能推广到一般情况，只需要选择更能适应一般情况的模型，需要使用交叉验证集来帮助选择模型。
即：使用 60%的数据作为训练集，使用 20%的数据作为交叉验证集，使用 20%的数据作为测试。

模型选择的方法为：

1. 使用训练集训练出 10 个模型
2. 用 10 个模型分别对交叉验证集计算得出交叉验证误差（代价函数的值）
3. 选取代价函数值最小的模型
4. 用步骤 3 中选出的模型对测试集计算得出推广误差（代价函数的值）

代价函数：

模型选择是指在多个候选模型中选择一个最佳模型的过程。在机器学习中，不同的模型有不同的适用场景和性能表现，因此需要根据具体情况选择最适合的模型。常用的模型选择方法包括交叉验证、网格搜索等。

交叉验证集是用于评估模型泛化能力的数据集，它通常被分为训练集和测试集。训练集用于训练模型，测试集用于评估模型的泛化能力。通过将数据集分成多个子集，并在不同的子集上重复进行训练和测试，可以更准确地评估模型的性能，并选择最佳的模型参数。

在模型选择过程中，可以使用交叉验证集来评估不同模型的性能表现，并选择最佳的模型。常用的交叉验证方法包括k折交叉验证、留一法等。这些方法可以帮助我们评估模型的泛化误差，并选择最佳的模型参数，从而提高模型的性能表现。

4.诊断偏差和方差

问题：如果算法的表现不理想，那么多半是出现两种情况：要么是偏差比较大，要么是方差比较大。换句话说，出现的情况要么是欠拟合，要么是过拟
合问题。那么这两种情况，哪个和偏差有关，哪个和方差有关，或者是不是和两个都有关？

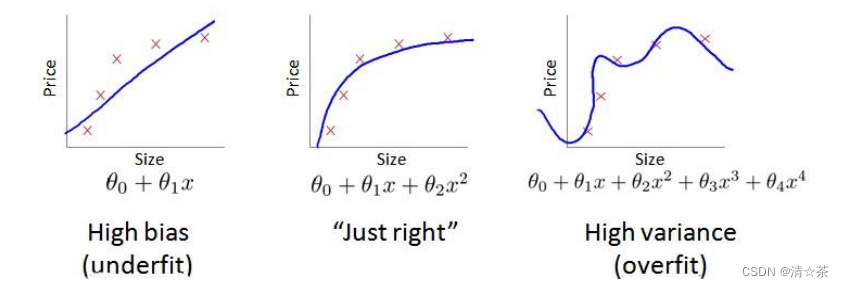
通常会通过将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图表上来帮助分析：


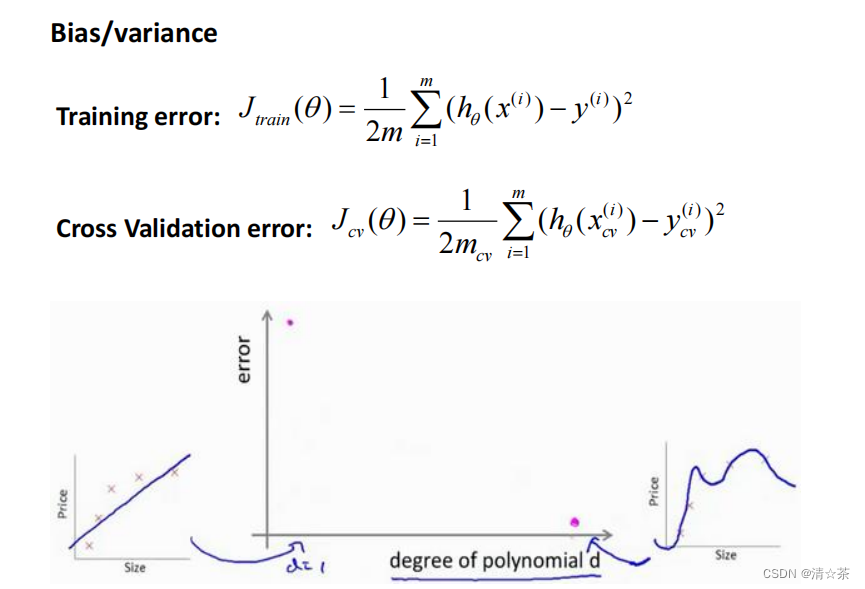
对于训练集，当 𝑑 较小时，模型拟合程度更低，误差较大；随着 𝑑 的增长，拟合程度提高，误差减小。
对于交叉验证集，当 𝑑 较小时，模型拟合程度低，误差较大；但是随着 𝑑 的增长，误差呈现先减小后增大的趋势，转折点是我们的模型开始过拟合训练数据集的时候。
根据图表可知：
训练集误差和交叉验证集误差近似时：偏差/欠拟合
交叉验证集误差远大于训练集误差时：方差/过拟合

5.正则化和偏差/方差

正则化可以通过调整模型参数或增加惩罚项来减小模型的复杂度，从而减小模型的偏差和方差。例如，L1正则化和L2正则化可以通过约束模型参数的绝对值或范数来减小模型的复杂度，dropout可以在训练过程中随机丢弃一部分神经元，从而使得模型不会过于依赖某一些神经元。
在训练模型的过程中，会使用正则化来防止过拟合，但是可能正则化过高或者过低，所以要选择合适的 λ。

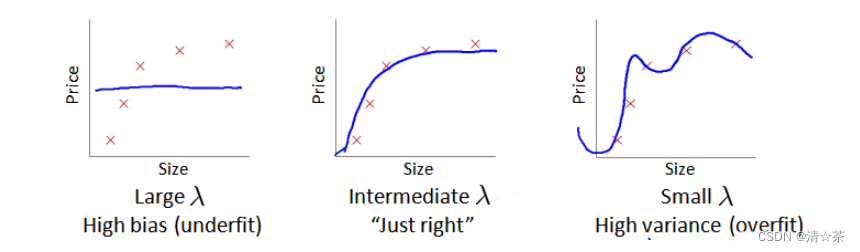
我们选择一系列的想要测试的 𝜆 值，通常是 0-10 之间的呈现 2 倍关系的值（如：0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10共 12 个）。我们同样把数据分为训练集、交叉验证集和测试集。

选择𝜆的方法为：
1.使用训练集训练出 12 个不同程度正则化的模型
2.用 12 个模型分别对交叉验证集计算的出交叉验证误差
3.选择得出交叉验证误差最小的模型
4.运用步骤 3 中选出模型对测试集计算得出推广误差，我们也可以同时将训练集和交叉验证集模型的代价函数误差与 λ 的值绘制在一张图表上：

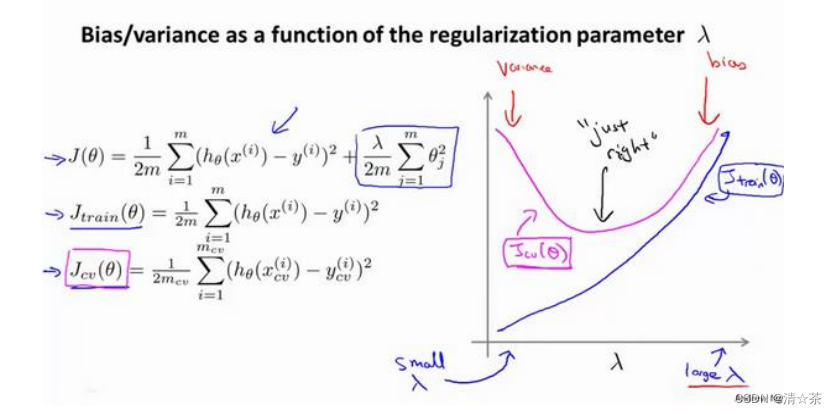
• 当 𝜆 较小时，训练集误差较小（过拟合）而交叉验证集误差较大
• 随着 𝜆 的增加，训练集误差不断增加（欠拟合），而交叉验证集误差则是先减小后增加

6.学习曲线

学习曲线是学习算法的一个很好的合理检验（sanity check）。学习曲线是将训练集误差和交叉验证集误差作为训练集实例数量（𝑚）的函数绘制的图表。
即，如果我们有 100 行数据，我们从 1 行数据开始，逐渐学习更多行的数据。思想是：当训练较少行数据的时候，训练的模型将能够非常完美地适应较少的训练数据，但是训练出来的模型却不能很好地适应交叉验证集数据或测试集数据。

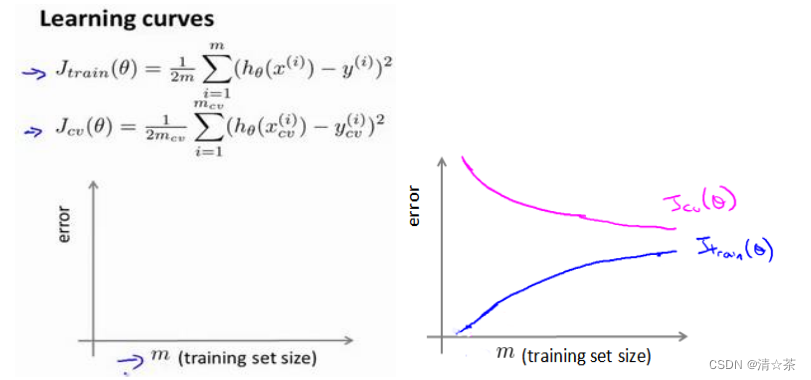
但是高偏差/欠拟合的情况下，增加数据到训练集不一定是有效果的。
如何利用学习曲线识别高方差/过拟合？
假设我们使用一个非常高次的多项式模型，并且正则化非常小，可以看出，当交叉验证集误差远大于训练集误差时，往训练集增加更多数据可以提高模型的效果。

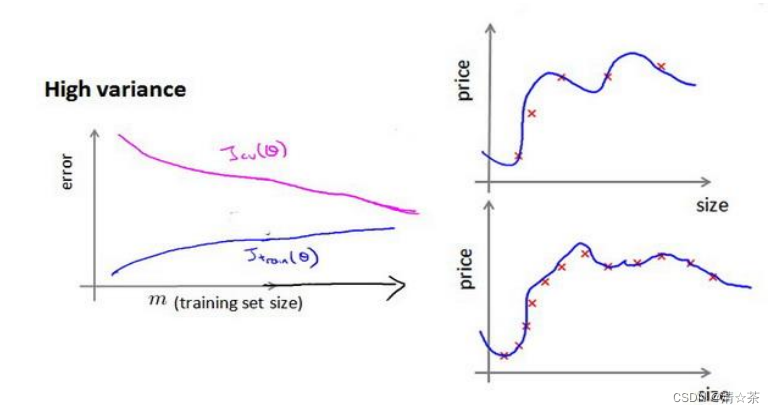
在高方差/过拟合的情况下，增加更多数据到训练集可能可以提高算法效果。

学习曲线是一种用于评估机器学习模型性能的工具，它展示了模型在训练过程中的表现。学习曲线可以通过绘制训练集误差和验证集误差随训练集大小的变化曲线来生成。

学习曲线通常具有以下特点：

随着训练集大小的增加，训练集误差和验证集误差都会逐渐减小。
如果训练集大小增加到一定程度后，训练集误差和验证集误差会趋于稳定，这时模型已经充分学习了数据集中的信息，进一步增加训练集大小对提高模型性能的帮助不大。
如果模型存在过拟合或欠拟合问题，学习曲线会有不同的表现。过拟合会导致训练集误差和验证集误差之间的差距逐渐增大，而欠拟合会导致两者之间的差距保持较大。
学习曲线可以用于诊断模型的性能问题，以及指导模型选择和参数调整。通过观察学习曲线的形状和动态变化，可以了解模型是否过拟合或欠拟合，以及是否需要调整模型的超参数。此外，学习曲线还可以用于比较不同模型之间的性能表现，从而选择最优的模型。

7.综合总结

问题：怎样评价一个学习算法，了解了模型选择问题，偏差和方差的问题。诊断法则怎样帮助我们判断，哪些方法可能有助于改进学习算法的效果，而哪些可能是徒劳的呢？
在什么情况下应该怎样选择：

1. 获得更多的训练实例——解决高方差
2. 尝试减少特征的数量——解决高方差
3. 尝试获得更多的特征——解决高偏差
4. 尝试增加多项式特征——解决高偏差
5. 尝试减少正则化程度 λ——解决高偏差
6. 尝试增加正则化程度 λ——解决高方差
   神经网络的方差和偏差：
   
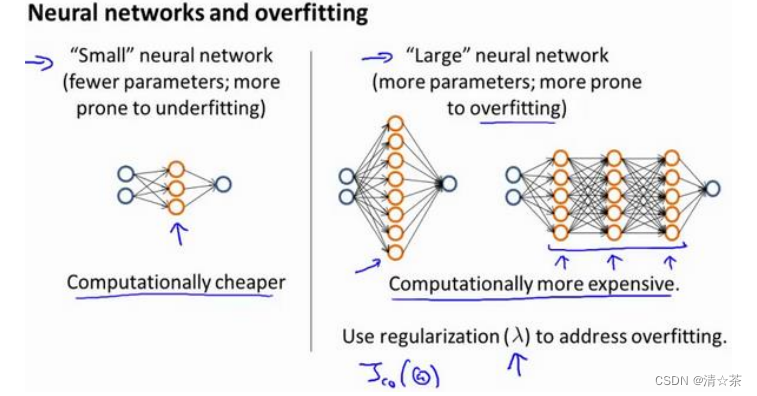
   使用较小的神经网络，类似于参数较少的情况，容易导致高偏差和欠拟合，但计算代价较小使用较大的神经网络，类似于参数较多的情况，容易导致高方差和过拟合，虽然计算代价比较大，但是可以通过正则化手段来调整而更加适应数据。
   通常选择较大的神经网络并采用正则化处理会比采用较小的神经网络效果要好。
   对于神经网络中的隐藏层的层数的选择，通常从一层开始逐渐增加层数，为了更好地作选择，可以把数据分为训练集、交叉验证集和测试集，针对不同隐藏层层数的神经网络训练神经网络， 然后选择交叉验证集代价最小的神经网络。