使用torch实现RNN

news2024/9/25 17:11:10

在实验室的项目遇到了困难，弄不明白LSTM的原理。到网上搜索，发现LSTM是RNN的变种，那就从RNN开始学吧。

带隐藏状态的RNN可以用下面两个公式来表示：

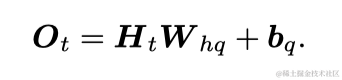
可以看出，一个RNN的参数有W_xh，W_hh，b_h，W_hq，b_q和H(t)。其中H(t)是步数的函数。

参考的文章考虑了这样一个问题，对于x轴上的一列点，有一列sin值，我们想知道它对应的cos值，但是即使sin值相同，cos值也不同，因为输出结果不仅依赖于当前的输入值sinx，还依赖于之前的sin值。这时候可以用RNN来解决问题

用到的核心函数：torch.nn.RNN() 参数如下：

input_size – 输入x的特征数量。
hidden_size – 隐藏层的特征数量。
num_layers – RNN的层数。
nonlinearity – 指定非线性函数使用tanh还是relu。默认是tanh。
bias – 如果是False，那么RNN层就不会使用偏置权重 bihbih和bhhbhh,默认是True
batch_first – 如果True的话，那么输入Tensor的shape应该是[batch_size, time_step, feature],输出也是这样。
dropout – 如果值非零，那么除了最后一层外，其它层的输出都会套上一个dropout层。
bidirectional – 如果True，将会变成一个双向RNN，默认为False。

下面是代码：

 1 # encoding:utf-8
 2 import torch
 3 import numpy as np
 4 import matplotlib.pyplot as plt  # 导入作图相关的包
 5 from torch import nn
 6 
 7 
 8 # 定义RNN模型
 9 class Rnn(nn.Module):
10     def __init__(self, INPUT_SIZE):
11         super(Rnn, self).__init__()
12 
13         # 定义RNN网络,输入单个数字.隐藏层size为[feature, hidden_size]
14         self.rnn = nn.RNN(
15                 input_size=INPUT_SIZE,
16                 hidden_size=32,
17                 num_layers=1,
18                 batch_first=True  # 注意这里用了batch_first=True 所以输入形状为[batch_size, time_step, feature]
19                 )
20         # 定义一个全连接层,本质上是令RNN网络得以输出
21         self.out = nn.Linear(32, 1)
22 
23     # 定义前向传播函数
24     def forward(self, x, h_state):
25         # 给定一个序列x,每个x.size=[batch_size, feature].同时给定一个h_state初始状态,RNN网络输出结果并同时给出隐藏层输出
26         r_out, h_state = self.rnn(x, h_state)
27         outs = []
28         for time in range(r_out.size(1)):  # r_out.size=[1,10,32]即将一个长度为10的序列的每个元素都映射到隐藏层上.
29             outs.append(self.out(r_out[:, time, :]))  # 依次抽取序列中每个单词,将之通过全连接层并输出.r_out[:, 0, :].size()=[1,32] -> [1,1]
30         return torch.stack(outs, dim=1), h_state  # stack函数在dim=1上叠加:10*[1,1] -> [1,10,1] 同时h_state已经被更新
31 
32 
33 TIME_STEP = 10
34 INPUT_SIZE = 1
35 LR = 0.02
36 
37 model = Rnn(INPUT_SIZE)
38 print(model)
39 
40 loss_func = nn.MSELoss()  # 使用均方误差函数
41 optimizer = torch.optim.Adam(model.parameters(), lr=LR)  # 使用Adam算法来优化Rnn的参数,包括一个nn.RNN层和nn.Linear层
42 
43 h_state = None  # 初始化h_state为None
44 
45 for step in range(300):
46     # 人工生成输入和输出,输入x.size=[1,10,1],输出y.size=[1,10,1]
47     start, end = step * np.pi, (step + 1)*np.pi
48 
49     steps = np.linspace(start, end, TIME_STEP, dtype=np.float32)
50     x_np = np.sin(steps)
51     y_np = np.cos(steps)
52 
53     x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis])
54     y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])
55 
56     # 将x通过网络,长度为10的序列通过网络得到最终隐藏层状态h_state和长度为10的输出prediction:[1,10,1]
57     prediction, h_state = model(x, h_state)
58     h_state = h_state.data  # 这一步只取了h_state.data.因为h_state包含.data和.grad 舍弃了梯度
59     # 反向传播
60     loss = loss_func(prediction, y)
61     optimizer.zero_grad()
62     loss.backward()
63 
64     # 优化网络参数具体应指W_xh, W_hh, b_h.以及W_hq, b_q
65     optimizer.step()
66 
67 # 对最后一次的结果作图查看网络的预测效果
68 plt.plot(steps, y_np.flatten(), 'r-')
69 plt.plot(steps, prediction.data.numpy().flatten(), 'b-')
70 plt.show()

最后一步预测和实际y的结果作图如下：