动态规划系列问题
- 1.打家劫舍问题
- 1.1打家劫舍I
- 1.2打家劫舍II
- 1.3打家劫舍III
- 2.买股票问题
- 2.1买股票的最佳时机
- 2.2买股票的最佳时机II
- 2.3买股票的最佳时机III
- 2.4买股票的最佳时机IV
- 2.5买卖股票的最佳时机含冷冻期
- 2.6买卖股票的最佳时机含手续费
题目解析参考了代码随想录
https://www.programmercarl.com/
1.打家劫舍问题
1.1打家劫舍I
这个题目比较简单，我们每一次递推的时候，只需要考虑选不选当前房子就行
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])（两种情况选最大值即可）
dp[i - 1]表示不选当前房子得到的价值，dp[i - 2] + nums[i]表示选了当前房子得到的价值
class Solution {
public:
int rob(vector<int>& nums) {
if(nums.size() == 1) return nums[0];
vector<int> dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for(int i = 2; i < nums.size(); i++){
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[nums.size() - 1];
}
};
1.2打家劫舍II
这个题目在上一个题目的基础上，将房屋首尾相连了，这个时候的解决方法也很简单，我们动态规划的时候分两种情况考虑，dp1是选择了打劫了第一家房子，dp2是没有选择打劫第一家房子，递推式和上面相同，但是这里dp1和dp2数组的初始化有讲究
dp1[0] = nums[0] ,dp[1] = nums[0] 因为打劫了第一家房子所有不能选择第二家房子和最后一家房子
dp2[0] = 0, dp2[1] = nums[1] 打劫了第二家房子，第一家房子不能后选择，但是最后一间房子可以考虑打劫
代码实现如下：
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
if(n == 1) return nums[0];
if(n == 2) return max(nums[0], nums[1]);
//nums围成了一个圈，所以我们这个时候的dp就可以分两种情况考虑：偷第一户人，和不偷第一户人
vector<int> dp1(n), dp2(n);
//dp1偷第一户人家：那么它不可以偷最后一户人家(所以i<n - 1)
dp1[0] = dp1[1] = nums[0];
for(int i = 2; i < n - 1; i++){
dp1[i] = max(dp1[i - 2] + nums[i], dp1[i - 1]);
}
//dp2不偷第一户人家:那么就可以选择是否偷最后一户人家（所以i<n)
dp2[0] = 0, dp2[1] = nums[1];
for(int i = 2; i < n; i++){
dp2[i] = max(dp2[i - 2] + nums[i], dp2[i - 1]);
}
return max(dp1[n - 2], dp2[n - 1]);
}
};
1.3打家劫舍III
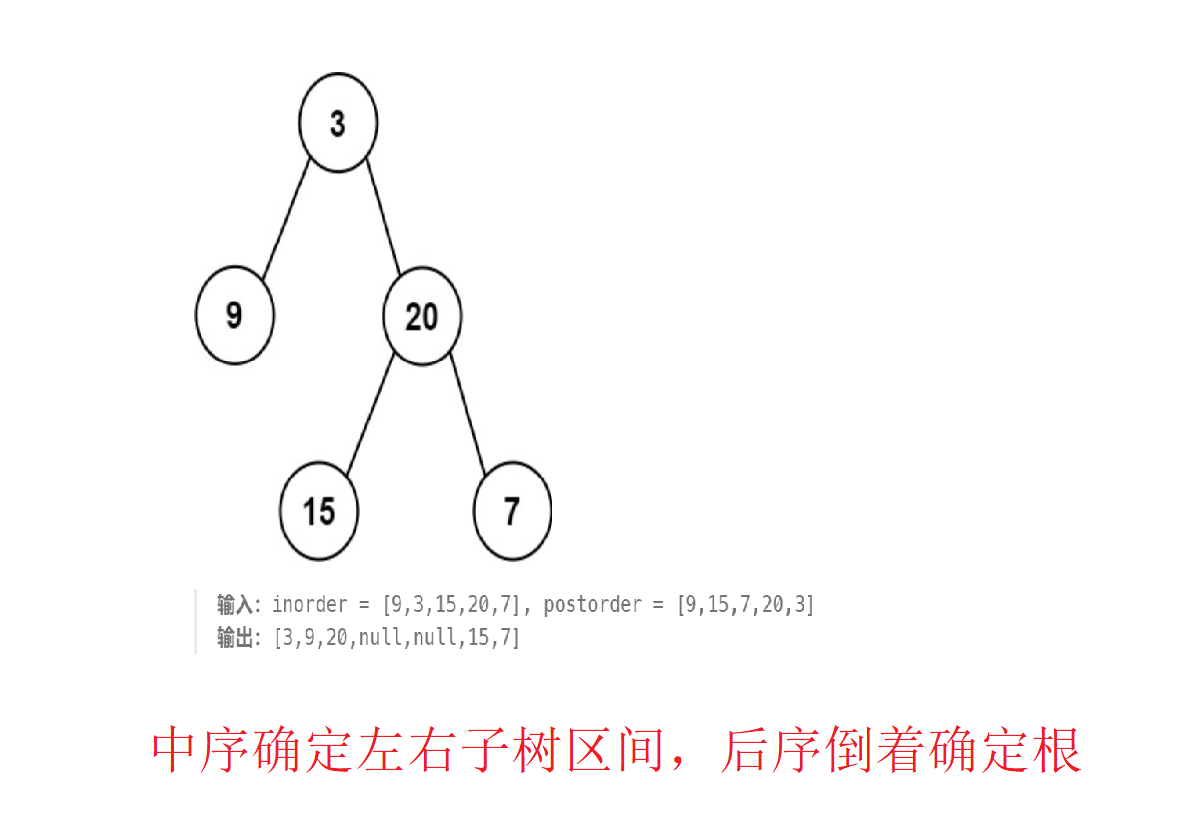
小偷打劫也真的是难啊，从数组变成了二叉树，添加了二叉树遍历的考点，难度又提升了。给出二叉树题目的常见题解，就是暴力递归，得到所有可能结果，为了不超时，暴力递归的时候添加上记忆化的操作。二叉树遍历选择后序遍历，因为是否选择根节点的值取决于其子节点的放返回结果（要想办法选择最大价值）
解法一：递归+记忆化
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<TreeNode* ,int> umap; //记录计算过的结果
//选择后序遍历，需要通过递归函数的返回值来做下一步计算
int rob(TreeNode* root) {
if(root == NULL) return 0;
if(root->left == nullptr && root -> right == nullptr) return root->val;
if(umap[root]) return umap[root];//如果umap里面有记录了，就直接返回
//偷父节点
int val1 = root->val;
if(root->left) val1 += rob(root->left->left) +rob(root->left->right);
if(root->right) val1 += rob(root->right->left) + rob(root->right->right);
//不偷父节点的情况
int val2 = rob(root->left) + rob(root->right);
umap[root] = max(val1, val2);
return max(val1, val2);
}
};
那么动态规划如何实现该题目的求解呢？这里定义dp数组就变得尤为重要了，在本题中，动态规划要结合递归的特性来定义dp，dp为一个大小为2的数组
确定状态转移方程
方法二：动态规划代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int rob(TreeNode* root) {
vector<int> result = robTree(root);
return max(result[0], result[1]);
}
//长度为2的数组，0：不偷，1：偷
vector<int> robTree(TreeNode* cur){
if(cur == NULL) return vector<int>{0, 0};
vector<int> left = robTree(cur->left);
vector<int> right = robTree(cur->right);
//偷cur，那么就不能偷左右节点
int val1 = cur->val + left[0] + right[0];
//不偷cur，那么可以偷也可以不偷左右节点，取最大的情况
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return {val2, val1};
}
};
2.买股票问题
2.1买股票的最佳时机
这个题目，我们可以这样：如果第二天卖出去为正收入，那么就继续考虑第三天再买…如果第二天卖出去为负，那么就更新买入的位置…这个过程中，用一个ans维护卖出获得的最大值
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ans = 0;
int cnt = 0;
if(prices.size() == 1) return ans;
for(int i = 1; i < prices.size(); i++){
cnt += prices[i] - prices[i - 1];
if(cnt < 0){
cnt = 0;
}
ans = max(cnt, ans);
}
return ans;
}
};
2.2买股票的最佳时机II
既然可以多次买入卖出，那么我们只要买入股票第二天卖出是获利的那么就是把利润添加到结果中，只要两天只差(卖出-买入 >0)就买，然后把利润一直++，这样就可以获得最大利润
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ans = 0;
if(prices.size() == 1) return ans;
for(int i = 1; i < prices.size(); i++){
int gap = prices[i] - prices[i - 1];
if(gap > 0) ans += gap;
}
return ans;
}
};
2.3买股票的最佳时机III
当我们只能够买入两次，并且卖出两次（且买入卖出不可以交叉时），我们动态规划的状态如下：
状态定义
状态转移方程
class Solution {
public:
//动态规划过程实现过程
//动态规划过程分为下面四个状态：不持有股票；第一次持有股票；第一次不持有股票；第二次持有股票；第二次不持有股票
int maxProfit(vector<int>& prices) {
if(prices.size() == 0) return 0;
vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
dp[0][1] = -prices[0];
dp[0][3] = -prices[0];
for(int i = 1; i < prices.size(); i++){
dp[i][0] = dp[i - 1][0];//不持有股票
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);//第一次持有股票
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);//第一次卖出股票
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);//第二次持有股票
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);//第二次卖出股票
}
return dp[prices.size() - 1][4];
}
};
2.4买股票的最佳时机IV
当买卖次数由上一题的2两次（买卖至多各两次）变成本题目的k次，我们需要发现交易的规律
定义动态规划数组
递推方程式
代码实现
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
if(prices.size() == 0) return 0;
//奇数次是买入，偶数次是卖出
vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
for(int i = 0; i < k; i++){
dp[0][2 * i + 1] = -prices[0];
}
for(int i = 1; i < prices.size(); i++){
for(int j = 0; j < k; j++){
//每一次卖出和买入的状态都和上一次卖出买入的状态有关
dp[i][2 * j + 1] = max(dp[i - 1][2 * j + 1], dp[i - 1][2 * j] - prices[i]);
dp[i][2 * (j + 1)] = max(dp[i - 1][2 * j + 1] + prices[i], dp[i - 1][2 * (j + 1)]);
}
}
return dp[prices.size() - 1][2 * k];
}
};
2.5买卖股票的最佳时机含冷冻期
状态的划分
代码实现
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
if(n == 0) return 0;
vector<vector<int>> dp(n, vector<int>(4, 0));
dp[0][0] -= prices[0];//持有股票
//0:持有股票状态（今天买入的或者是之前就买入了一直没动）
//1：保持卖出股票的状态（两天前就卖出股票，度过了冷冻期，或者是前一天卖出了股票，一直没有操作）
//2：今天卖出股票
//3：今天为冷冻状态，但是冷冻期不可持续，只有一天
for(int i = 1; i < n; i++){
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));
}
};
2.6买卖股票的最佳时机含手续费
自己的解法
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int buy = INT_MIN, sell = 0;
for(int p : prices){
buy = max(buy, sell - p - fee);
sell = max(sell, buy + p);
}
return sell;
}
};
代码随想录的实现分析方法
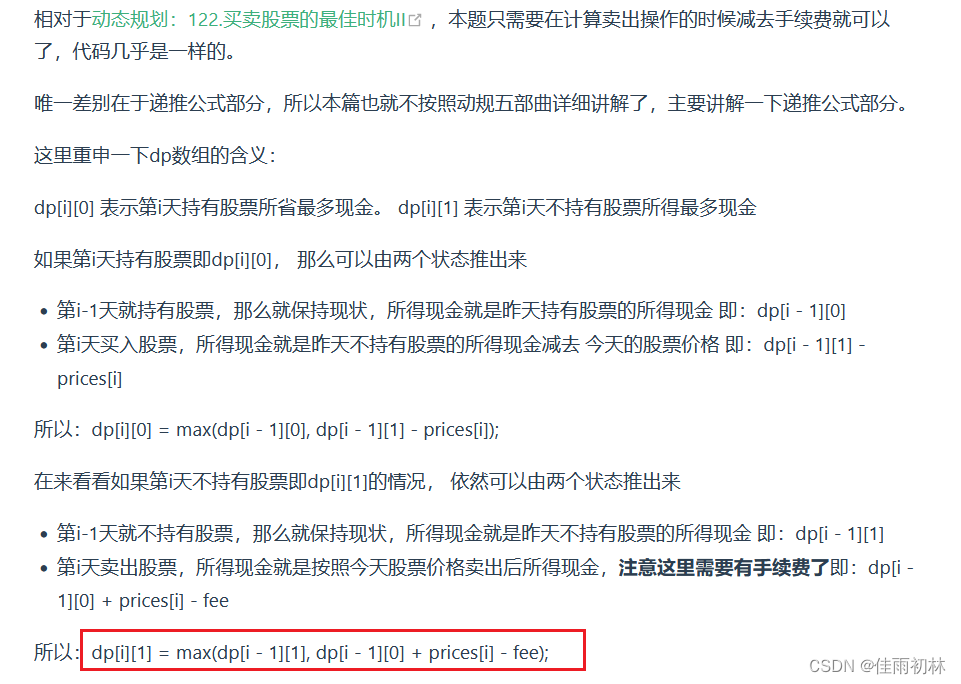
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(2, 0));
dp[0][0] -= prices[0]; // 持股票
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
}
return max(dp[n - 1][0], dp[n - 1][1]);
}
};
