预备知识
时间序列分析原理
时间序列分析之auto_arima自动调参

一、定义

ARIMA模型(Autoregressive Integrated Moving Average model)，差分整合移动平均自回归模型，又称整合移动平均自回归模型，时间序列预测分析方法之一。
$$ARIMA(p,d,q)=\{\begin{array}{ll}AR(p),& \text{p阶自回归}\\ MA(q),& \text{q阶滑动平均}\\ d,& \text{平稳时的差分阶数}\end{array}$$

ARIMA(p,d,q)中，
AR是"自回归"，p为自回归项数;
MA为"滑动平均"，q为滑动平均项数，d为使之成为平稳序列所做的差分次数(阶数)。

"差分"一词虽未出现在ARIMA的英文名称中，却是关键步骤。

1.1 AR模型（自回归）

描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测，数学模型表达式如下：
$y_t=\mu +\sum _{i=1}^p{r}_t{y}_{t-1}+{ϵ}_t$

其中是$y_t$当前值，$\mu$是常数项，p是阶数，r是自相关系数，${ϵ}_t$是误差，同时${ϵ}_t$要符合正态分布
该模型反映了在t时刻的目标值值与前t-1~p个目标值之前存在着一个线性关系

自回归模型的限制:
自回归模型是用自身的数据来进行预测
必须具有平稳性
必须具有自相关性，如果自相关系数(${\phi }_i$)小于0.5，则不宜采用
自回归只适用于预测与自身前期相关的现象

1.2 MA模型（移动平均）

移动平均模型关注的是自回归模型中的误差项的累加，数学模型表达式如下：
$y_t=\mu +{ϵ}_t+\sum _{i=1}^q{\theta }_i{ϵ}_{t-i}$

该模型反映了在t时刻的目标值值与前t-1~p个误差值之前存在着一个线性关系

移动平均法能有效地消除预测中的随机波动

1.3 ARMA模型（自回归移动平均）

ARIMA(p，d，q)模型全称为差分自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA)

该模型描述的是自回归与移动平均的结合，具体数学模型如下：
$y_t=\mu +\sum _{i=1}^p{r}_t{y}_{t-1}+{ϵ}_t+\sum _{i=1}^q{\theta }_i{ϵ}_{t-i}$

基本原理：将数据通过差分转化为平稳数据，再将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。

1.4 自相关函数ACF(autocorrelation function)

有序的随机变量序列与其自身相比较

自相关函数反映了同一序列在不同时序的取值之间的相关性

$$ACF(k)=\sum _{t=k+1}^n\frac{(Z_t-\overline{Z})(Z_{t-k}-\overline{Z})}{\sum _{t=1}^n(Z_t-\overline{Z}{)}^2}$$
取值范围为[-1,1]

自相关系数度量的是同一事件在两个不同时期之间的相关程度，形象的讲就是度量自己过
去的行为对自己现在的影响。在这里可以通过自相关系数（ACF）图的最大滞后点来大致判断q 值。

1.5 偏自相关系数（PACF）(partial autocorrelation function)

$$PACF(k)=\frac{E(Z_t-E{Z}_t)(Z_{t-k}-E{Z}_{t-k})}{\sqrt{E(Z_t-E{Z}_t{)}^2\sqrt{E(Z_{t-k}-E{Z}_{t-k}{)}^2}}}=\frac{cov[(Z_t-{\overline{Z}}_t)(Z_{t-k}-{\overline{Z}}_{t-k})]}{\sqrt{var(Z_t-{\overline{Z}}_t)\sqrt{E(Z_{t-k}-{\overline{Z}}_{t-k})}}}$$

计算某一个要素对另一个要素的影响或相关程度时，把其他要素的影响视为常数，即暂不考虑其他要素的影响，而单独研究那两个要素之间的相互关系的密切程度时，称为偏相关

对于一个平稳AR§模型，求出滞后k自相关系数p(k)时实际上得到并不是x(t)与x(t-k)之间单纯的相关关系x(t)同时还会受到中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的影响，而这k-1个随机变量又都和x(t-k)具有相关关系，所以自相关系数p(k)里实际掺杂了其他变量对x(t)与x(t-k)的影响，剔除了中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的干扰之后x(t-k)对x(t)影响的相关程度。ACF还包含了其他变量的影响而偏自相关系数
PACF是严格这两个变量之间的相关性

1.6 拖尾与截尾

拖尾：始终有非零取值，不会在k大于某个常数后就恒等于零(或在0附近随机波动)
截尾：在大于某个常数k后快速趋于0为k阶截尾

1.7 定阶

模型	ACF	PACF
AR§	衰减趋于0（几何型或振荡型）	p阶后截尾
MA (q)	q阶后截尾	衰减趋于0（几何型或振荡型）
ARMA(p,q)	q阶后衰减趋于0（几何型或振荡型）	p阶后衰减趋于0（几何型或振荡型）

截尾：落在置信区间内（95%的点都符合该规则）

因为AR（自回归）建立必须具有平稳性，所以在建立ARIMA模型也需要平稳性，使数据平稳性的方法可以讲数据进行差分处理，如一阶差分即t与t-1的差值，二阶差分为一阶差分基础上再进行一次差分，使数据平稳后的差分次数即为我们要定的参数d。

若PACFp阶段后截尾，则截尾的阶数即为模型所确定的参数p。
若ACFq阶段后截尾，则截尾的阶数即为模型所确定的参数q。

1.8 建模流程

将序列平稳（差分法确定d）

p和q阶数确定：ACF与PACF

ARIMA（p,d,q）

二、Python建模

2.1 导入相关的包

%matplotlib inline
import pandas as pd
import pandas_datareader
import datetime
import matplotlib.pylab as plt
import seaborn as sns
from matplotlib.pylab import style
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.stattools import adfuller
import numpy as np
style.use('ggplot')    
plt.rcParams['font.sans-serif'] = ['SimHei'] 
plt.rcParams['axes.unicode_minus'] = False  

import statsmodels
statsmodels.__version__
#'0.13.5'

import warnings
warnings.filterwarnings("ignore")

2.2 导入数据

我们使用一个股票的样例数据进行分析

stock = pd.read_csv('T10yr.csv', index_col=0, parse_dates=[0])
stock

Date	Open	High	Low	Close	Volume	Adj Close
2000-01-03	6.498	6.603	6.498	6.548	0	6.548
2000-01-04	6.530	6.548	6.485	6.485	0	6.485
2000-01-05	6.521	6.599	6.508	6.599	0	6.599
2000-01-06	6.558	6.585	6.540	6.549	0	6.549
2000-01-07	6.545	6.595	6.504	6.504	0	6.504
…	…	…	…	…	…	…
2016-07-25	1.584	1.584	1.554	1.571	0	1.571
2016-07-26	1.559	1.587	1.549	1.563	0	1.563
2016-07-27	1.570	1.570	1.511	1.515	0	1.515
2016-07-28	1.525	1.535	1.493	1.511	0	1.511
2016-07-29	1.525	1.530	1.458	1.458	0	1.458

4167 rows × 6 columns

#数据选取
stock_week = stock['Close'].resample('W-MON').mean()
stock_train = stock_week['2000':'2015']

Date
2000-01-03    6.54800
2000-01-10    6.53900
2000-01-17    6.66300
2000-01-24    6.73720
2000-01-31    6.67280
               ...   
2015-11-30    2.22950
2015-12-07    2.23260
2015-12-14    2.20980
2015-12-21    2.23780
2015-12-28    2.24275
Freq: W-MON, Name: Close, Length: 835, dtype: float64

2.3 数据查看

stock_train.plot(figsize=(12,6))
plt.legend(bbox_to_anchor=(1.25, 0.5))
plt.title("Stock Close")
sns.despine()

从数据走势上我们大概可以看出，是有下降的趋势的，我们用单位根来检验一下，为了方便我们写一个函数直接输出相关的数据和图

def test_stationarity(timeseries):
    
    #滑动均值和方差
    rolmean = timeseries.rolling(1).mean()
    rolstd = timeseries.rolling(1).std()

    #绘制滑动统计量
    plt.figure(figsize=(24, 8))   
    orig = plt.plot(timeseries, color='blue',label='data')
    
    plt.legend(loc='best')
    plt.title('数据展示')
    plt.show(block=False)
    
    #adf检验
    print('Results of Dickey-Fuller Test:')
    dftest = adfuller(timeseries, autolag='AIC')
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used',
                                             'Number of Observations Used'])
    for key,value in dftest[4].items():
        dfoutput['Critical Value (%s)'%key] = value
    print(dfoutput)
test_stationarity(stock_train)

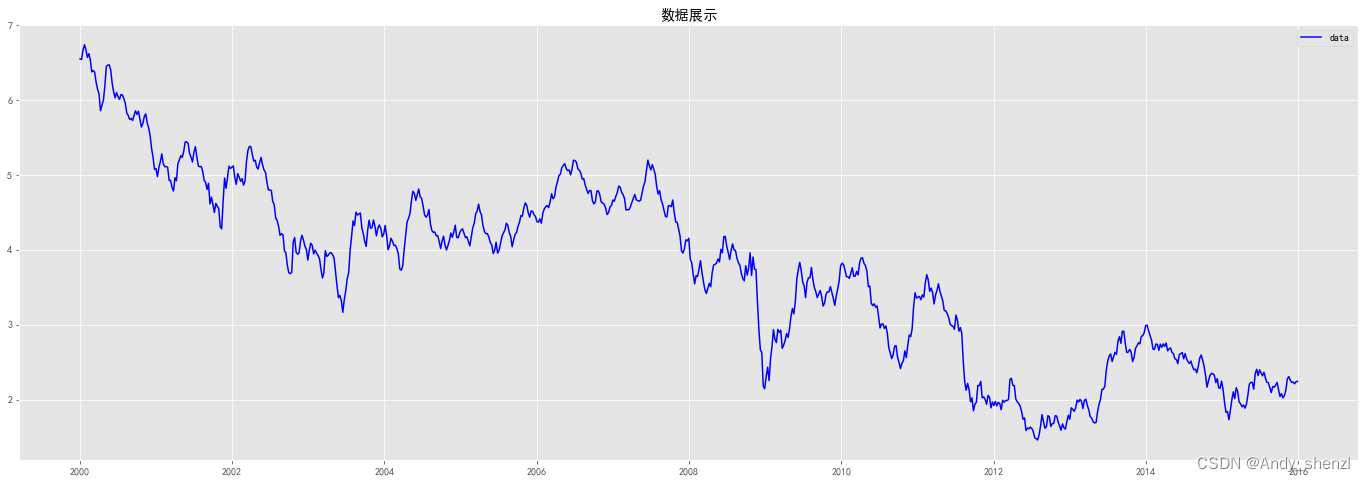
Results of Dickey-Fuller Test:
Test Statistic -2.196095
p-value 0.207666
#Lags Used 1.000000
Number of Observations Used 833.000000
Critical Value (1%) -3.438225
Critical Value (5%) -2.865016
Critical Value (10%) -2.568621
dtype: float64

P值为0.207666> 0.05，所以数据存在单位根

2.4 差分

根据上面说的，当存在单位根，即数据不平稳时需要进行差分处理。

stock_diff = stock_train.diff()
stock_diff = stock_diff.dropna()
test_stationarity(stock_diff)

直接套用上面定义的函数进行查看

Results of Dickey-Fuller Test:
Test Statistic -23.506019
p-value 0.000000
#Lags Used 0.000000
Number of Observations Used 833.000000
Critical Value (1%) -3.438225
Critical Value (5%) -2.865016
Critical Value (10%) -2.568621
dtype: float64

p-value=0.000000 ，明显是小于0.05的，所以可以拒绝存在单位根，序列已经平稳

2.5 ACF和PACF

acf = plot_acf(stock_diff, lags=20)
plt.title("ACF")
acf.show()

pacf = plot_pacf(stock_diff, lags=20)
plt.title("PACF")
pacf.show()

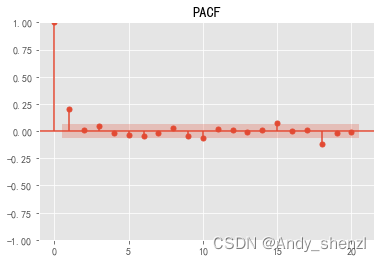
我们根据ACF和PACF的图大概可以判定p =2 ,q = 2

2.6 自动训练定阶

根据之前auto_arima介绍

from pmdarima import auto_arima

stepwise_fit = auto_arima(stock_train, 
                          start_p = 1, 
                          start_q = 1,
                          max_p = 3, 
                          max_q = 3, 
                          m = 52,
                          start_P = 0, 
                          seasonal = True,
                          d = None, 
                          D = 1, 
                          trace = True,
                          error_action ='ignore',   # we don't want to know if an order does not work
                          suppress_warnings = True,  # we don't want convergence warnings
                          stepwise = True,
                         n_jobs = -1)           # set to stepwise
  
# To print the summary
stepwise_fit.summary()

Best model: ARIMA(2,0,1)(2,1,0)[52] intercept
Total fit time: 2262.306 seconds

2.7 预测

m = 52

#Model Estimation

# Fit the model
arima2 = sm.tsa.SARIMAX(stock_train, order=(2,0,1), seasonal_order=(2,1,0,m))
model_results = arima2.fit()

#残差分析 正态分布 QQ图线性
model_results.plot_diagnostics(figsize=(15, 12));

pred = model_results.predict(start=0,end=1000)
print (pred)

plt.figure(figsize=(24, 8))   
orig = plt.plot(stock_train, color='blue',label='Original')
predict = plt.plot(pred[m+1:], color='red',label='Predict')
plt.legend(loc='best')
plt.title('Original&Predict')
plt.show(block=False)

2.8 残差分布

ERROR_RATE=(stock_train-pred[m+1:])/stock_train
plt.figure(figsize=(12,4))   
plt.scatter(ERROR_RATE.index,ERROR_RATE,color='r')
plt.grid(True)
plt.figure(figsize=(12, 4))
plt.hist(ERROR_RATE, bins=20)
plt.grid(True)
plt.show()

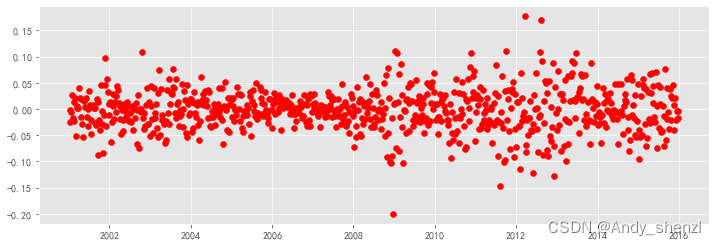
# Load specific evaluation tools
from sklearn.metrics import mean_squared_error
from statsmodels.tools.eval_measures import rmse
  
# Calculate root mean squared error
print(rmse(stock_train, pred[:m]))
  
# Calculate mean squared error
print(mean_squared_error(stock_train, pred[:m]))

1.5157632571102173
2.297538251605375