前言

本博客利用PROSAIL模型模拟出MODIS的光谱数据和LAI，然后采用支持向量回归（SVR）方法建立NDVI与LAI 的回归模型，用于LAI的反演。训练和测试数据的拟合效果还是比较好的，这表明SVR在模拟的光谱数据与LAI回归方面的可行性。

---

一、引言

叶面积指数（Leaf Area Index）为单位地表面积上植物叶片单面面积的总和。它反映了诸多因素对植被冠层结构的综合作用，是表征植被结构的重要参数，影响着植物蒸散发、光合作用、冠层截流等生物、物理过程，因此，叶面积指数也是陆地生态、水文、生物地球化学过程的重要参数。

许多卫星遥感数据可以反演LAI，常用的数据源包括MODIS、AVHHRR等高光谱数据以及Landsat卫星系列（MSS、TM、ETM+）、SPOT 和ASTER等多光谱卫星遥感数据。

目前，LAI反演方法主要有经验模型法和物理模型法。经验模型法，即回归分析方法，通常是在SVI（spectralvegetation index，如NDVI、EVI、SAVI等）与 LAI 之间，建立线性或者指数回归经验模型，是目前发展较成熟、使用最广泛的LAI 反演方法。物理模型方法通过植被冠层辐射传输模型计算LAI，其中基于几何光学模型和辐射传输模型的混合模型最具代表性。

大量研究表明植被的生物物理化学参数与光谱反射率之间的关系基本上是非线性的，拟合非线性问题的方法有多种，包括神经网络、SVM等，但神经网络的训练过程易陷入局部最优化和过学习，影响拟合和预测的精度。支持向量机SVM（supportvector machine）方法是可较好解决非线性问题的机器学习方法，它可以有效克服过学习问题并且不存在局部最解的情况，被许多学者应用到农业遥感分类与估产领域中，取得较好的效果。

我们利用PROSAIL前向模型模拟出MODIS的光谱数据,计算出归一化植被指数（Normalized DifferenceVegetation Index，NDVI），然后采用支持向量回归（SVR）方法建立NDVI与LAI 的回归模型，并用于LAI的反演。

二、PROSAIL模型及数据获取

2.1 PROSAIL模型

PROSAIL 模型由叶片光学特性模型PROSPECT 和冠层辐射传输模型SAIL耦合而成，该模型已经在生物物理化学参数反演及光谱模拟等方面广泛应用。PROSAIL模型的输入包括: 冠层理化参数、土壤参数和其他参数。本次试验所用模型为PROSAIL_5B_Fortran模型，网址为

http://teledetection.ipgp.jussieu.fr/prosail/。

（1） Prospect模型

PROSPECT 模型是基于平板模型改进的辐射传输模型，用于计算400～2500 nm 叶片半球反射率(ρ)和透过率(τ)。PROSPECT 模型包含4个参数，叶片叶绿素含量Cabμg/cm2)、叶片等效水厚度Cw (cm)、叶片干物质含率Cm (mg/cm2)，叶片内部结构参数N及棕色素含量Cbp。PROSPECT模型经过多次发展，最新版本是PROSPECT5，该版本加入了类胡萝卜素含量Car这一参数。N是描述叶片内部细胞结构的参量，与植物的种类和生长状态有关，一般情况下单子叶植物N 为1～1.5，双子叶植物N为1.5～2.5，老化叶N大于2.5。

（2）SAIL模型

SAIL模型是一维混合介质模型，将冠层看作无限延伸的连续均匀介质，并且叶片在空间随机分布。Kuusk等对SAIL模型进行了改进, 考虑了热点效应,称为SAILH（SAIL + hotspot）模型。

基于给定的结构参数和环境参数，它可以模拟任意太阳高度和观测方向的冠层反射率，主要适用于水平均匀植被或浑浊介质。SAILH模型公式如下

ρλ=SAIL(LAI,ALA,S,ρlλ,τlλ,ρsλ,skyl,Hots,θs,φs,θv,φv,VIS) (1)

式中，ρλ为冠层光谱反射率；LAI为叶面积指数；ALA为平均叶倾角(°)，ρlλ,τlλ分别为叶片反射率和透过率，由PROSPECT模型计算得到；ρsλ为土壤背景反射率，skyl为天空光散射比，Hots为热点参数；θs和φs 分别为太阳天顶角和方位角(°)，θv和φv分别为观测天顶角和方位角(°)；S=L/H为特征尺度，L 表示叶片平均尺寸和形状的水平相关长度(cm)，H为冠层高度(cm)。

因此，最终PROSAIL模型公式为

ρλ=PROSAIL(LAI,ALA,S,Cab,Cw,Cm,Cbp,Car,N,ρsλ,skyl,Hots,θs,φs,θv,φv,VIS) (2)

2.2参数选取

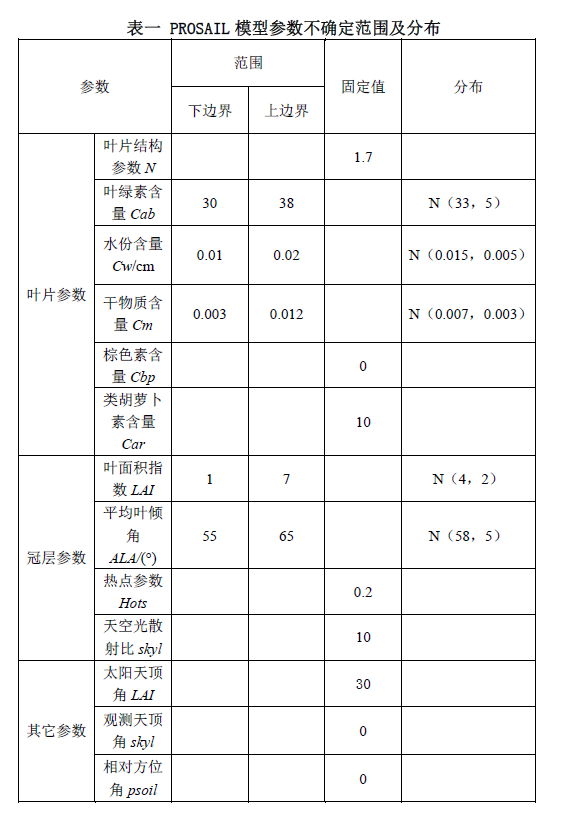
本次试验需要模拟LAI及基于MODIS响应函数的光谱变化情况，模拟数据通过PROSAIL模型获取。PROSAIL模型的输入参数及其不确定范围根据一些先观测值及文献确定。这些参数的不确定范围及分布如表一所示，其中N（33,5）表示均值为33，方差为5的正态分布。

2.3数据模拟及处理

由于本次试验要根据NDVI来拟合LAI的变化情况，而MODIS对应的红光及近红外波段分别为band1和band2，那么根据表一中的参数设定，调用PROSAIL获取LAI及MODIS band1和band2对应的光谱积分数据。试验拟获取10000个样本，每个样本的输入参数均由表一随机分布函数随机产生。为使模拟数据能够更好地逼近真实情况，积分后的光谱数据加有2%的高斯白噪声。图一以叶绿素含量Cab的生成为例说明随机输入参数的产生情况，其中，NormalRandom为正态随机分布函数。

2.4NDVI计算

（1）公式

NDVI= (NIR-R)/(NIR+R) (3)

其中NIR和R分别表示近红外波段和红光波段对应数值。

（2）原理

植物叶片组织对蓝光(470nm)和红光(650nm)有强烈吸收，而对绿光和红外光强烈反射。叶片中心的海绵组织和叶片背面组织对近红外辐射(NIR，700-1000nm)反射较强。从红光(Red)到红外光，裸地反射率较高但增幅很小。植被覆盖越高，红光反射越小，近红外光反射越大。红光吸收很快达到饱和，而近红外光反射随着植被增加而增加。所以，任何强化Red 和NIR差别的数学变换都可以作为植被指数，来描述植被状况。MODIS传感器band1光谱范围为620～670nm，为红光波段，band2光谱范围为841～876nm，为近红外波段，因此可以用band1和band2来计算NDVI。

最终模拟出的10000个样本的LAI和NDVI序列如图1和图2所示。图1指LAI和NDVI两个序列的分布情况，图三是LAI和对应NDVI的散点分布图。

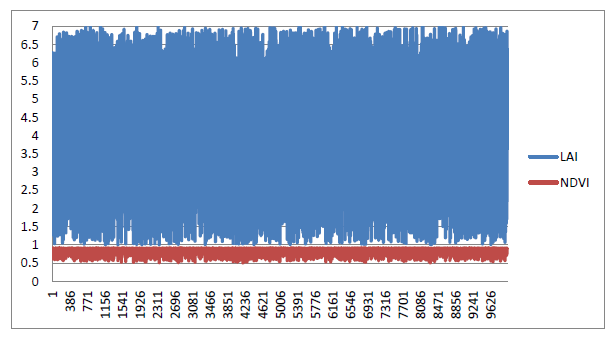
图1 LAI 和 NDVI 样本折线图

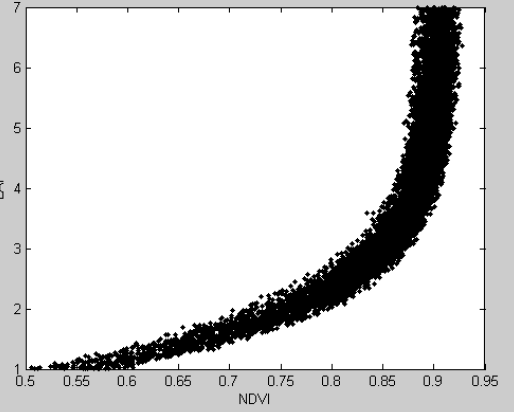
图2 LAI 和 对应 NDVI 样本 散点图

三、支持向量回归(SVR)及LAI反演

3.1SVR简介

支持向量机是Vapnik及其研究小组于20世纪90年代初期在现代统计学习理论的基础上提出来的一类新型机器学习方法。

支持向量机起初是解决两类样本的分类问题，其核心思想是找到一个最优分类超平面

ω*x+b=0 (4)

使两类样本的分类间隔最大化。支持向量回归与支持向量分类相似，不同之处在于，回归所求超平面是使所有样本点到超平面的距离为最小。

对于线性同归问题，实质上是寻求一个最优超平面，使得在给定精度ε(ε≥O)条件下可以无误差的拟合y，，即所有样本点到最优超平面的距离都不大于ε；考虑到允许误差的情况，可引入松弛变量ξ和ξ*(ξ、ξ*≥o)以及惩罚参数C(C>O)，其寻优问题转化为相应的二次规划问题如下

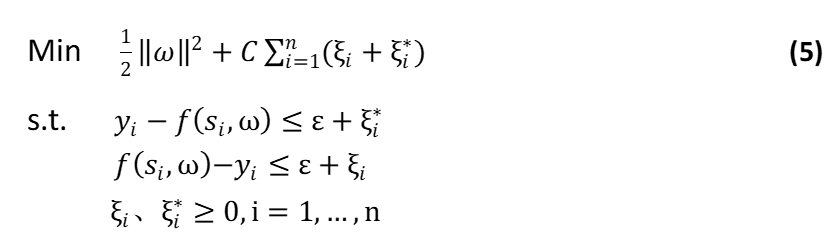
对于非线性回归问题，可通过核函数变换将样本映射到一个高维特征空间中用线性回归来解决。通常，特征空间维数很高甚至具有无穷维数，致使空间变换后计算量巨增而面临维数灾难等问题。但是，支持向量机中待解的对偶问题只包含一个变换后特征空间的内积运算，而这种运算能在原空间中通过核函数来实现。根据Mercer定理可构造系列核函数，常见如线性核、多项式核、多项式核、高斯径向基核(RBF)和sigmoid核等。

3.2最优参数选取

通常，支持向量回归需要先对样本进行分割，然后训练、选取最优参数。由于生成的10000个样本为随机产生，所以样本的分割过程比较简单，采取4:1的分割比例，前8000个样本做训练，后2000个样本做测试。样本中NDVI做自变量，LAI做因变量。

本次试验采用libsvm3.14，下载网址为

http://www.csie.ntu.edu.tw/~cjlin/libsvm/。试验调试的是matlab版本，采用ε-SVR，核函数是高斯径向基函数RBF，函数如公式(6)所示。

Kxi,x=exp⁡(-γ*x-xi2) (6)

其中，γ是宽度参数。

（1）惩罚系数C

Cherkassky等认为，一个好的惩罚系数C可以代表训练样本的变化范围。但是C对极值较为敏感，因此可以采用公式(7)的形式表示。

C=max⁡(y+3σy,y-3σy) (7)

其中，y，σy分别指训练样本的均值和方差。

对于本次试验的训练样本来说，C=8.396.

（2）不敏感性损失ε和宽度γ

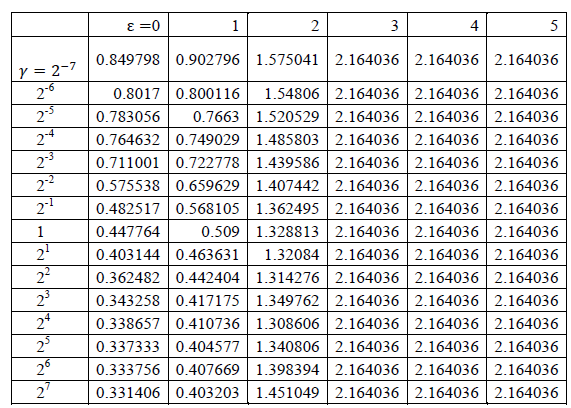
这两个参数的确定通过5折的交叉互检验确定。首先，给定γ 2^[-7:7]15个取值、ε [0:5]共6个取值。同样，由于训练样本的随机性，就按顺序分割训练样本为五个样本。每折检验中，其中一个样本做验证，剩下四个样本做训练，对应的15*6组参数各进行一次建模，统计误差平方和并进行累加。五折交叉互检验结束后，累加误差平方和最小的参数组合即为最优组合。误差平方和矩阵如表二所示。其中对应最小误差平方和为0.331406，对应ε 和γ 分别为128和0。

表二 五折交叉互检验后不同参数组合的最小误差平方和

3.3 LAI反演

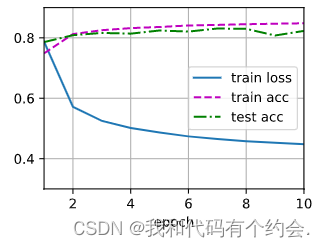
3.2部分确定了SVR模型及核函数，然后选取了SVR的三个最优参数，这样就可以建立回归模型。模型建立好之后可以对剩下的2000个样本做测试。拟合结果的统计指标为RMSE。训练和测试数据的RMSE和回归系数如表三所示。训练数据的RMSE为0.331171，测试数据的RMSE为0.355843，达到较好的拟合效果。

对训练、测试、模型预测数据做散点图，如图四所示，模型很好地拟合了样本的变化情况。

表三 训练、测试数据的RMSE和回归系数

图3 训练、测试和模型模拟数据散点图

---

总结

本文尝试利用PROSAIL模型模拟出MODIS的光谱数据和LAI，然后采用支持向量回归（SVR）方法建立NDVI与LAI 的回归模型，用于LAI的反演。从结果来看，回归的效果还是不错的，训练和测试数据的RMSE分别为0.331171和0.355843，这表明SVR在模拟的光谱数据与LAI回归方面具备可行性。但是，本试验同时也存在一些问题，

(1) libsvm3.14 matlab版本没有生成scaleSVM函数，即回归之前数据没有归一化，这或许会对拟合效果有影响；

(2) 本次试验中所有的数据均为模拟数据，没有使用遥感数据和实测数据建模，后续的研究中会尝试模拟和非模拟数据相结合；

(3) 本次试验直接选取ε-SVR和RBF，虽然有最优参数筛选过程，但同时也可能存在其他的SVR（如LS-SVR等）和其他的核函数（如sigmoid核函数等）组合反演效果较好的情况；

(4) Vohland等认为，在LAI较大时，光谱数据（反射率或NDVI）的敏感性变低，这在图2、3中可以看出，当LAI>4时，NDVI出现饱和现象，这也有可能影响回归，可以对LAI分段拟合。具体工作会在后续研究中体现。