问题描述

n 个小朋友排成一排，从左到右依次编号为 1∼n。

第 i 个小朋友的身高为 hi。

虽然队伍已经排好，但是小朋友们对此并不完全满意。

对于一个小朋友来说，如果存在其他小朋友身高比他更矮，却站在他右侧的情况，该小朋友就会感到不满。

每个小朋友的不满程度都可以量化计算，具体来说，对于第 i 个小朋友：

如果存在比他更矮且在他右侧的小朋友，那么他的不满值等于其中最靠右的那个小朋友与他之间的小朋友数量。
如果不存在比他更矮且在他右侧的小朋友，那么他的不满值为 −1。
请你计算并输出每个小朋友的不满值。

注意，第 1 个小朋友和第 2 个小朋友之间的小朋友数量为 0，第 1 个小朋友和第 4 个小朋友之间的小朋友数量为 2。

输入格式
第一行包含整数 n。

第二行包含 n 个整数 h1,h2,…,hn。

输出格式
共一行，输出 n 个整数，第 i 个整数为第 i 个小朋友的不满值。

数据范围
前 5 个测试点满足 2≤n≤5。
所有测试点满足 2≤n≤10⁵，1≤hi≤10⁹。

输入样例1：

6
10 8 5 3 50 45

输出样例1：

2 1 0 -1 0 -1

输入样例2：

7
10 4 6 3 2 8 15

输出样例2：

4 2 1 0 -1 -1 -1 

输入样例3：

5
10 3 1 10 11

输出样例3：

1 0 -1 -1 -1 

分析

这道题的数据量是10的5次方，因此我们的算法最终的时间复杂度要控制在nlogn或者n。

1、两层循环（超时）

#include<iostream>
#include<cstring>
using namespace std;
const int N=2e5+10;
int n;
int a[N];
int h[N];
int main()
{
    memset(h,-1,sizeof h);
    cin>>n;
    for(int i=0;i<n;i++)
    {
        scanf("%d",a+i);
    }
    for(int i=0;i<n;i++)
    {
        int t=0;
        for(int j=i+1;j<n;j++)
        {
            if(a[j]<a[i])t=j;
        }
        if(t>0)
        h[i]+=t-i;
    }
    for(int i=0;i<n;i++)
    {
        cout<<h[i]<<" ";
    }
    return 0;
}

2、单调栈+二分（nlogn）

我们发现这道题是让我们找小于当前数的最右侧的一个，那么我们倒着遍历这个数组。
我们看下面这个图：

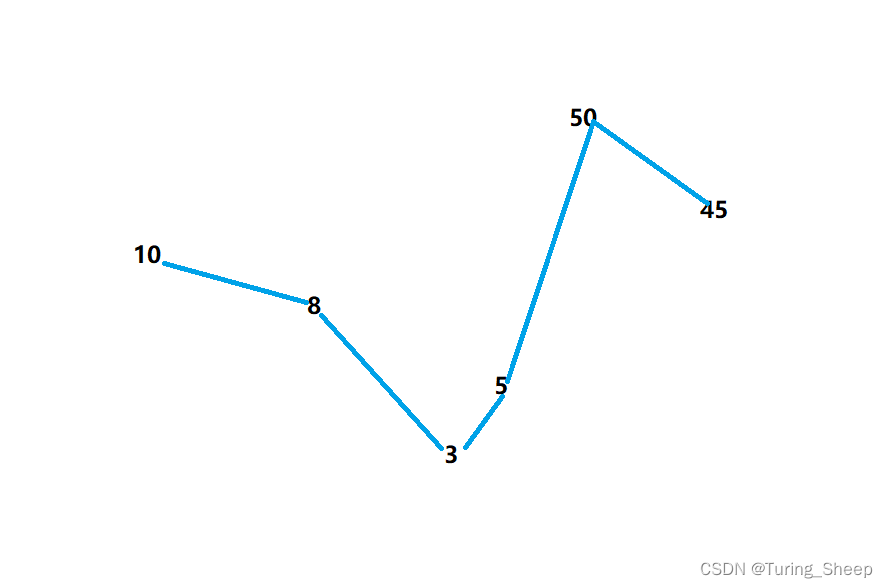
我们按照数字本身的大小将其画成上面的折线图，我们从右往左看，假设存在一个数大于50，那么他肯定大于45，所以而45又在50的右侧，所以这个50必定不是答案。按照这个思路，我们在从右往左遍历的过程中，我们只需要让小于栈顶元素的数入栈，因为大于栈顶的元素必定不是答案，所以没必要入栈。即下图：

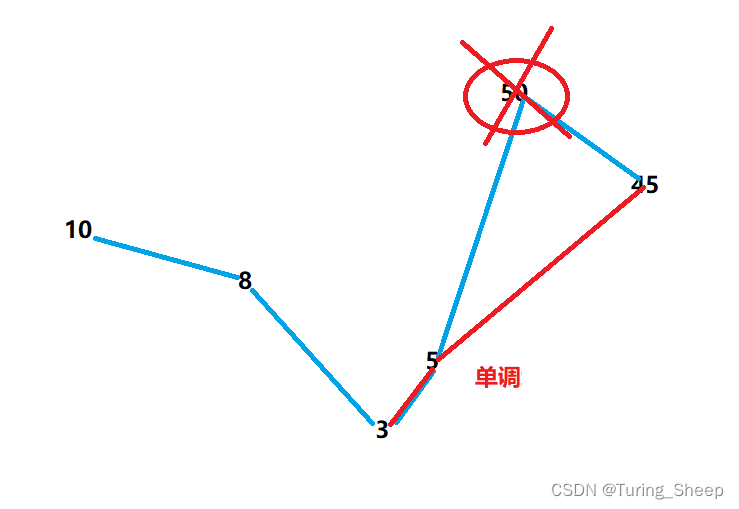
当我们想找比8小的最右侧元素的时候，我们只需要去栈中找。我们发现，栈中的元素是单调的。因此，我们可以采用二分法去找。

#include<iostream>
#include<algorithm>
#include<cstring>
const int N=1e5+10;
int a[N],stk[N],top;
int ans[N];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)scanf("%d",a+i);
    for(int i=n-1;i>=0;i--)
    {
        if(!top||a[i]<=a[stk[top]])
        ans[i]=-1;
        else
        {
            int l=1,r=top;
            while(l<r)
            {
                int mid=l+r>>1;
                if(a[stk[mid]]<a[i])r=mid;
                else l=mid+1;
            }
            ans[i]=stk[r]-i-1;
        }
        if(!top||a[i]<a[stk[top]])stk[++top]=i;
    }
    for(int i=0;i<n;i++)
    {
        printf("%d ",ans[i]);
    }
    return 0;
}