本题力扣上没有,是刷的卡码网第46题感兴趣的小伙伴可以去刷一下,是ACM模式。本篇讲解二维dp数组来解决01背包问题,下篇博客将用一维dp数组来解决01背包问题。
题目:
46. 携带研究材料
时间限制:5.000S 空间限制:128MB
题目描述:
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。他需要带一些研究材料,但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等,它们各自占据不同的空间,并且具有不同的价值。
小明的行李空间为 N,问小明应该如何抉择,才能携带最大价值的研究材料,每种研究材料只能选择一次,并且只有选与不选两种选择,不能进行切割。
输入描述:
第一行包含两个正整数,第一个整数 M 代表研究材料的种类,第二个正整数 N,代表小明的行李空间。
第二行包含 M 个正整数,代表每种研究材料的所占空间。
第三行包含 M 个正整数,代表每种研究材料的价值。
输出描述:
输出一个整数,代表小明能够携带的研究材料的最大价值。
输入示例:
6 1
2 2 3 1 5 2
2 3 1 5 4 3
输出示例:
5
提示信息:
小明能够携带 6 种研究材料,但是行李空间只有 1,而占用空间为 1 的研究材料价值为 5,所以最终答案输出 5。
数据范围:
1 <= N <= 1000
1 <= M <= 1000
研究材料占用空间和价值都小于等于 1000
思路:
01 背包:
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
二维dp数组01背包:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
依然动规五部曲分析。
- 确定dp数组以及下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
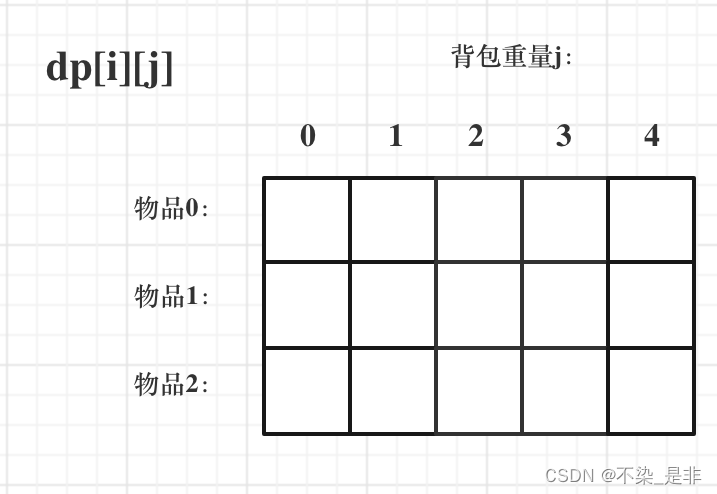
要时刻记着这个dp数组的含义,下面的一些步骤都围绕这dp数组的含义进行的,如果哪里看懵了,就来回顾一下i代表什么,j又代表什么。
- 确定递推公式
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有两个方向推出来dp[i][j],
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
- dp数组如何初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
如图:

在看其他情况。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
代码初始化如下:
# 创建二维数组dp,用于保存状态转移的结果
dp = [[0] * (bag_weight + 1) for _ in range(bag_nums)]
# for i in range(bag_nums): 此处已把所有dp数组初始为0了 故此步可省略
# dp[i][0] = 0
# 初始化第一个背包的状态
for j in range(weight[0], bag_weight + 1):
dp[0][j] = value[0]
此时dp数组初始化情况如图所示:
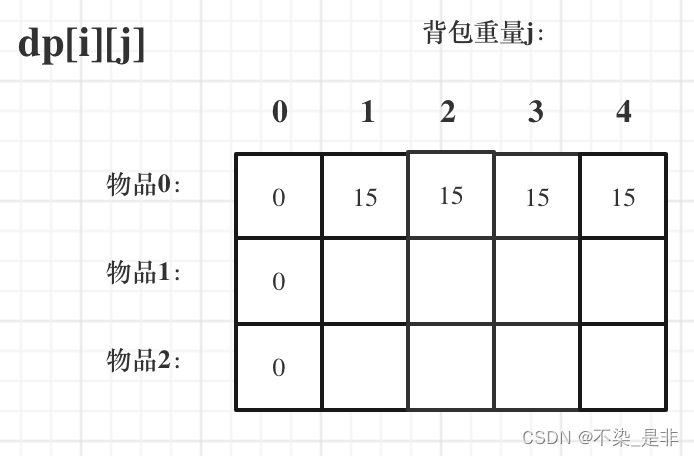
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
其实从递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由左上方数值推导出来了,那么 其他下标初始为什么数值都可以,因为都会被覆盖。
初始-1,初始-2,初始100,都可以!
但只不过一开始就统一把dp数组统一初始为0,更方便一些。
最后初始化代码如下:
def result():
# 读取输入的数据
N = [int(x) for x in input().split()] # 读取背包数量和背包总重量
weight = [int(x) for x in input().split()] # 读取每个物品的重量
value = [int(x) for x in input().split()] # 读取每个物品的价值
bag_nums = N[0] # 背包数量
bag_weight = N[1] # 背包总重量
# 创建二维数组dp,用于保存状态转移的结果
dp = [[0] * (bag_weight + 1) for _ in range(bag_nums)]
# 初始化第一个背包的状态
for j in range(weight[0], bag_weight + 1):
dp[0][j] = value[0]
到了这里应该有很多人还是不太明白代码为什么这么写,为什么j要从weight[0]开始遍历到bag_weight 结束(这里的代码是直接看着题目描述的输出和输入案例来AC的),我刚开始也不太理解,后来发现还是自己没审好dp数组的初始化步骤和过程,dp数组首先对第一列开始全部初始化为0(我在定义dp数组的时候就已经全部初始化为0了,所以此步骤可以省略)
之后把第一行初始化,这里初始化并不需要排序啊什么的,就取weight数组的第一个元素,看它是否满足小于背包(bag_weight)的重量,如果小于则把该weight数组第一个元素对应重量下的value(价值)赋给dp[0][j],从dp[0][j]到dp[0][bag_weight]全部都赋值为value[0]
- 确定遍历顺序
在上述图片中可以看出,有两个遍历的维度(两层for循环):物品与背包重量
那么问题来了,先遍历 物品还是先遍历背包重量呢?
其实都可以!! 但是先遍历物品更好理解。
- 举例推导dp数组
来看一下对应的dp数组的数值,如图:
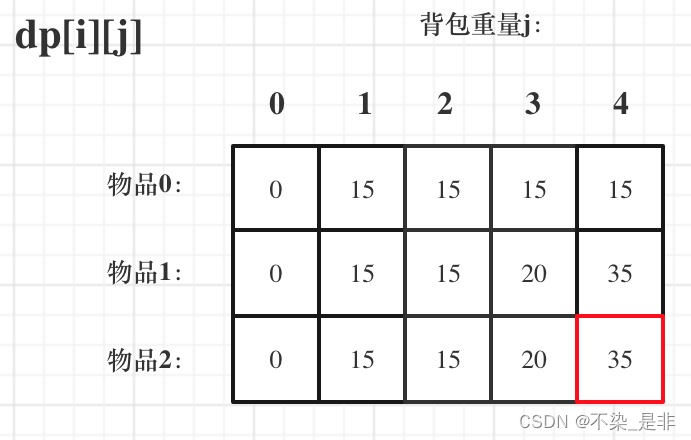
这里其实就是确认最后的返回值是什么,因为dp数组的含义是最大的价值(不管重量如何变化,取的都是最大的价值总和),所以应该返回dp数组的最后一个元素
return dp[bag_nums - 1][bag_weight] # 返回最后一个背包的最大价值
代码及详细注释:
def result():
# 读取输入的数据
N = [int(x) for x in input().split()] # 读取背包数量和背包总重量
weight = [int(x) for x in input().split()] # 读取每个物品的重量
value = [int(x) for x in input().split()] # 读取每个物品的价值
bag_nums = N[0] # 背包数量
bag_weight = N[1] # 背包总重量
# 创建二维数组dp,用于保存状态转移的结果
dp = [[0] * (bag_weight + 1) for _ in range(bag_nums)]
# 初始化第一个背包的状态
for j in range(weight[0], bag_weight + 1):
dp[0][j] = value[0]
# 状态转移,计算每个背包的最大价值
for i in range(1, bag_nums):
for j in range(1, bag_weight + 1):
if j < weight[i]:
dp[i][j] = dp[i - 1][j] # 当前背包的重量大于背包总重量,不放入当前物品
else:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]) # 放入当前物品或者不放入当前物品,取最大值
return dp[bag_nums - 1][bag_weight] # 返回最后一个背包的最大价值
if __name__ == '__main__':
print(result()) # 输出结果