目录

题目描述

输入描述

输出描述

用例

题目解析

算法源码

---

题目描述

给定一组闭区间，其中部分区间存在交集。

任意两个给定区间的交集，称为公共区间(如:[1,2],[2,3]的公共区间为[2,2]，[3,5],[3,6]的公共区间为[3,5])。

公共区间之间若存在交集，则需要合并(如:[1,3],[3,5]区间存在交集[3,3]，需合并为[1,5])。

按升序排列输出合并后的区间列表。

输入描述

一组区间列表，

区间数为 N: 0<=N<=1000;

区间元素为 X: -10000<=X<=10000。

输出描述

升序排列的合并区间列表

备注:

1、区间元素均为数字，不考虑字母、符号等异常输入。

2、单个区间认定为无公共区间。

用例

输入	4 0 3 1 3 3 5 3 6
输出	1 5
说明	无

输入	4 0 3 1 4 4 7 5 8
输出	1 3 4 4  5 7
说明	无

输入	2 1 2 3 4
输出	None
说明	无

题目解析

首先，输入的多组区间，我们需要求解任意两组之间的交集，

求两个区间交集的方式：[两个区间中较大的起点，两个区间中较小的终点] 

 

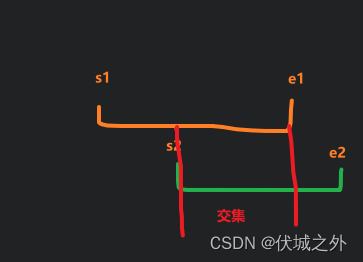
求出所有交集后，我们合并交集时，是可以先对交集进行排序的，排序后更好合并，关于区间的合并的逻辑，请看华为机试 - 路灯照明问题_伏城之外的博客-CSDN博客

算法源码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

const lines = [];
let n;
rl.on("line", (line) => {
  lines.push(line);

  if (lines.length === 1) {
    n = parseInt(lines[0]);
  }

  if (n && lines.length === n + 1) {
    lines.shift();
    const intervals = lines.map((line) => line.split(" ").map(Number));
    union(intervals);

    lines.length = 0;
  }
});

function union(intervals) {
  // intersections用于保存交集
  const intersections = [];

  // 任意两区间的交集
  for (let i = 0; i < intervals.length; i++) {
    for (let j = i + 1; j < intervals.length; j++) {
      const [s1, e1] = intervals[i];
      const [s2, e2] = intervals[j];
      const left = Math.max(s1, s2);
      const right = Math.min(e1, e2);
      if (left <= right) {
        intersections.push([left, right]);
      }
    }
  }

  if (!intersections.length) return console.log("None");

  // 合并交集
  const mergeRes = intersections
    .sort((a, b) => a[0] - b[0])
    .reduce((pre, cur) => {
      const [s1, e1] = pre;
      const [s2, e2] = cur;

      if (e1 >= s2) {
        pre = [s1, Math.max(e1, e2)];
      } else {
        console.log(pre.join(" "));
        pre = cur;
      }
      return pre;
    });

  console.log(mergeRes.join(" "));
}