参考：https://zhuanlan.zhihu.com/p/166199924，https://www.runoob.com/w3cnote/ten-sorting-algorithm.html
**稳定性：**是表示相同值的数据在排序好的结果中的位置前后关系依然不会变，例如[3,1,3],排序后的最后一个3位置不变，只是第一个3和第二个1换了位置
**时间复杂度：**对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律
排序方式：In-place,和Out-place表示是否需要额外内存空间

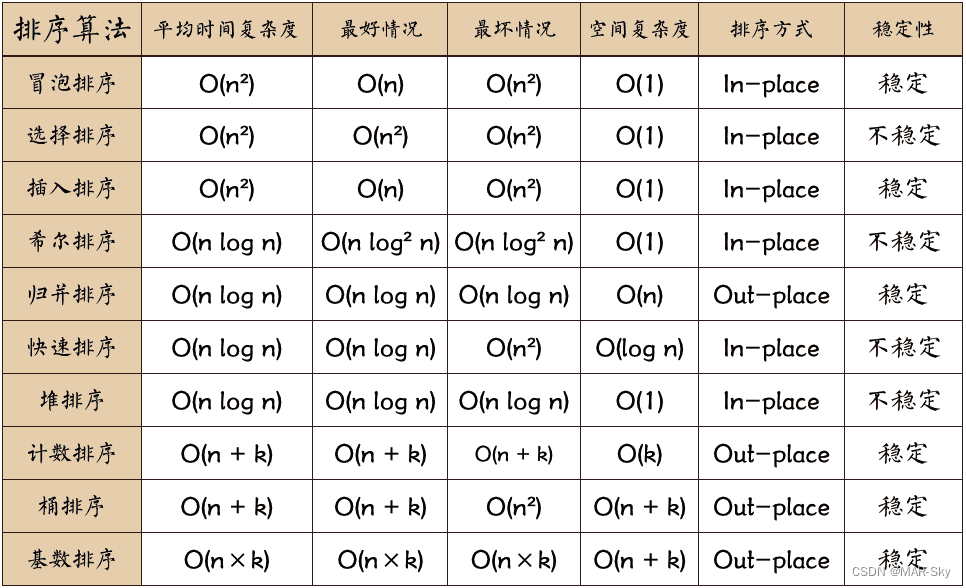
各种排序方法

冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序、计数排序、桶排序、基数排序

各种排序动图演示

参考:

各种排序个人简介

冒泡排序（bubble sort）

相邻的数据比较得到较大值，然后把较大值放在右侧，并以这个较大值为基准，再向右比较，最终的右边数据是整个数据最大。因此，相等的数据不会改变位置相对关系，是稳定排序。

选择排序(selection sort)

将空间分为两部分：无序空间；无序空间。将无序空间中的最小（大）比较选出来，然后将这个数据放入有序的空间。比较过程中当遇到满足条件的数据，直接将索引交换，而不是像冒泡排序每比较一次就要换位置或修改最大标记的指向。例如，5 8 5 2 9，比较过程中第一个5的索引和2的索引直接交换，导致下次比较时，原来右边的位置却先被放入有序空间中，因此这是不稳定的排序

插入排序(insertion sort)

假设第一个数字有序，将后边的数字一个一个的插入前面有序的地方。比较的方式是将无序的一个数和前面有序的数据从右向左比较，当比较的值比无序的值大时才交换位置。因此同样大小的数据不会交换位置，所以也是稳定排序。

希尔排序（Shell Sort）

将数据每隔一个增量k做为一组进行插入排序，例如[1,2,3,4,5,6,7,8],把增量为3作为一组进行排序，分成[1,4,7]和[2,5,8]和[3,6]三个个组，对每个组进行进行一趟插入排序（注意实在原有的位置上比较两组数据和修改索引位置）。第二次减少增量值，重复操作，知道增量为1会对所有的数据进行插入排序，但前面的操作几乎把数据拍好，很少需要调整。但和插入不同相同，这是不稳定的排序，因为分组时可能出现某一个组较大，把和另一组相同的数据放入更前面。

归并排序（merge sort）

将数据全部分散开，对于二路归并，将每两个进行比较生成一个只包含两个数据的有序数组；然后将只包含两个有序数据的数据归并成4个有序的数组；依次处理到最后把整个数据都归并成有序的。这是一个稳定的排序。

快速排序（quick sort）

首先，规定一个基准，然后把数据分为全部大于该基准和全部小于该基准的两部分，利用同样的思想对这两个子部分进行排列有序，合并后就有序

堆排序（Heap Sort）

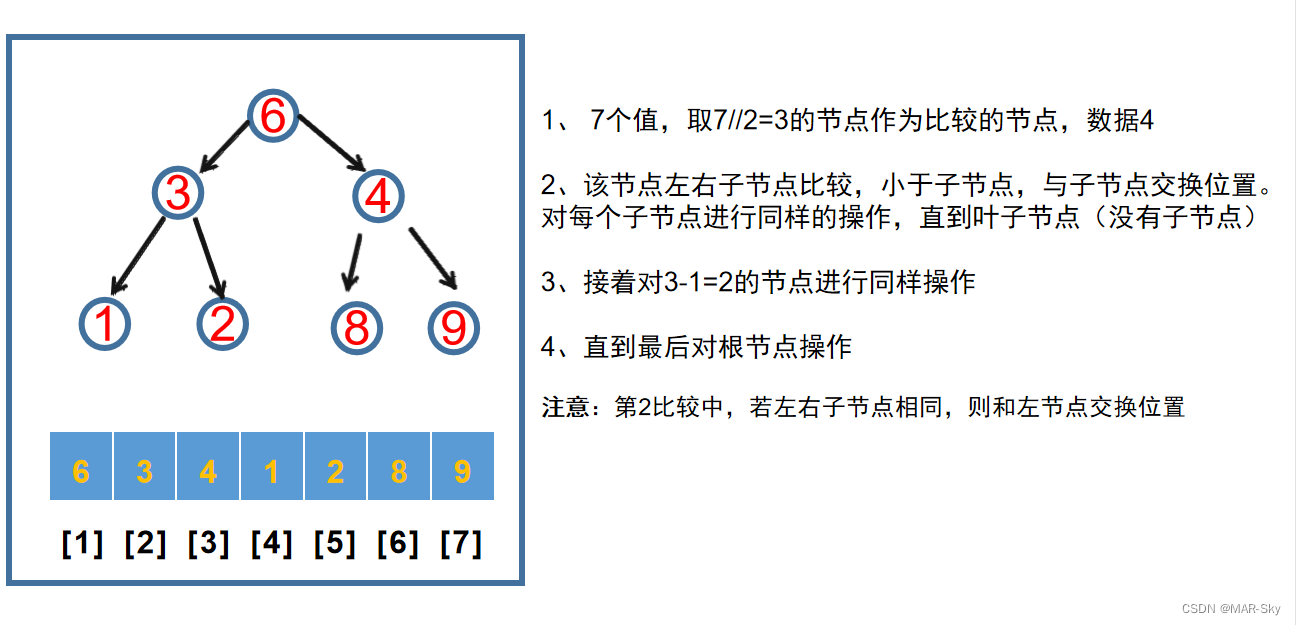
堆：一种数据结构，最大堆是每一个节点的键值不小于其孩子节点。例如[9, 6, 8, 3, 1, 4, 2]

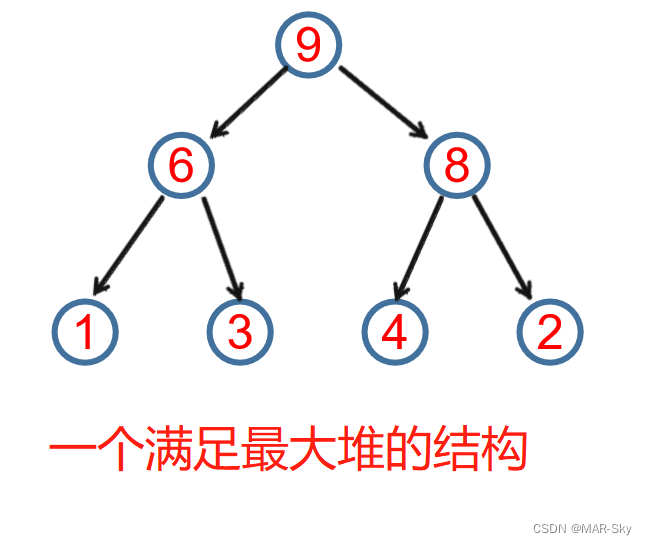
从上面的堆来说，根节点一定是最大的值。把它和最右下的节点交换，然后把剩下的堆调整到一个新的堆。接着取出调整后的根节点和最后一个子节点交换位置，依次得到一个有序的堆。堆调整过程，先找到要调整比较的节点，取的是总节点数的1/2取整的节点索引。然后和左右子节点最大的比较，若父节点小，则交换位置，若两个子节点的大小相同，这交换的是左节点的索引。但对于已经调整好的堆只是交换了开头和结尾后的数据，直接将根节点作为比较节点就行。因为，除了被交换的两个节点，其他节点已经满足最大堆的规律。这种明显是不稳定的排序

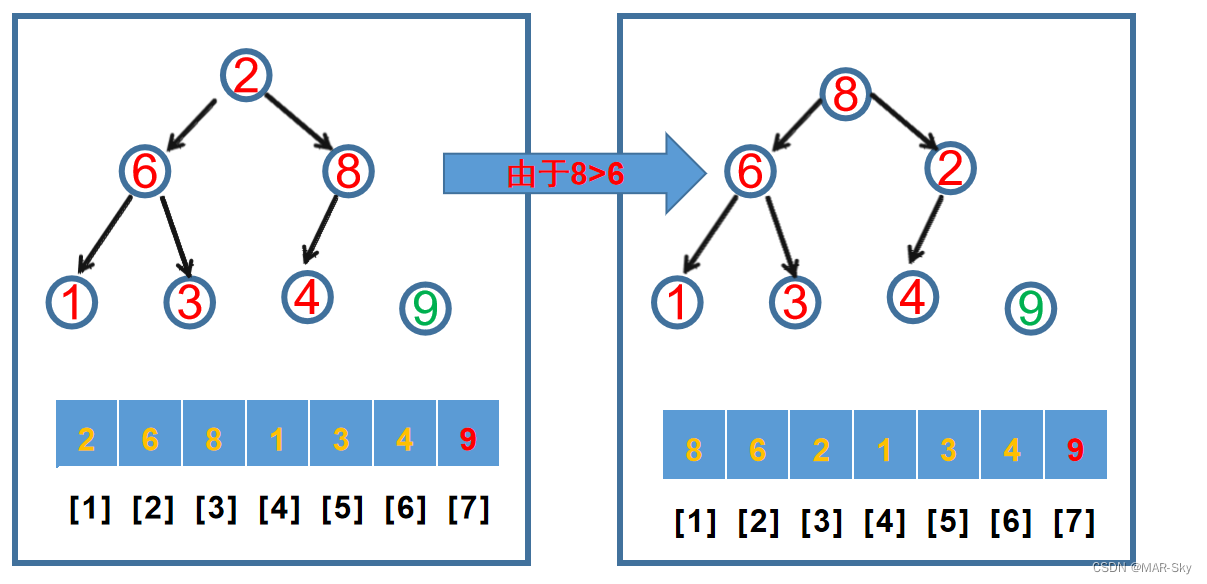
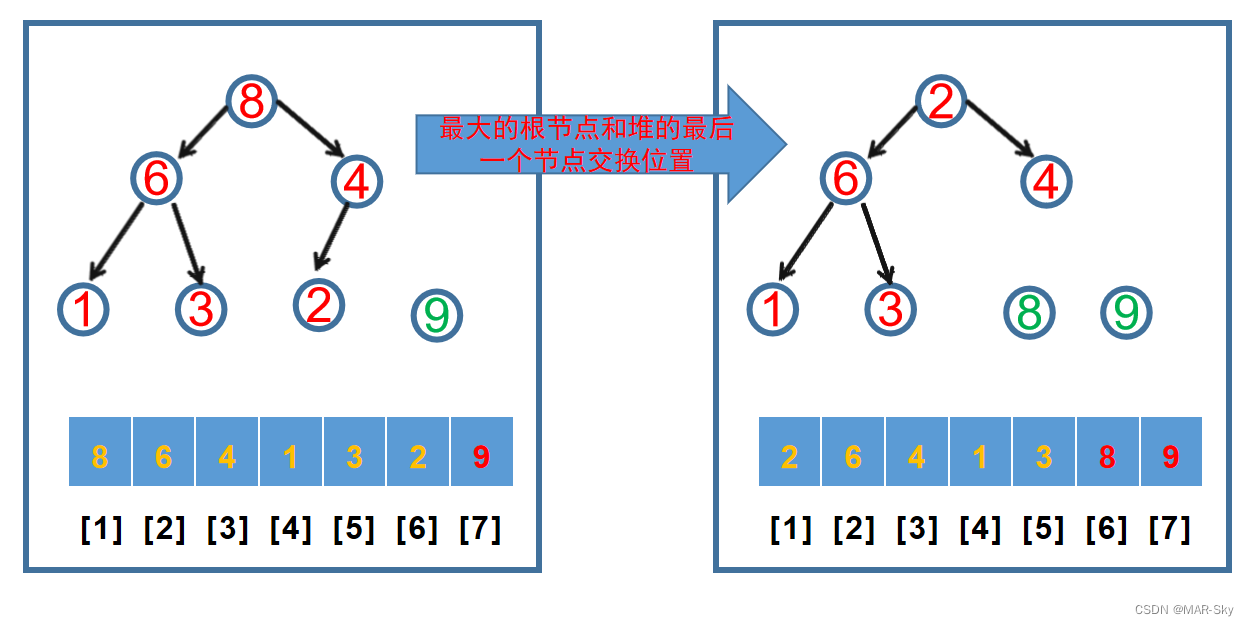
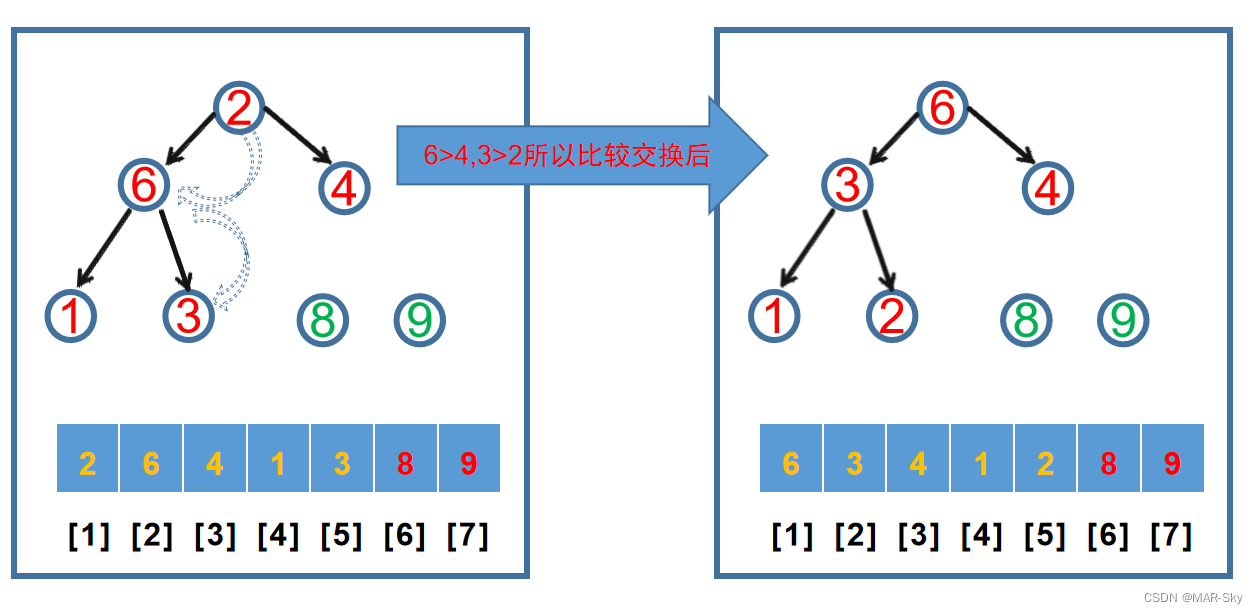
计数排序（bubble sort）

这种方式不是基于比较的，是根据记录每一个数据的数量，然后将记录的数量输出。
先找到所有要排列数据的最大最小值。统计出每个数据的出现次数。然后将统计出的次数，根据数据的大小顺序，进行反向输出，每输出一个就把记录的次数减去1。对于不密集的数据建立字典会有很大的浪费。这种排序可以说和原来相同大小数据的位置没什么关系了，根本说不上稳定还是不稳定吧，但看资料中写的是稳定。

桶排序（Bucket Sort）

设置多个”桶“可以存放某段的数据，例如，设置0桶可存放0到9的数据，1桶存放10到19的数据等。将这些分开的非空的数据桶进行排序，最后只要把这些桶拼接在一起就行。这种排序是稳定的

基数排序（Radix Sort）

可以理解为从低位开始只看某一位大小，将数据放入0到9的桶内。第一次，根据个位上数字的大小，可以将数据分成10组，然后将每一个数组的数据根据先放入先拿出的规则重新列出来；然后看10位上的数字大小，放入0到9的桶内。假设最大就是两位数字，这时同一个桶里的小数一定被先放进去，因为十位相同但个位大的数据在后面。使用参考连接中的gif图更清晰，这是稳定的排序