整型提升是什么?
- 整型提升的规则
- 整型提升的存在
整型提升:
在计算机中,一个数据的类型如果是char 类型,以整型的形式打印该char类型的值时,会自动转换成整型,叫做整型提升。
整型提升的规则:
整型提升是按照变量的数据类型的符号位来提升
举例说明整型提升的存在:
int main()
{
char a = -1;
signed char b = -1;
unsigned char c = -1;
printf("a=%d,b=%d,c=%d", a, b, c);
}
输出的结果是什么?
来一个个分析:
对于char a = -1;
先写出-1的原码反码和补码
10000000000000000000000000000001 - 原码
1111111111111111111111111111111111110 - 反码
1111111111111111111111111111111111111 - 补码
在内存中是以补码来运算的
把-1的补码放入a中,由于a是char类型,不足以存放-1,所以会发生截断,a是一个字节的大小,存放8个比特位,所以a中存放的是 11111111
打印的时候,是以%d的形式打印的,%d打印的是有符号的正数。故a会发生整型提升,提升到一个整型的大小。
根据整型提升的规则:
整型提升是按照变量的数据类型的符号位来提升
所以a提升的时候,是按照符号位的数值来提升的,a的符号位是1,提升的时候补全1。
所以a提升后的补码为11111111111111111111111111111111。提升后,打印结果出来,**而打印的时候是以原码来打印的。**故a需要转换成原码打印出来,%d认为,a提升后的第一位是符号位,所以变成原码时,符号位不变,其它位按位取反再+1,此时a提升后的原码为:10000000000000000000000000000001,转换成十进制的结果是 -1 .
对于b来说,signed char b = -1,与上面同理,-1的补码是 1111111111111111111111111111111111111 ,存入b中,b是signed char类型,不足以存放32比特位,只能存放8比特位,故b中存放的是 11111111 , 以%d的形式打印出来,同样进行整型提升,%d认为第一位是符号位,故b打印出来也是 -1。
而对于c,-1的补码表示出来,1111111111111111111111111111111111111 ,存入c中,由于c 是unsigned char 类型,故会发生截断,存入c的补码是 11111111,以%d的形式打印出来,由于c是无符号char类型,故第一位不是符号位,对于无符号类型来说,整型提升补0,故c整型提升后的结果为:00000000000000000000000011111111 - c整型提升后的补码。由于%d认为,第一位是符号位,符号位是0,故c整型提升后的补码是一个正数,正数的原码反码补码相同,故c整型提升后的补码也是原码。打印出来的结果是255。
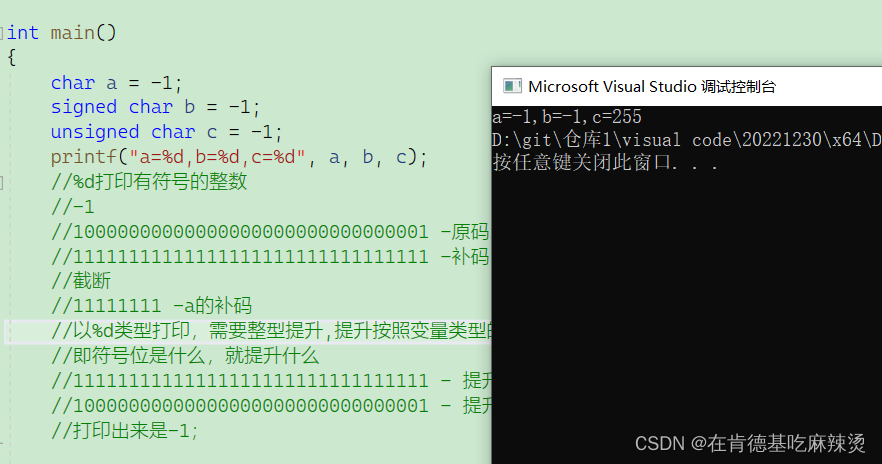
结果如上:
总结:整型提升时,
对于有符号数来说,提升时补的是符号位上的那个数。
对于无符号数来说,提升时补的是0。
再来一道例题:
int main()
{
char a = -128;
printf("%u\n", a);
}
打印出来的结果是什么呢?
写出-128的原码反码补码:
10000000000000000000000010000000 - 原码
11111111111111111111111101111111 - 反码
11111111111111111111111110000000 - 补码
存入a中,a是char类型,会发生截断,故a是10000000,
以%u的形式打印,%u打印的是无符号整数,故a会发生整型提升
a提升时,由于a是char类型,故提升补的是符号位上的数,补1
11111111111111111111111110000000 - a提升后的补码
%u打印无符号整数,故第一位不会被当成符号位。
对于无符号数来说,没有原码反码补码的概念,直接打印出来。
只有有符号数才有原码反码补码的概念。
所以打印出来的结果是一个很大的数字,使用计算机来计算一下结果
打印结果如下:
刚好符合预期
总结:对于无符号数来说,没有原码反码补码的概念
对于有符号数来说,正数的原码反码补码相同
负数的反码等于原码的符号位不变,其它位取反,补码等于反码+1。